Question

The quadrilateral, formed by joining the mid-points of the sides of a square, is a

Options

A. Rhombus
B. Square
C. Kite
D. Trapezium

Answer

B

Explanation

Given In a square ABCD, P, Q, R and S are the mid-points of AB, BC, CD and DA, respectively.

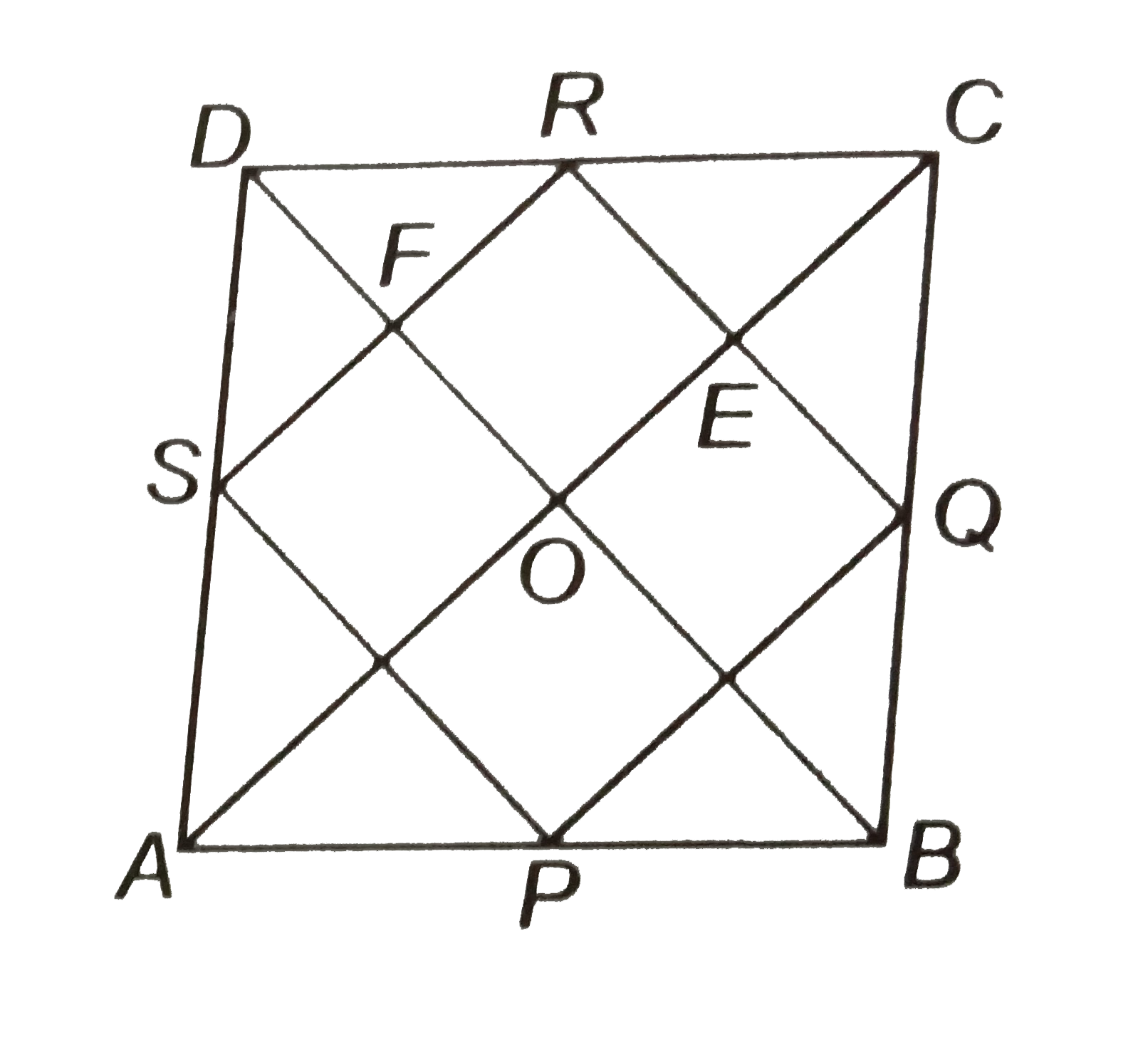
To show PQRS is a square.
Construction Join AC and BD.
Proof Since, ABCD is a square.
`therefore" "AB=BC=CD=AD`
Also, P, Q, R and S are the mid-points of AB, BC, CD and DA, respectively.
Then, in `Delta`ADC, `" "SR||AC`
and `" "SR=(1)/(2)AC" "`[by mid-point theorem]...(i)
In `Delta`ABC, `" "PQ||AC`
and `" "PQ=(1)/(2)AC" "...(iii)`
From Eqs. (i) and (ii), `" "SR||PQ and SR=PQ=(1)/(2)AC" "...(iii)`
Similarly, `" "SP||BD and BD||RQ`
`therefore" "SP||RQ and SP=(1)/(2)BD`
and `" "RQ=(1)/(2)BD`
`therefore" "SP=RQ=(1)/(2)BD`
Since, diagonals of a square bisect each other at right angle.
`therefore" "AC=BD`
`rArr" "SP=RQ=(1)/(2)AC" "...(iv)`
From Eqs. (iii) and (iv), `" "SR=PQ=SP=RQ" "`[all side are equal]
Now, in quadrilateral OERF,
`" "OE||FR and OF||ER`
`therefore" "angleEOF=angleERF=90^(@)`
Hence, PQRS is a square. `" "` Hence proved.