The quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rectangle, if

A

ABCD is a parallelogram

B

ABCD is a rectangle

C

diagonals of ABCD are equal

D

diagonals of ABCD are perpendicular to each other

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

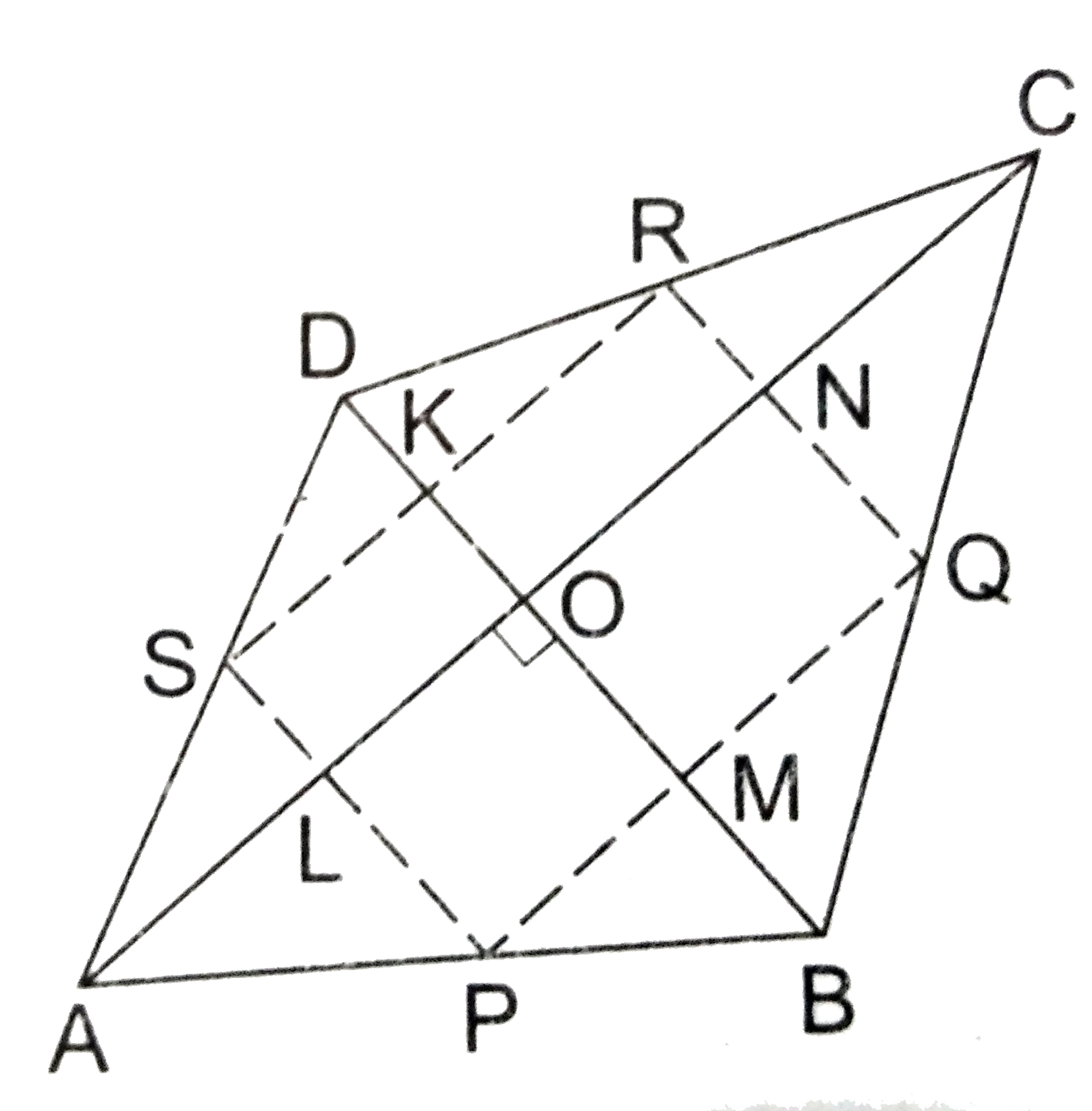
ocr_image
PQRS is always a parallelogram.
By midpoint theorem,
PS||BDandPQ||AC
⇒LP||OMandPM||LO⇒LPMO is a ||gm.
⇒∠LPM=∠LOM=90∘ [∵AC⊥BD(given)].
Now, PQRS is a ||gm with one angle ∠P=90∘ .
∴ PQRS is a rectangle if AC ⊥ BD. so ABCD is a rectangle

Updated on:21/07/2023
|
Class 9MATHSQUADRILATERALS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The quadrilateral formed by joining the mid-points of the sides of a quadrilateral PQRS, taken in order, is a rectangle, if

    APQRS is a rectangle
    BPQRS is parallelogram
    Cdiagonals of PQRS are perpendicular
    Ddiagonals of PQRS are equal

  • The quadrilateral formed by joining the midpoints of the sides of a quadrilateral ABCD, taken in order, is a rhombus, if

    AABCD is a parallelogram
    BABCD is a rectangle
    Cdiagonals of ABCD are equal
    Ddiagonals of ABCD are perpendicular to each other

  • The figure formed by joining the mid-points of the sides of a quadrilateral taken in order is

    Aparallelogram
    Brectange
    Csquare
    Dnone