D, E and F are the mid-points of the sides BC, CA and AB, respectively of and equilateral ΔABC. Show that ΔDEF is also an equilateral triangle.
Given In equilateral ΔABC, D, E and F are the mid-points of sides BC, CA and AB, respectively. ltBrgt To show ΔDEF is an equilateral triangle.
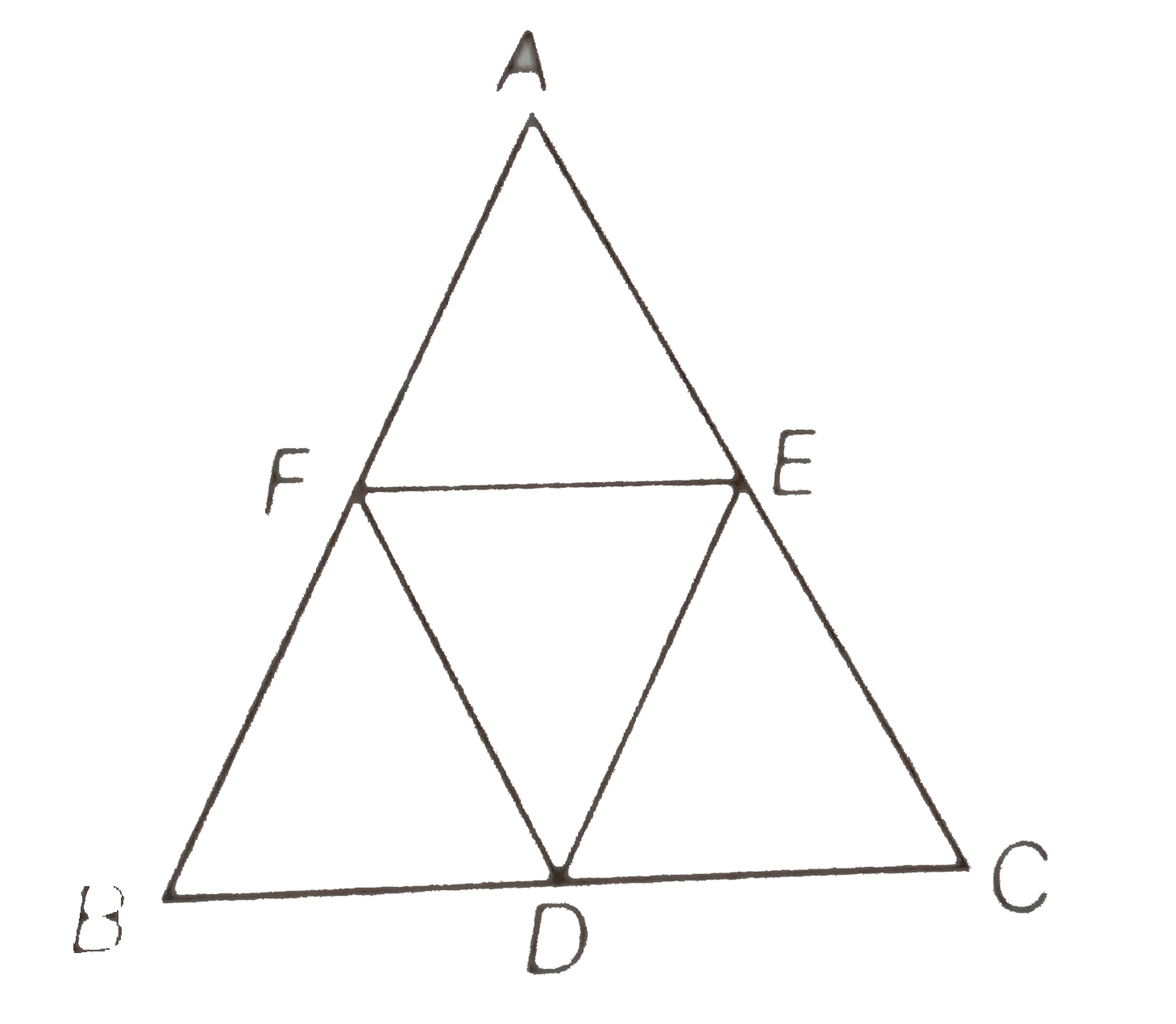
Proof Since in ΔABC, E and F are the mid-points of AC and AB respectively, then EF∣∣BC and
EF=12BC ...(i)
Similarly, DF||AC,DE||AB
and DE=12ABandFD=12AC [by mid-point theorem]...(ii)
since ΔABC is an equilateral triangle ltBrgt ∴ AB=BC=CA
⇒ 12AB=12BC=12CA [dividing by 2]
⇒ DE=EF=FD [from Eqs. (i) and (ii) ]
Thus, all sides of ΔDEF are equal.
Hence, ΔDEF is an equilateral triangle. Hence proved.
Topper's Solved these Questions
Similar Questions
In the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB of the equilateral ΔABC. Prove that ΔDEF is also an equilateral triangle.

View Solutionlf D, E and F are respectively the midpoints of the sides BC, CA and AB of an equilateral triangle ABC, prove that △DEF is also an equilateral triangle.
View Solution
Knowledge Check
Let D, E and F be the middle points of the sides BC,CA and AB respectively of a triangle ABC. Then, AD + BE + CF equals to
A0B0C2DNone of theseIn a ΔABC,D,E,F are the mid -points of the sides BC, CA and AB respectively, the vector AD is equal to
A−−→BE+−−→CFB−−→BE−−−→CFC−−→CF−−−→BED−−−→BE−−−→CFIf D, E and F are the mid-points of sides BC, CA and AB respectively of △ABC, then the ratio of the areas of △DEF to the area of △ABC is :
A1:4B1:2C1:3D2:3
In Figure, D,E and F are, respectively the mid-points of sides BC,CA and AB of an equilateral triangle ABC . Prove that DEF is also an equilateral triangle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC

View SolutionIn the adjoining figure D, E and F are the mid - points of the sides BC, AC and AB respectively to triangle. Show that ∠EDF=∠A, ∠DEF=∠B and ∠DFE=∠C:

View SolutionThevertices of a triangle ABC are A(−7,8),B(5,2)andC(11,0). If D, E, F are the mid-points of the sides BC,CAandAB respectively, show that ΔABC=4ΔDEF.
View Solution