Question

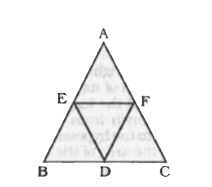
In Figure, ${\displaystyle D,E}$
and ${\displaystyle F}$
are, respectively the mid-points of sides ${\displaystyle BC,CA}$
and ${\displaystyle AB}$
of an equilateral triangle ${\displaystyle ABC}$
. Prove that ${\displaystyle DEF}$
is also an equilateral triangle.

Explanation

`"Proof: As ABC is an equilateral triangle

`therefore AB=BC=AC`-(1)

By midpoint theorem:

`EF=1/2 BC `

`DF=1/2 AC`

`DE=1/2 AB`

`therefore 1/2 AB=1/2 AC=1/2 BC`

`therefore EF=DF=ED`

Since all the sides of `/_\DEF` are equal, DEF is an equilateral triangle