ABCD is a square E,F,GandH are points on AB,BC,CDandDA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.

Given: AE=BF=CG=DH
∴BE=CF=DG=AH
In△AEHand△BEF
⇒AE=BF(Given)
⇒∠A=∠B(equal to 900)
⇒AH=BE
∴△AEH≅△BEF(By SAS criterion of congruency)
⇒∴∠AEH=∠EFB & ∠AHE=∠BEF(corresponding parts of Congruent Triangles)
∠AEH+∠AHE=900 & ∠EFB+∠BEF=900(∠A=∠B=900)
∠AEH+∠EFB+∠AHE+∠BEF=900+900=1800
∠AEH+∠BEF+∠AEH+∠BEF=1800
2(∠AEH+∠BEF)=1800
∠AEH+∠BEF=18002=900
∴∠HEF=1800−900=900
∴∠F=∠G=∠H=∠900
Since all the angles of EFGH are right angled and all sides are equal, EFGH is a square
Topper's Solved these Questions
Similar Questions
ABCD is a square E, F, G and H are points on AB, BC, CD and DA respectively, such that AE=BF=CG=DH. Prove that EFGH is square.
View SolutionABCD is a parallelogram. E is a point on BA such that BE=2 EA and F is a point on DC such that DF=2 FC. Prove that AE CF is a parallelogram whose area is one third of the area of parallelogram AB CD.
View SolutionABCD is a parallelogram, E and F are the mid-points of AB and CD respectively. GH is any line intersecting AD, EF and BC at G, P and H respectively. Prove that GP=PH
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(EBG)=ar(EFC)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that : ar(ADEG)=ar(GBCE) ar(EGB)=16ar(ABCD)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE andF is the point of BC such that BF=2FC. Prove that: ar(ADEG)=ar(GBCE)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: ar(EFC)=12ar(EBF)
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: arEGB=16ar(ABCD)
View Solution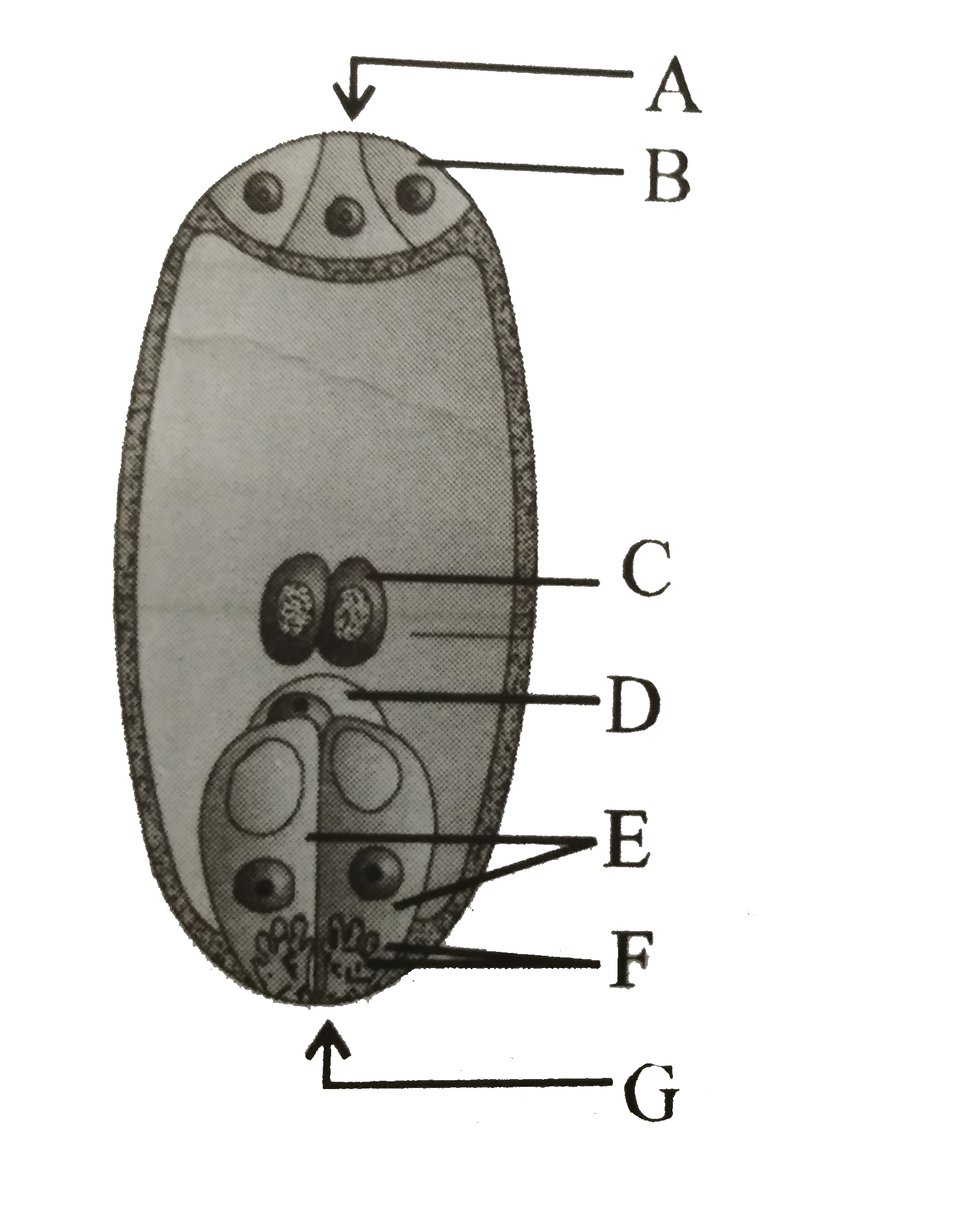
Identify A, B, C, D, E, F,G
View SolutionABCD is a parallelogram, G is the point on AB such that AG=2GB ,E is a point of DC such that CE=2DE and F is the point of BC such that BF=2FC. Prove that: Find what portion of the area of parallelogram is the area of EFG
View Solution
