Through A, B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC, CA and AB of a ΔABC as shown in figure. Show that BC=12QR.
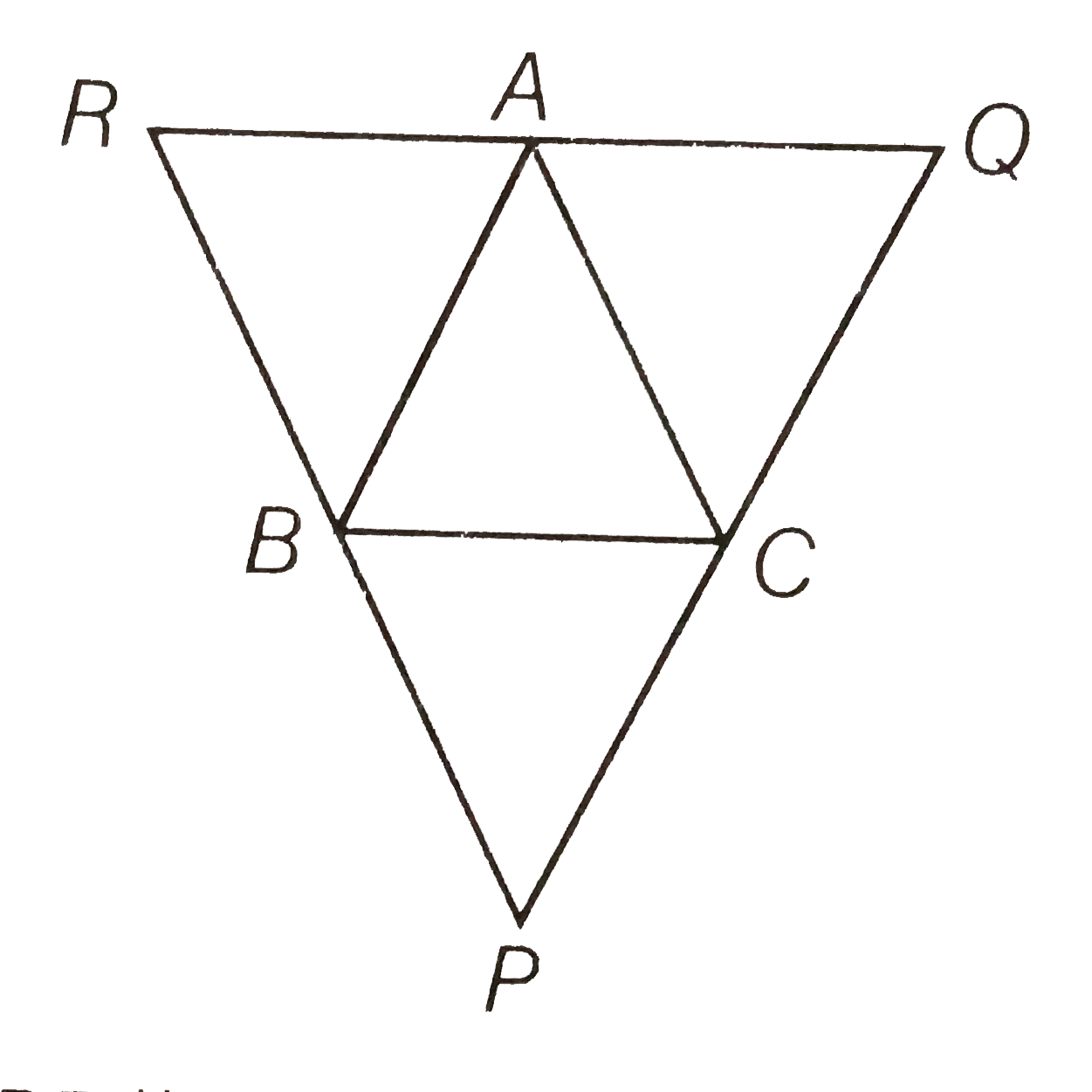
Given In ΔABC, PQ ∣∣ AB and PR ∣∣ AC and RQ ∣∣ BC.
To show BC=12QR
Proof In qudrilateral BCAR, BR||CAandBC||RA
So, quadrilateral, BCAR is a parallelogram.
∴ BC=AR ...(i)
Now, in quadrilateral BCQA, BC∣∣AQ
and AB∣∣QC
So, quadrilateral BCQA is a parallelogram,
∴ BC=AQ ...(ii)
On adding Eqs. (i) and (ii), we get
2BC=AR + AQ
⇒ 2BC=RQ
⇒ BC=12QR
Hence proved.
Topper's Solved these Questions
Similar Questions
Throuth A,B and C lines RQ, PR and QP have been drawn, respectively parallel to sides BC. CA and AB of a ΔABC as shown in the given figure. Show that BC=12QR.
View SolutionGiven ΔABC, lines are drawn through A,BandC parallel respectively to thesides BC,CAandAB, forming ΔPQR (Fig. 13.27). Show that BC=12QR.
View Solution
Knowledge Check
If D,E and F are respectively the midpoint of the sides BC,CA and AB of a ΔABC and the area of ΔABC=36cm2 , then area of ΔDEF is -----
A12cm2B9cm2C18cm2D8cm2
P is a point on the side BC of a triangle ABC such that AB=AP. Through AandC, lines are drawn parallel to BCandPA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
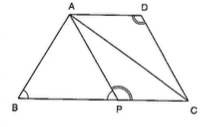
View SolutionP is a point on the side BC of a triangle ABC such that AB=AP. Through A and C, lines are drawn parallel to BC and PA, respectively, so as to intersect at D as shown in Figure. Show that ABCD is a cyclic quadrilateral.
View SolutionP,Q and R are, respectively, the mid-points of sides BC,CA and AB of a triangle ABC , PR and BQ meet at X.CR and PQ meet at Y . Prove that XY=14BC.
View SolutionThe sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and the median PM of triangle PQR respectively. Prove that the triangles ABC and PQR are congruent.
View SolutionIn the given figure points A, B, C respectively lie on sides OP, OQ such that AB||PQandAC||PR show that BC∣∣QR
View SolutionLet →a,→b,→c form sides BC,CA and AB respectively of a triangle ABC then
View SolutionTwo sides AB and BC and median AM of one triangle ABC are respectively equal to sides PQ and QR and median PN of ΔPQR (see figure). Show that

ΔABM≅ΔPQN
View Solution
