ABCD is a trapezium in which AB ∣∣ DC, BD is a diagonal and E is the mid-point of AD. A line is drawn through E parallel to AB intersecting BC at F (see Fig. 8.30). Show that F is the mid-point of BC.
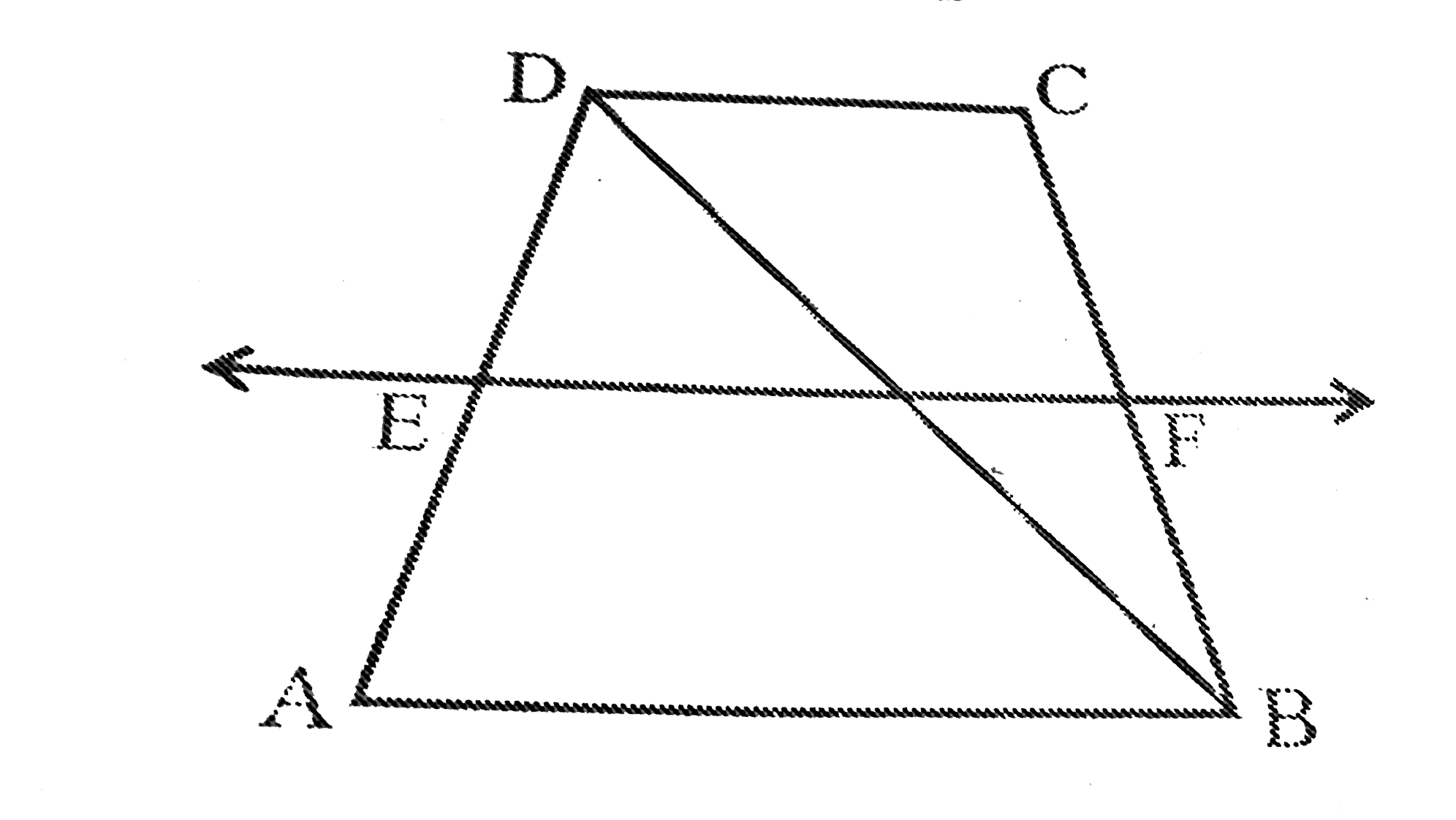
∠ABD
AE=ED
EG||AB
G is midpoint
∴DG=GB
∠DBC
DG=GB
EF||DC
GF||DC
F is midpoint
∴FB=FC.
Topper's Solved these Questions
- QUADRILATERALSBOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - EXERCISE 8.1
12 Videos
- QUADRILATERALSBOOK - NCERTCHAPTER - QUADRILATERALSEXERCISE - SOLVED EXAMPLES
8 Videos
- PROBABILITYBOOK - NCERTCHAPTER - PROBABILITYEXERCISE - SOLVED EXAMPLES
10 Videos
- STATISTICSBOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 14.1
2 Videos
Similar Questions
ABCD is a trapezium with AB || DC. E is midpoint of side AD. From point E a line is drawn parallel to AB that intersects BC at F. Show that F is midpoint of BC.
View SolutionAB and CD are the parallel sides of a trapeziuml. E is the mid-point of AD. A line through E and parallel to side AB meets the line BC at point F. Prove that F is the mid-point of BC.
View Solution
Knowledge Check
ABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2In a trapezium ABCD, AB is parallel to CD. If E is midpoint of side AD and a line drawn from point E, parallel to the parallel sides cuts BC at F then
ABF = CF if AD = BCBBF = CF ia always trueCBF:CF is less than 1 if AD<BCDBF:CF is greater than 1 if AD>BCE is the mid-point of the side AD of the trapezium ABCD with AB∣∣DC. A line through E drawn parallel to AB intersects BC at F. then
APoint F trisect BCBPoint F bisect BCCAB=CDDNone
ABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:

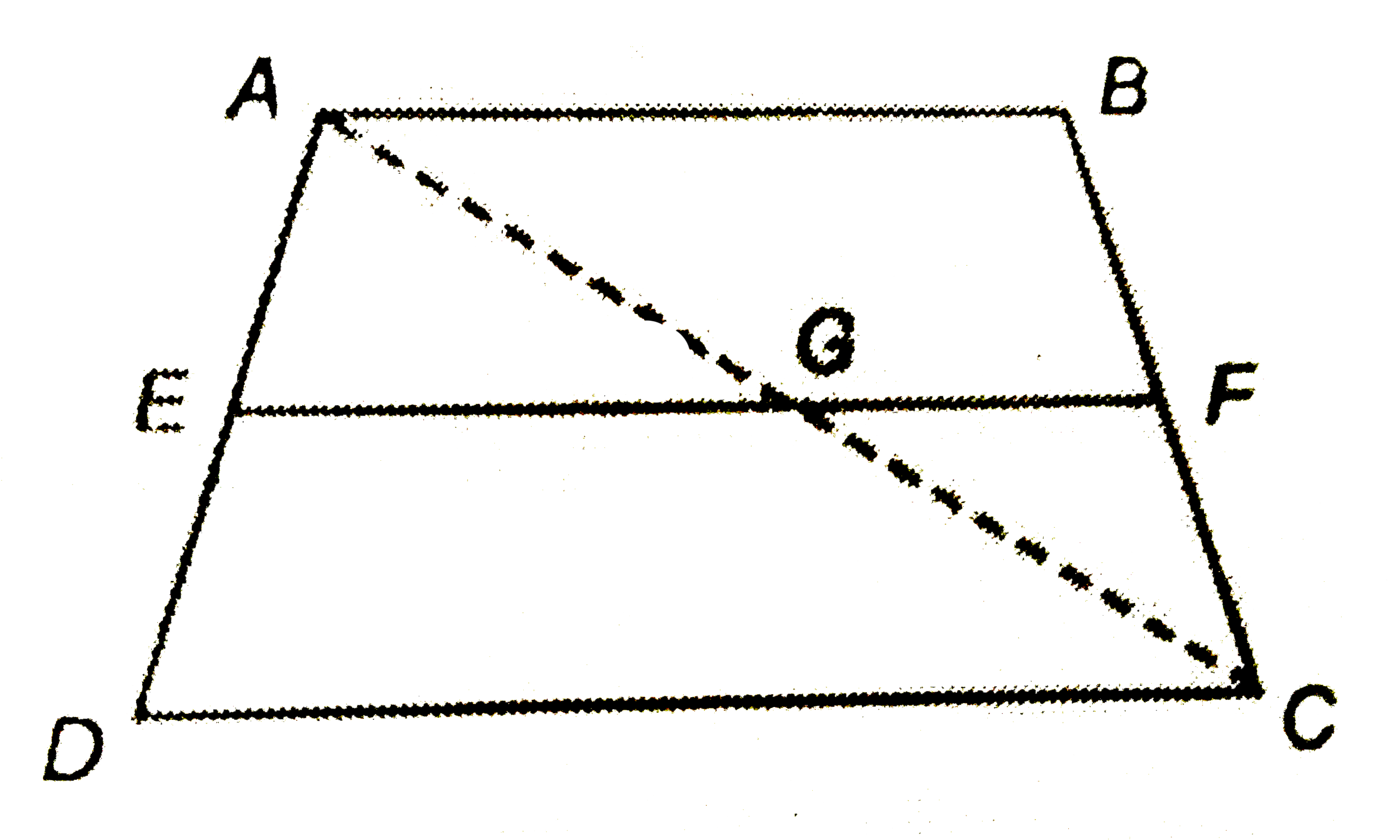
View SolutionIn Figure, ABCD isa trapezium in which side AB is a parallel to side DC and E is the mid-point of side AD. If F is a point on the side BC such that the segment EF is parallel to side DC . Prove that F is the mid point of BC and EF=12(AB+DC).
View SolutionIn the figure ABCD is a trapezium in which side AB is parallel to side DC and E is the midpoint of side AD. If F is a point on the side BC such that the line segment EF is parallel to DC.Prove that Fis the mid-point of BC and EF=12(AB+DC)
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
View SolutionABC is a triangle right-angled at C. A line through the mid-point M of hypotenuse AB and parallel to BC intersects AC at D. Show that
(i) D is the mid-point of AC
(ii) MD⊥AC
(iii) CM = MA=12AB
View Solution
