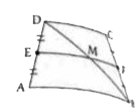
In the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
Video Solution
Text Solution
Join AC which interests EF at G.
In △ADC, EG||DC
and E is the mid-point of AD
then G is mid-point of AC (converse of mid-point theorem)
Again, E is mid point of AD.
Since, G is mid-point of AC,
EG=12DC (mid point theorem)...(1)
Now, EF"||" AB
EF"||"AB
In △CAD,
Since, G is mid-point of CA,
and GF||AB (becuaseEF||AB)
∴ F is mid point of CB. (converse of mid-point theorem)
In △CAB,
Since, F is mid point of CB.
and G is mid-point of CA.
∴GF=12AB (mid-point theorem)...(2)
Adding (1) and (2), we get
EG+GF=12(CD+AB)
⇒ EF=12(AB+CD) Hence proved.
|
Topper's Solved these Questions
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Problems From NCERT/exemplar
Explore 11 Videos
- QUADRILATERALSBook:NAGEEN PRAKASHANChapter:QUADRILATERALSExercise:Exercise 8a
Explore 29 Videos
- PROBABILITYBook:NAGEEN PRAKASHANChapter:PROBABILITYExercise:Revision Exercise (very Short Answer /short Answer Questions)
Explore 10 Videos
- STATISTICSBook:NAGEEN PRAKASHANChapter:STATISTICSExercise:Revision Exercise
Explore 10 Videos
Similar Questions
Knowledge Check
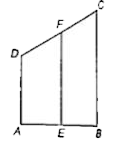
In figure, ABCD is a trapezium in which AB I I DC. Find the length of DC.
 A17 cmB11 cmC13 cmD15 cm
A17 cmB11 cmC13 cmD15 cmABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
A(AD+BC)2B(AB+CD)2C(DF xx CF)/(AE xx BE)DAD+EF+BC2
In the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠A=∠B

View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
∠C=∠D

View SolutionIn the given figure ABCD is a trapezium in which AB∣∣DC and AB:DC=3:2, The ratio of the areas of △AOB and △COD is
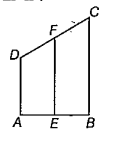
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
diagonal AC = diagonal BD

View SolutionIn the given figure ABCD is a trapezium with AB || Dc and AD = BC prove that
ΔABC≈ΔBAD

View Solution