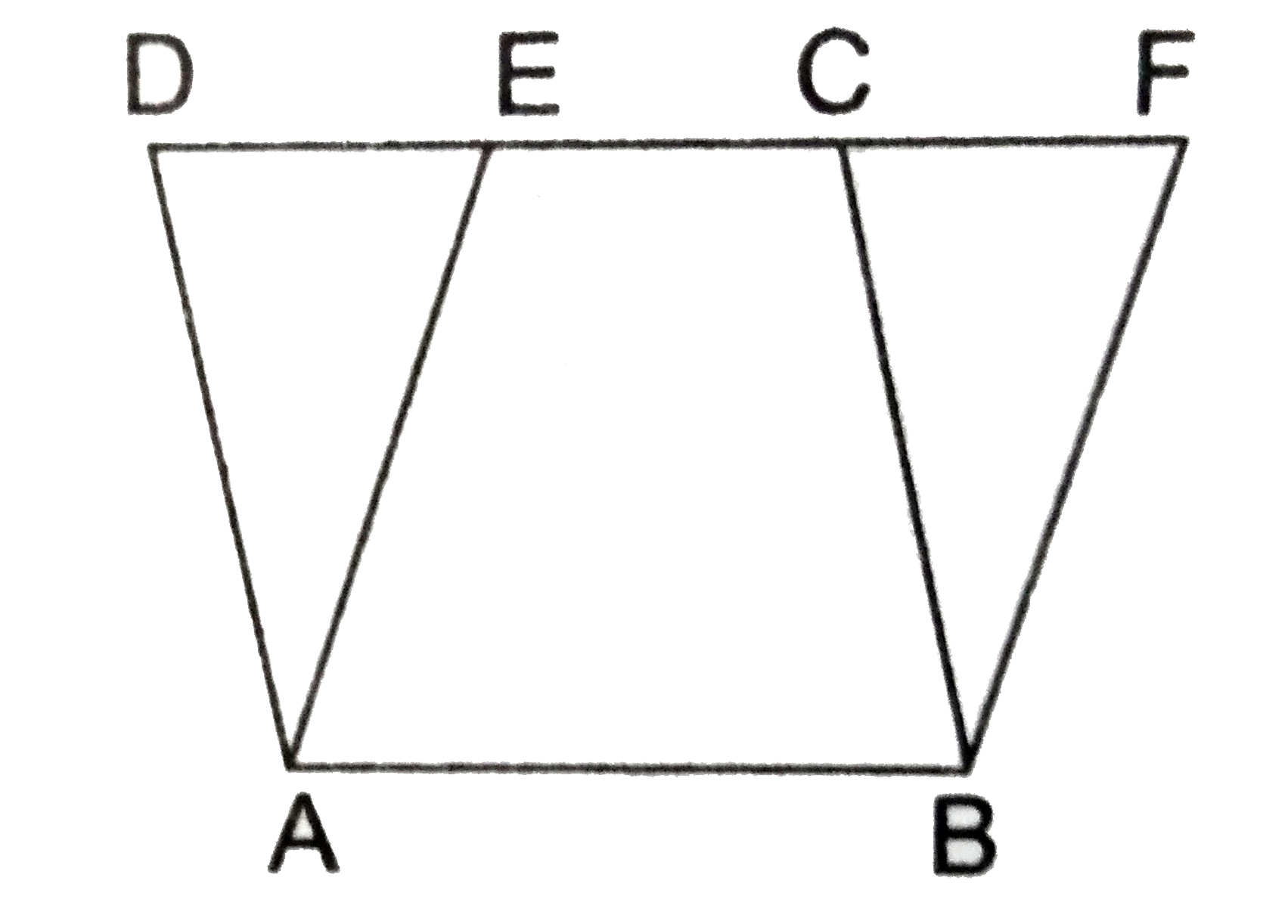
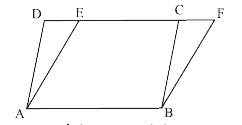
In the given figure, ABCD and ABEF are parallelograms such that ar(quad. EABC) 17cm2 and ar(||gm ABCD) =25cm2. Then ar(△BCF) = ?
A
4cm2
B
4.8cm2
C
6cm2
D
8cm2
Video Solution
Text Solution
The correct Answer is:D
||gm ABCD and ||gm ABFE being on the same base and between the same parallels,
we have:
ar(||gm ABFE)=ar(||gm ABCD)=25 cm2.
ar(△BCF)=ar(||gm ABFE)−ar(quad. EABC)=(25−17)cm2=8cm2.
|
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
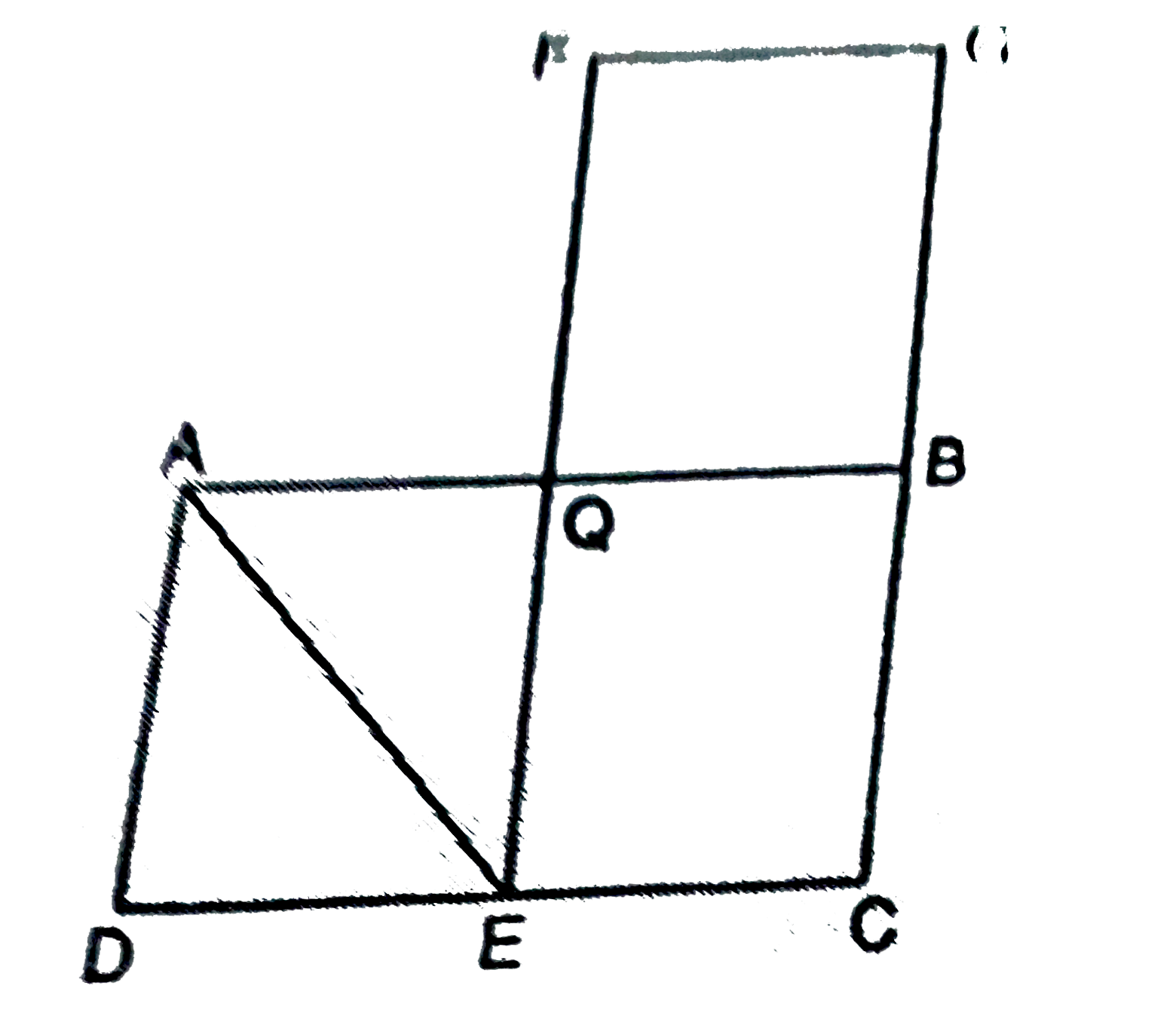
In the given figure, ABCD and AEFD a re two parallelograms.
ar(ΔPEA) =Aar(∣∣gmΔPEA)Bar(ΔPFD)Car(ΔQFD)Dar(∣∣gmΔCQPB)In the given figure, ABCD and AEFD a re two parallelograms.
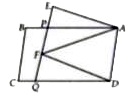
(ar(ΔAPE))/(ar(ΔPFA)) =A(ar(ΔQFD))/(ar(ΔPFD))B(ar(ΔAEF))/(ar(ΔPFD))C(ar(ΔQFD))/(ar(ΔAEF))DNone of theseIn the given figure, a ||gm ABCD and a rectangle ABEF are of equal area. Then,
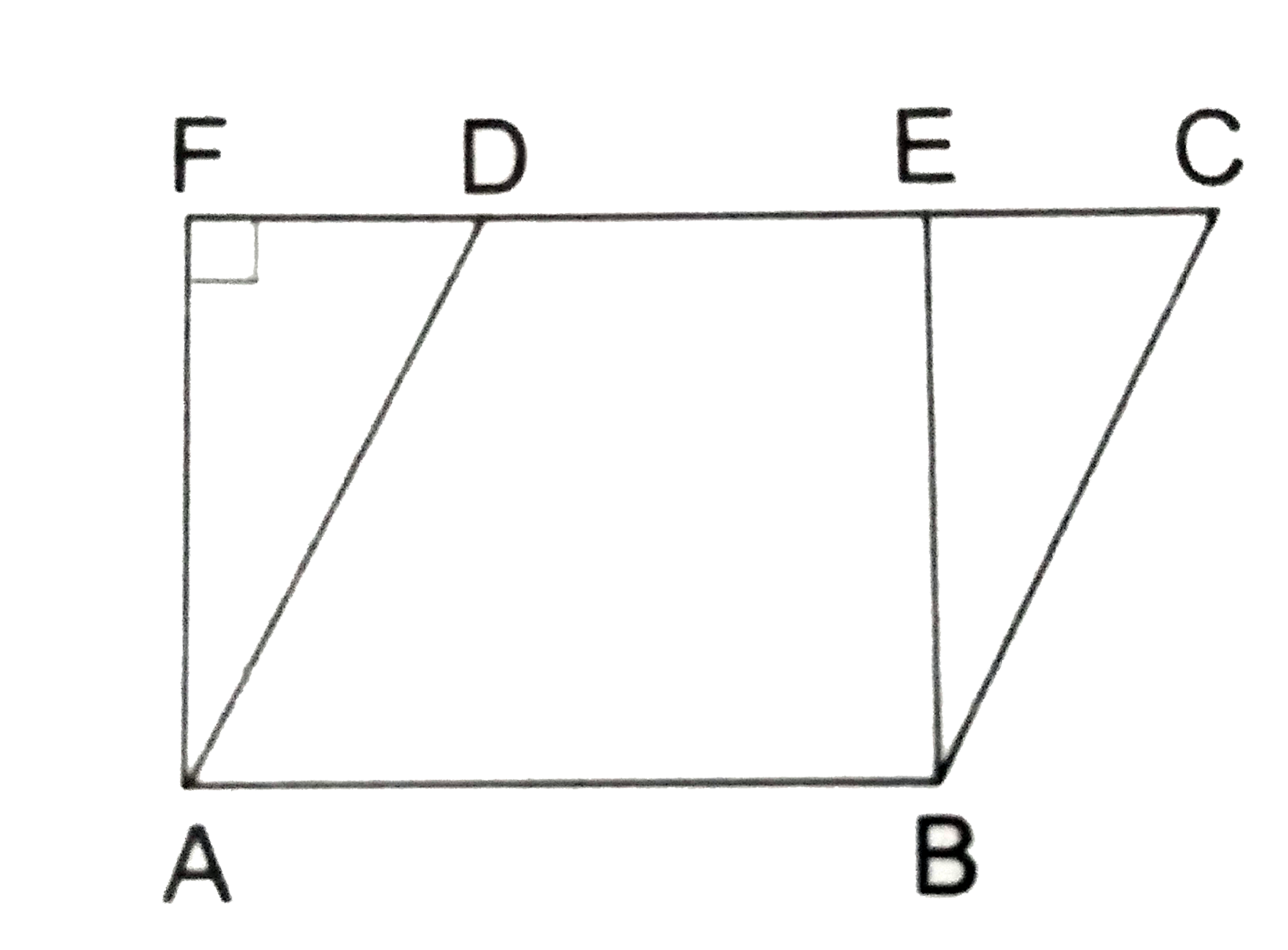 Aperimeter of ABCD = perimeter of ABEFBperimeter of ABCD < perimeter of ABEFCperimeter of ABCD > perimeter of ABEFDperimeter of ABCD =12 perimeter of ABEF
Aperimeter of ABCD = perimeter of ABEFBperimeter of ABCD < perimeter of ABEFCperimeter of ABCD > perimeter of ABEFDperimeter of ABCD =12 perimeter of ABEF
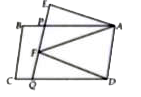
In the figure ABCD and ABFE are Parallelograms then find ar (ΔBCF).
If ar (ABCE)=18cm2
ar (ABCD)=25cm2
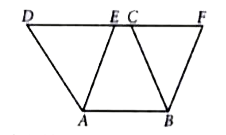
View SolutionIn the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
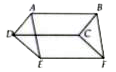
View SolutionIn Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
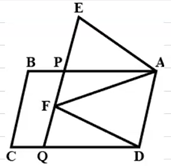
View SolutionIn figure, ABCD and AEFD are two parallelograms. Prove that ar(ΔPEA)=ar(ΔQFD).
View Solution