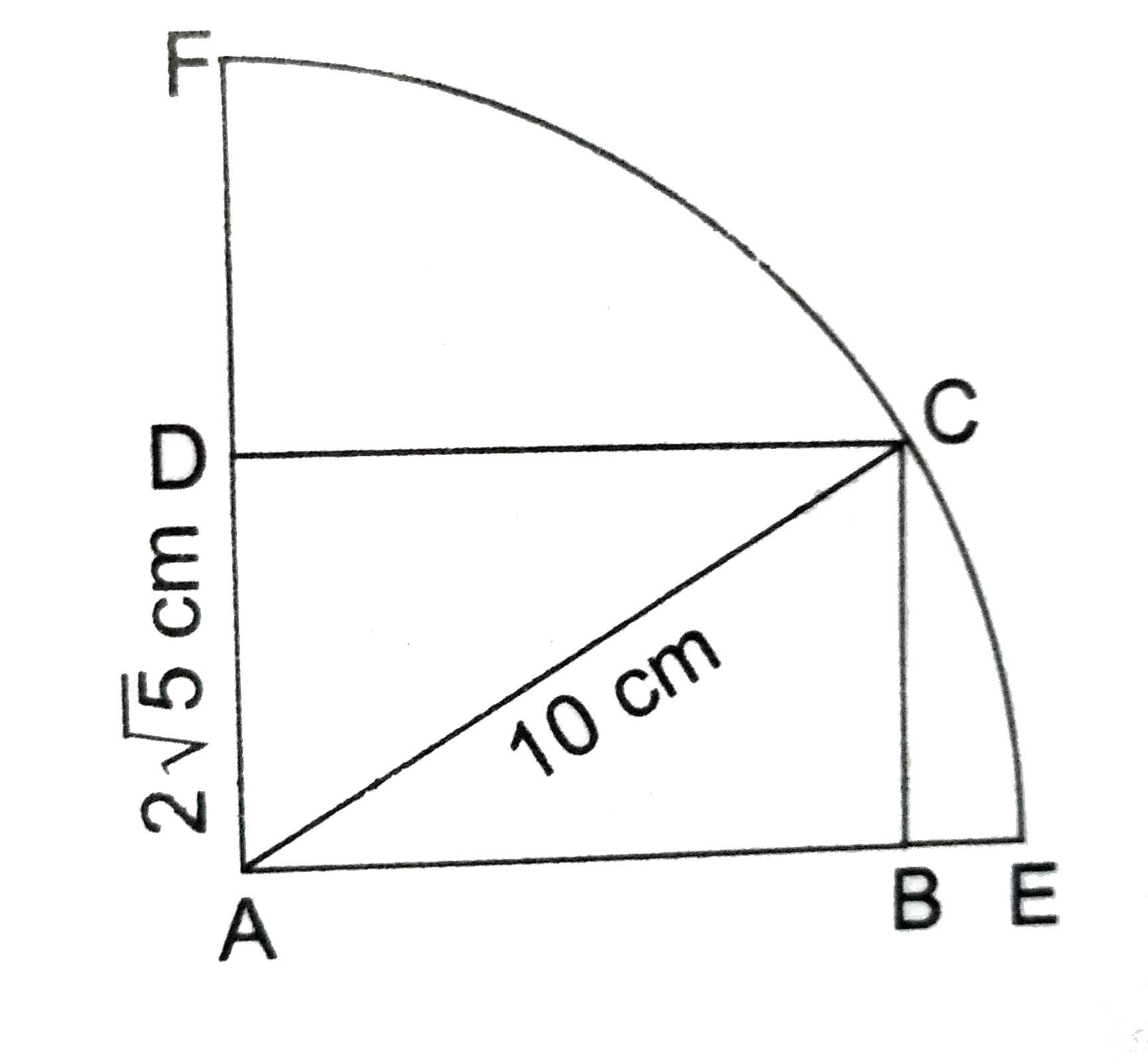
In the given figure, ABCD is a rectangle inscribed in a quadrant of a circle of radius 10 cm. If AD=√25 cm then area of the rectangle is
32cm2
40cm2
44cm2
48cm2
The correct Answer is:B
AB2=AC2−BC2=(AC2−AD2)={(102)−2(√5)2}=(100−20)=80
⇒AB=√80=√16×5=4√5cm.
∴ar(rect. ABCD)=(AB×AD)=(4√5×2√5)cm2=40cm2
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - ASSERTION & REASON TYPE
5 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
PQRS is a rectangle inscribed in a quadrant of a circle of radius 13 cm and A is any point on PQ. If PS = 5 cm, then ar (ΔPAS)=.
A32.5cm2B30cm2C35cm2D12.5cm2The maximum area of rectangle, inscribed in a circle of radius 'r', is :
Aπr2Br2C2r2D14πr2
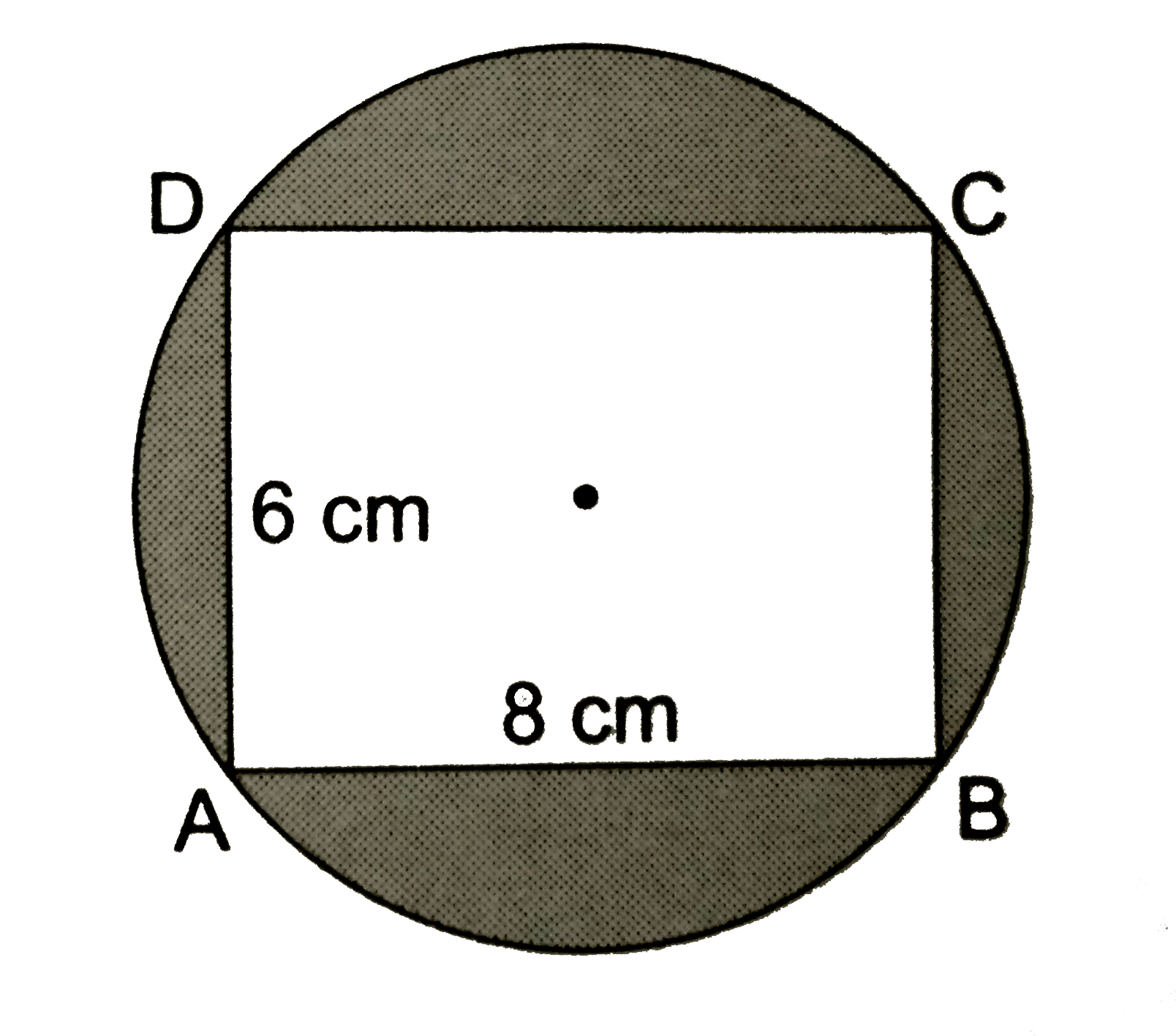
In the given figure ABCD is a rectangle inscribed in a circle having length 8 cm and breadth 6 cm. If π=3.14 then the area of the shaded region is
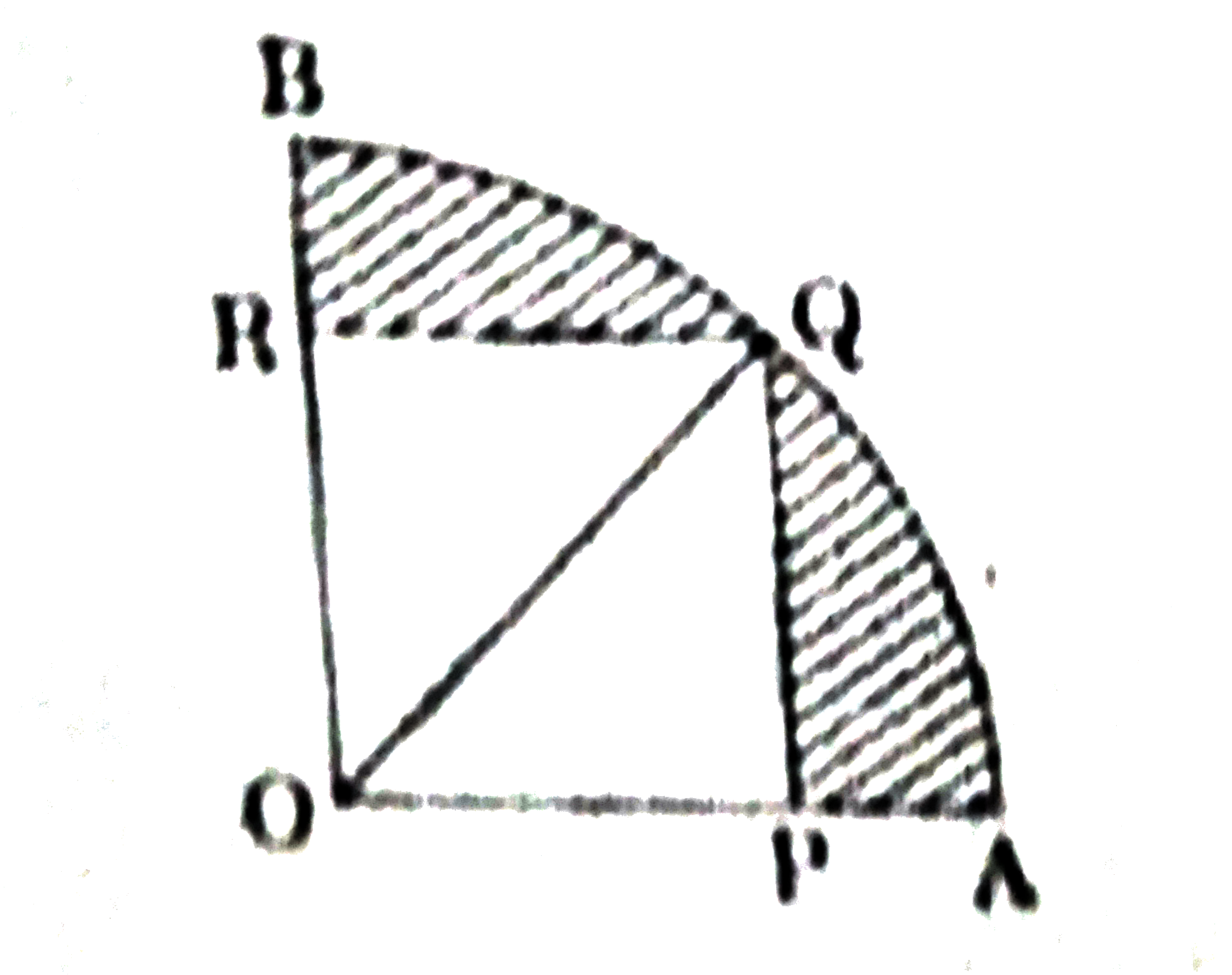
View SolutionIn Figure , a square OPQR is inscribed in a quadrant OAQB of a circle. If the radius of circle is 6√2 cm, find the area of the shaded region
View SolutionA reactangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle
View SolutionA rectangle in inscribed in a circle of radius 5 cm. if the breadth of the rectangle is 6 cm. then find the length of the rectangle.
View SolutionIn the given figure, ABCD is a square of side 7cm, DPBA and DQBC are quadrants of circles each of the radius 7 cm. Find the area of shaded region.
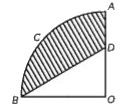
View SolutionIn figure, OACB is a quadrant of a circle with centre O and radius 7 cm. If AD = 2 cm, find the area of the shaded region.
View Solution