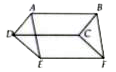
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
In parallelogram, ABCD, AD=BC
In parallelogram, DCFE, DE=CF
In parallelogram, ABFE, AE=AF
Now, in ΔADE and ΔBCF
AD=BC
DE=CF
AE=AF
So, from SSS criterion, ΔADE≅ΔBCF
As these two triangles are congruent, their areas will be equal.
ar(ADE)=ar(BCF)
Similar Questions
In Fig. 9.31, ABCD, DCFE and ABFE are parallelograms. Show that ar(ADE)=ar(BCF).
View SolutionIn the figure, ABCD, DCFE and ABFE are parallelograms. Show that ar(ΔADE) = ar(ΔBCF).
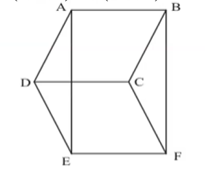
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
View SolutionIn Figure, ABCDandAEFD are two parallelograms? Prove that: ar(APE):ar(PFA)=ar(QFD):ar(PFD)
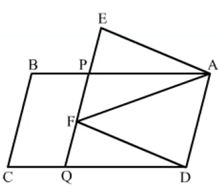
View SolutionIn Figure ABCDandAEFD are two parallelograms. Prove that: PE=FQ

View SolutionABCD and APQR are two parallelograms. Prove that ∠C=∠Qand∠B=∠R
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
View SolutionXY isa line parallel to side BC of ABC.BEA and CFAB meet XY in E and F respectively.Show that ar(ABE)=ar(ACF).
View SolutionIn a parallelogram ABCD,E,F are any two points on the sides AB and BC respectively. Show that ar(ADF)=ar(DCE).
View Solution
