Question

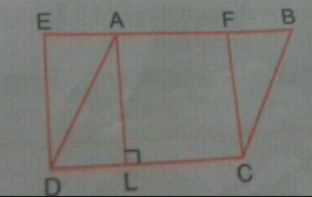
$\text{ABCD}$ is a parallelogram and $\text{EFCD}$ is a rectangle. Also, $AL\perp DC$. Prove that:
(i) $ar\left(ABCD\right)=ar\left(EFCD\right)$
(ii) $ar\left(ABCD\right)=DC\times AL$

Explanation

To solve the problem, we need to prove two statements about the areas of the parallelogram $$ABCD$$ and the rectangle $$EFCD$$.

Given:
- $$ABCD$$ is a parallelogram.
- $$EFCD$$ is a rectangle.
- $$AL\perp DC$$ (meaning $$AL$$ is perpendicular to $$DC$$).

To Prove:
1. $$\text{Area}\left(ABCD\right)=\text{Area}\left(EFCD\right)$$
2. $$\text{Area}\left(ABCD\right)=DC\times AL$$

1. Identify the bases and heights:
- In parallelogram \(ABCD\), the base can be taken as \(CD\) and the height is the perpendicular distance from point \(A\) to line \(CD\).
- In rectangle \(EFCD\), the base is also \(CD\) and the height is the perpendicular distance from point \(E\) to line \(CD\).

Hint: Identify the common base and the heights from the respective vertices to the base.

2. Use the property of parallelograms:
- According to the theorem, if two parallelograms lie on the same base and between the same parallels, their areas are equal.

Hint: Recall the theorem about the areas of parallelograms that share a base and are between the same parallels.

3. Conclusion for Part (i):
- Since both \(ABCD\) and \(EFCD\) share the base \(CD\) and lie between the same parallels (lines through \(AB\) and \(EF\)), we conclude:
\( \text{Area}(ABCD) = \text{Area}(EFCD) \)

Part (ii): Proving \( \text{Area}(ABCD) = DC \times AL \)

1. Area of parallelogram formula:
- The area of a parallelogram is given by the formula:
\( \text{Area} = \text{Base} \times \text{Height} \)
- Here, we can take \(DC\) as the base and \(AL\) as the height (since \(AL\) is perpendicular to \(DC\)).

Hint: Remember the formula for the area of a parallelogram and identify the base and height.

2. Substituting values:
- Therefore, we can write:
\( \text{Area}(ABCD) = DC \times AL \)

3. Conclusion for Part (ii):
- This shows that the area of parallelogram \(ABCD\) can also be expressed as the product of its base \(DC\) and height \(AL\):
\( \text{Area}(ABCD) = DC \times AL \)

Final Conclusion:
We have successfully proved both parts of the question:
1. \( \text{Area}(ABCD) = \text{Area}(EFCD) \)
2. \( \text{Area}(ABCD) = DC \times AL \)