D, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
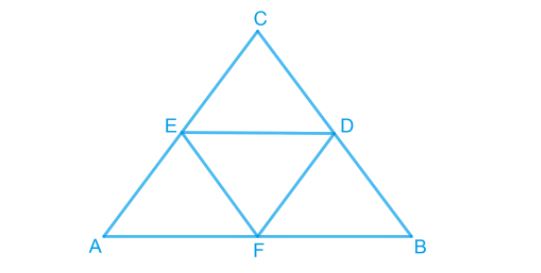
i) In ΔABC, D and E are the mid-points of side BC and AC respectively.
Therefore, the line joining points D and E will be parallel to line AB and also half of it as per the midpoint theorem.
The mid-point of AB is Fand E is the mid-point of AC
∴ ED ║AB and ED=12AB
Since ED║AB.
Therefore, ED║FB and ED=FB [F is the midpoint of AB]
Since one pair of the opposite side in quadrilateral BDEF is parallel and equal to each other, Therefore, BDEF is a parallelogram.
Similarly, we can prove, AEDF and CEFD are also parallelograms.
ii) Now, in parallelogram BDEF,
The diagonal DF of the parallelogram BDEF divides it into two triangles BDF and DEF of equal areas.
∴ ar(ΔDEF)=ar(ΔBDF)………..(i)
Similarly, DCEF is also parallelogram.
∴ ar(ΔDEF)=ar(ΔDEC)……….(ii)
Also,AEDF is a parallelogram.
∴ ar(ΔDEF)=ar(ΔAFE)……….(iii)
From equation (i), (ii) and (iii),
ar(ΔDEF)=ar(ΔBDF)=ar(ΔDEC)=ar(ΔAFE)……….(iv)
Now,
ar(ΔABC)=ar(ΔDEF)+ar(ΔBDF)+ar(ΔDEC)+ar(ΔAFE)……….(v)
ar(ΔABC)=ar(ΔDEF)+ar(ΔDEF)+ar(ΔDEF)+ar(ΔDEF) [Using (iv) & (v)]
ar(ΔABC)=4×ar(ΔDEF)
ar(ΔDEF)=14ar(ΔABC)
iii) ar(║gmBDEF)=ar(ΔBDF)+ar(ΔDEF)=ar(ΔDEF)+ar(ΔDEF)
ar(║gmBDEF)=2ar(ΔDEF)
ar(║gmBDEF)=2×14ar(ΔABC)
ar(║gmBDEF)=12ar(ΔABC)
Similar Questions
D, E and F are respectively the mid-points of the sides BC, CA and AB of aΔABC.Show that (i) BDEF is a parallelogram. (ii) ar (DEF)=14ar (ABC)(iii) ar (BDEF)=12ar (ABC)
View SolutionD, E and F are respectively the mid -points of the sides BC, CA and AB of a △ABC .Show that (i) BDEF is a parallelogram
View SolutionD, E and F are respectively the mid-points of the sides BC, CA and AB of a ΔABC. Show that
ar(BDEF) =12ar(△ABC)
View SolutionD, E and F are the mid-points of the sides BC, CA and AB of a triangle ABC. Show that
BDEF is a parallelogram
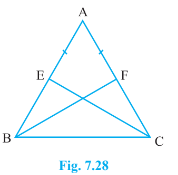
View SolutionE and F are respectively the mid-points of equal sides AB and AC of ΔABC(see Fig. 7.28). Show that BF = C E.
View SolutionIn the adjoining figure D, E and F are the mid-points of the sides BC, CA and AB respectively of ΔABC. Prove that:
(i) □BDEF is a parallelogram
(ii) area of ΔDEF=14× area of ΔABC
(iii) area of □BDEF=12× area of ΔABC

View SolutionE,F,G,H are respectively, the mid-points of the sides AB,BC,CD and DA of parallelogram ABCD . Show that the quadrilateral EFGH is a parallelogram and that its area is half the area of the parallelogram, ABCD. GIVEN : A quadrilateral ABCD in which L,F,G,H are respectively the mid-points of the sides AB,BC,CD and DA. TO PROVE : (i) Quadrilateral EFGH is a parallelogram ar(^(gm)EFGH)=12ar(^(gm)ABCD) CONSTRUCTION : Join AC and HF
View SolutionIf ABCD is a parallelogram, then prove that ar(△ABD)=ar(△BCD)=ar(△ABC)=ar(△ACD)=12ar(∣∣gmABCD)
View SolutionIn ΔABC, D, E and F are respectively the mid-points of sides AB, BC and CA. Show that ΔABCis divided into four congruent triangles by joining D, E and F.
View SolutionD, E, F are the mid-points of the sides BC, CA and AB respectively of a ABC . Determine the ratio of the areas of DEF and ABC .
View Solution
