The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed. Show that ar (ABCD) = ar (PBQR).
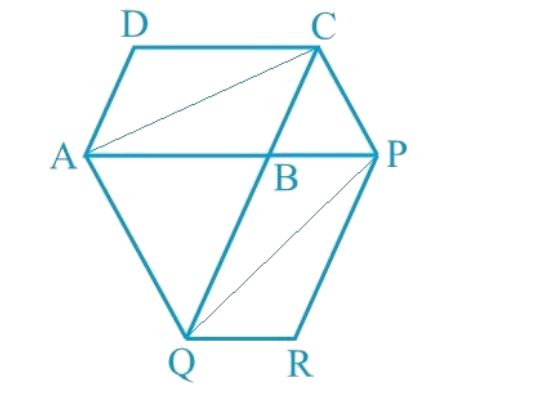
ΔACQ and ΔAQP are lying on the same base AQ and exist between the same parallels AQ and CP.
Two triangles on the same base (or equal bases) and between the same parallels are equal in area.
Area(ΔACQ)=Area(ΔAPQ)
Subtracting ar(ΔABQ) on both sides.
ar(ΔACQ)−ar(ΔABQ)=ar(ΔAPQ)−ar(ΔABQ)
ar(ΔABC)=ar(ΔQBP)... (1)
Since AC and PQ are diagonals of parallelograms ABCD and PBQR respectively,
Therefore, ar(ΔABC)=12ar(ABCD)... (2)
Similarly, ar(ΔQBP)=12ar(PBQR)... (3)
From Equations (1), (2), and (3), we obtain
12ar(ABCD)=12ar(PBQR)
ar(ABCD)=ar(PBQR)
proved.
Similar Questions
The side AB of a parallelogram ABCD is produced to any point P. A line through A parallel to CP meets CB produced in Q and the parallelogram PBQR completed. Show that ar(^(gm)ABCD)=ar(^(gm)BPRQ). CONSTRUCTION : Join AC and PQ. TO PROVE : ar(^(gm)ABCD)=ar(^(gm)BPRQ)
View SolutionThe side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(∣∣gmABCD)=ar(∣∣gmPBQR)
View Solution
Knowledge Check
In a parallelogram ABCD, a side AB is extended to E such that BE = AB. If DE cut the line BC at Q then point Q divide BC in what ratio?
A1:2B1:1C2:3D2:1
The side AB of a parallelogram ABCD is produced to any point P. A line through A and parallel to CP meets CB produced at Q and then parallelogram PBQR is completed as shown in Figure. Show that ar(^(gm)ABCD)=argmPBQR).

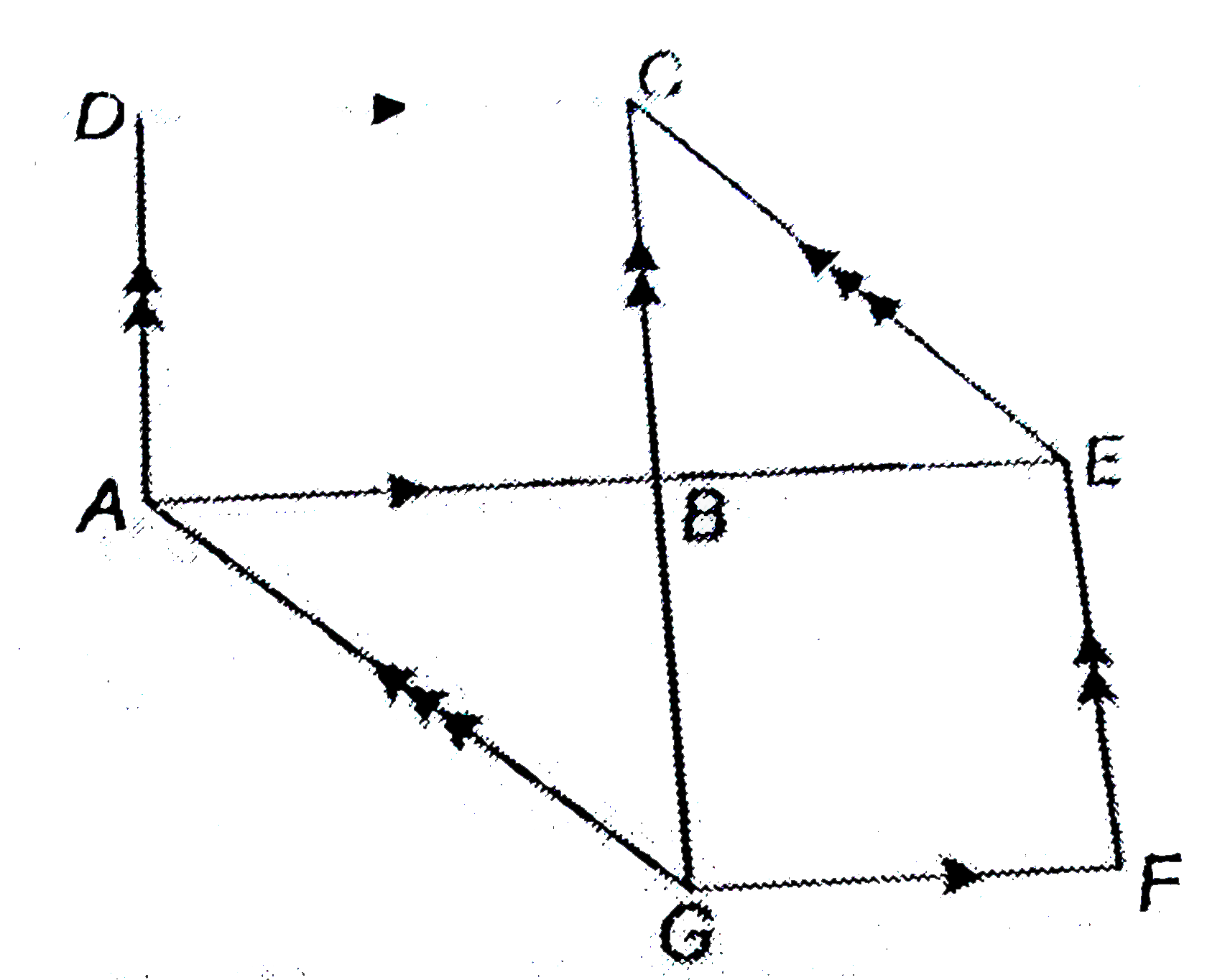
View SolutionThe side AB of a parallelogram ABCD is produced to any point E. A line through A and parallel to CE meets CB produced at G and then parallelogram EBGF is completed (see the figure). Prove that
area of ||gmABCD= area of ||gmBEFG.
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A Line through B parallel to PD meets DC at Q and AD produced at R . Prove that (i) AR=2BC (ii) BR=2BQ.
View SolutionIn Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F. Show that: ar (ACB)=ar (ACF) ar (AEDF)=ar (ABCDE)
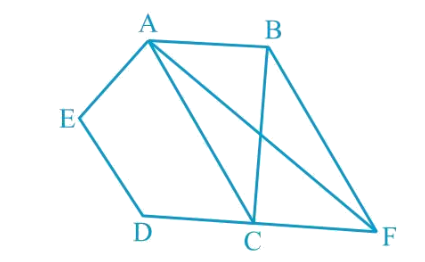
View Solutionp AND q are any two points lying on the sides DC and AD respectively of a parallelogram ABCD. Show that ar(APB)=ar (BQC).
View SolutionP is the mid-point of side AB of a parallelogram ABCD . A line through B parallel to PD meets DC at Q and AD produced at R. Prove that: AR=2BC (ii) BR=2 BQ
View Solution
