समांतर चतुर्भुज ABCD की भुजा AB को किसी बिंदु P तक बढ़ाया गया है। बिंदु A से CP के समांतर खींची गयी रेखा CB के आगे बढ़ाये गये भाग को Q पर मिलती है। और समांतर चतुर्भुज PBQR को पूरा करती है। सिद्ध कीजिए कि
$a r ({।।}^{g m} A B C D) = a r ({।।}^{g m} B P R Q)$

Video Solution

Text Solution

Verified by Experts

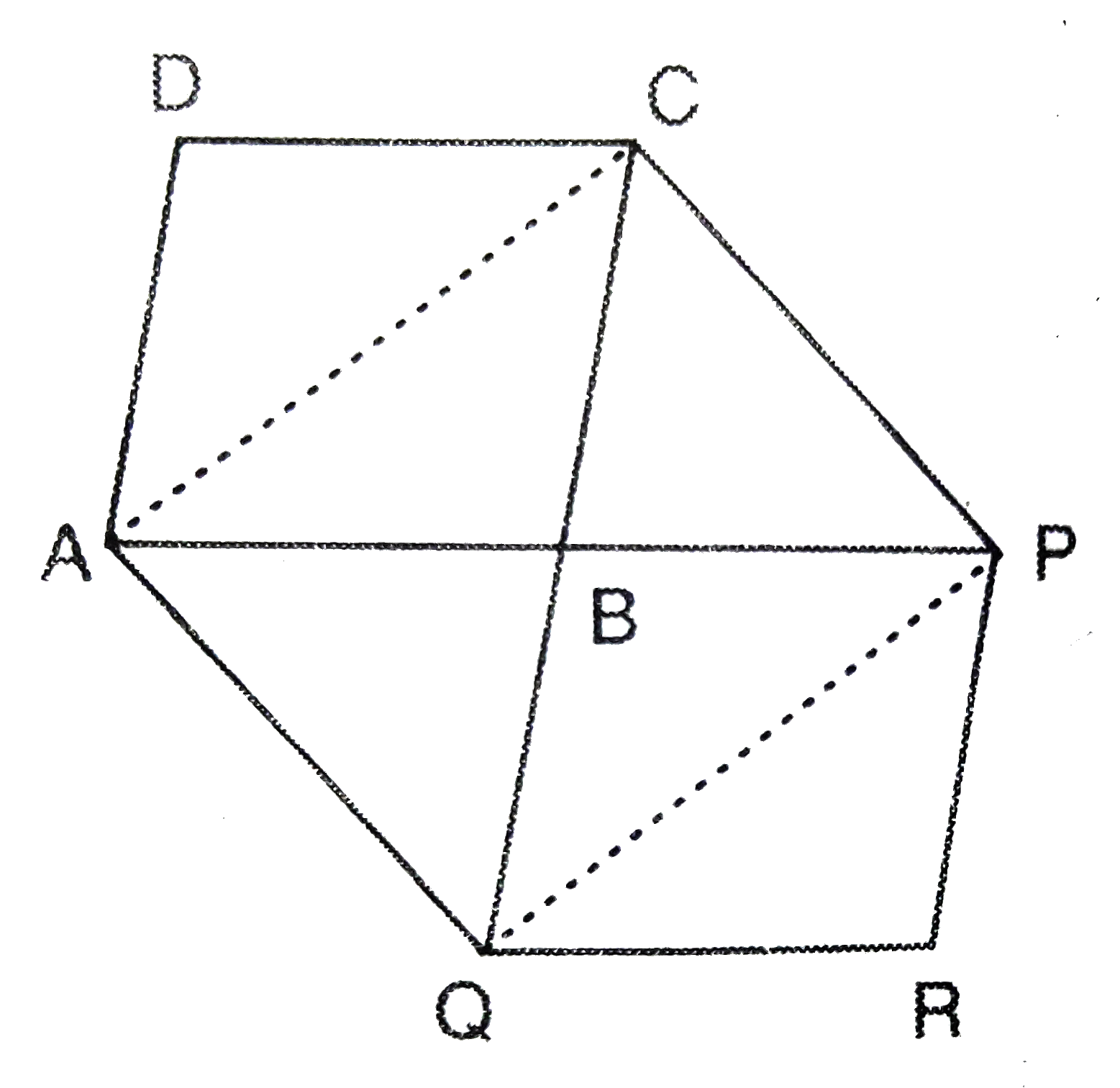
रचना : AC तथा PQ को मिलाइये।
सिद्ध करना है : $a r ({||}^{g m} A B C D) = a r ({||}^{g m} B P R Q)$
उपपत्ति : चूँकि AC तथा PQ क्रमशः चतुर्भुजों ABCD तथा BPRQ के विकर्ण हैं।
$∴ a r (Δ A B C) = \frac{1}{2} a r ({||}^{g m} A B C D)$ ...(i)
तथा $a r (Δ P B Q) = \frac{1}{2} a r ({||}^{g m} B P R Q)$ ...(ii)
अब $Δ A C Q$ तथा $Δ A Q P$ एक ही आधार AQ तथा समान समांतर रेखाओं AQ तथा CP के बीच स्थित हैं।
$∴ a r (Δ A C Q) = a r (Δ A Q P)$
$\Rightarrow a r (Δ A C Q) = a r (Δ A B Q) = a r (Δ A Q P) - a r (Δ A B Q)$ [ दोनों पक्षों में से $a r (Δ A B Q)$ घटाने पर ]
$\Rightarrow a r (Δ A B C) = a r (Δ B P Q)$
$\Rightarrow \frac{1}{2} a r ({||}^{g m} A B C D) = \frac{1}{2} a r ({||}^{g m} B P R Q)$ [(i) तथा (ii) का प्रयोग करने पर]
$\Rightarrow a r ({||}^{g m} A B C D) = a r ({||}^{g m} B P R Q)$

|

Updated on:21/07/2023

Class 9 MATHS AREA OF PARALLELOGRAMS AND TRIANGLES

Topper's Solved these Questions

Similar Questions

RD SHARMA-समांतर चतुर्भुजों और त्रिभुजों के क्षेत्रफल -बहु विकल्पीय प्रश्न

Home
Ask Doubt
Profile