A constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?

a. The direction of the frictional force will be in backwark direction of motion of the wheel.
10−f=ma
Substituting m=10kg and a=0.60m/s2 in the above equation, we get
Fr=4N
b. Equation of motion for rotation of wheel
fr×R=Iα
which gives
I=fr×Rα4×0.30(0.600.30)
or I=0.6kgm2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A sphere rolling on a horizontal rough surface Collides elastically with a smooth vertical wall, as shown in Fig. State which of the following statements is true or false.
 a. After collision, the velocity of the centre of mass gets reversed.
a. After collision, the velocity of the centre of mass gets reversed.
b. Angular momentum of the sphere about the point of contact with the wall is conserved.
c. Angular momentum of the sphere about a stationary point on the horizontal surface is conserved.
d. Just after collision the point of contact with the horizontal surface is moving towards the wall.
e. After collision the friction force acts on the sphere such that it decreases the linear speed and increases the angular speed.
f. Finally, when the sphere starts rolling, it is moving away from the wall.
View SolutionA uniform thin circular ring of mass m(m=0.4kg) and radius R has a small particle of the same mass m fixed on it as shown in Fig. The line joining the particle to centre is initially horizontal. The ground is frictionless. Find the contact force (magnitude) exerted by the ground on the ring, when the system is released from rest.

View SolutionA circular disc of mass M1 and radius R, initially moving, With a constant angular speed ω is gently placed coaxially on a stationary circular disc of mass M2 and radius R, as shown in Fig. There is a frictional force between the two discs.
If disc M2 is placed on a smooth surface, then 'determine' the final angular speed of each disc.
b. Determine the work done by friction.
c. Determine the frictional loss in kinetic energy. i.e. △K/Ki
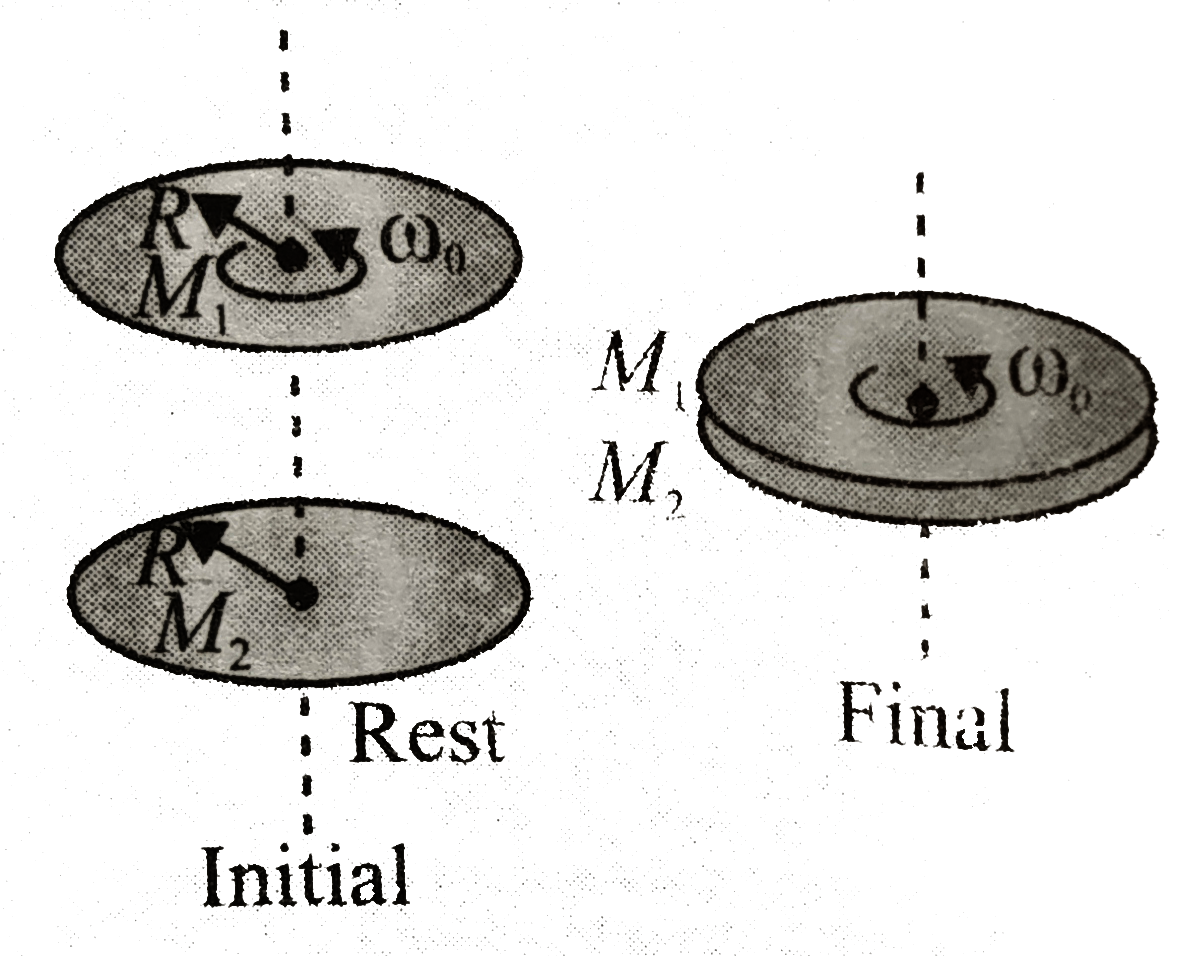
View SolutionA solid cylinder with r=0.1m and mass M=2kg is placed such that it is in contact with the vertical and a horizontal surface as shown in Fig. The coefficient of friction is μ=(1/3) for both the surfaces. Find the distance (in CM) from the centre of the cylinder at .which a force F=40N should be applied vertically so that the cylinder just starts rotating in anticlockwise direction.

View SolutionThe average power transmitted across a cross section by two sound waves moving in the same direction are equal. The wavelength of two sound waves are in the ratio of 1:2, then find the ratio of their pressure amplitudes.
View SolutionA wheel is rolling without slipping on a horizontal plane with velocity v and acceleration a of centre of mass as shown in figure. Acceleration at
View SolutionCalculate the force F that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height 0.4 m . Radius of wheel is 1m and mass = 10 kg . F is
View SolutionA wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
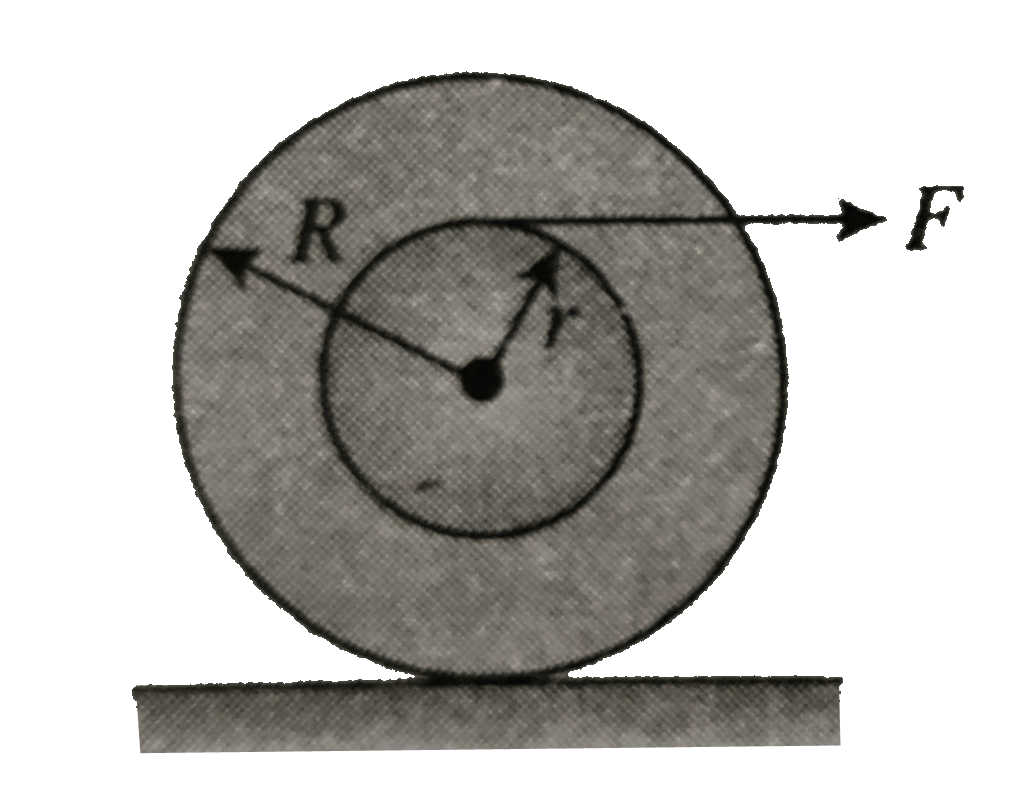
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
View SolutionA solid cylinder wheel of mass M and radius R is pulled by a force F applied to the centre of the wheel at 37^@ to the horizontal. If the wheel is to roll without slipping, what is the maximum value of |F| ? The coefficients of static and kinetic friction are mu_(s)=0.40 and m_(k)=0.30. (sin37^@=3/5)
View SolutionA wheel is rolling without slipping on a horizontal surface. In an inertial frame of reference in which the surface is at rest, is the reanypoint on the wheel that has a velocity that is purely vertical ? Is there any point that has a horizontal velocity component opposite to the velocity of the centre of mass ? Explain. What would be the results if wheel is slipping with rolling ?
View Solutionएक गाड़ी किसी सड़क पर 8 मीटर/(सेकण्ड)2 के त्वरण से गतिमान है। गाड़ी के पहिये की त्रिज्या 50 सेमी तथा जड़त्व आघूर्ण 10 किग्रा-(मीटर)2 है। यदि पहिया बिना फिसले लुढक रहा है तो पहिये पर कार्यरत् घर्षण बल कितना है?
यदि पहिये का द्रव्यमान 40 किग्रा हो तो सड़क व पहिये के बीच घर्षण गुणांक क्या है? (g = 10 मीटर/(सेकण्ड))
View Solution1 किग्रा द्रव्यमान तथा 50 सेमी त्रिज्या का एक वलयाकार पहिया तल पर 4 मीटर/सेकण्ड के वेग से बिना फिसले लुढ़क रहा है। पहिये का कोणीय संवेग ज्ञात कीजिये
View Solutionएक पहिया संलग्न चित्र के अनुसार किसी क्षैतिज तल पर 10 मीटर/सेकण्ड के वेग से बिना फिसले लुढ़कते हुए गतिमान है। पहिये के उच्चतम बिन्दु T, का रेखीय वेग क्या है?

View SolutionA wheel of mass 5 kg and radius 0.4 m is rolling on a road without sliding with angular velocity 10 rad.s−1. The moment of inertia of the wheel about the axis of rotation is 0.65 kg . m2. What is the percentage of the kinetic energy of rotation in the total kinetic energy of the wheel ?
View SolutionA wheel rolls smoothly along a floor while being accelerating horizontally by a force →Fn applied at its top. The wheel has radius R = 0.500 m, mass m = 1.60 kg, and acceleration magnitude a=2.00m/s2. The frictional force on the wheel is in the forward direction and has magnitude f = 1.80 N. What is the rotational inertia of the wheel?
View Solution

