Find the acceleration of the body if a force F=8N pulls the string at P that passes over the body and it is connected by another string to a rigid support at Q.
(Take radius of gyration k=2√3m,R=2m,r=1m, and mass of the body m=3kg)

a=αR
F−T=ma
Torque about C

TR−Fr=Iα
⇒TR−Fr=mk2aR
Pure the value of T from eqn i
(F−ma)R−Fr=mk2aR
F(R−r)=a[mk2R+mR]⇒a=FR(R−r)(k2+R2)m
=8×2×(2−1)(43+4)×3=8×2×14×43×3=1m/s2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
Find the acceleration (in m/s2) produced in a body of mass 2 kg when a force of 8 N is applied on it.
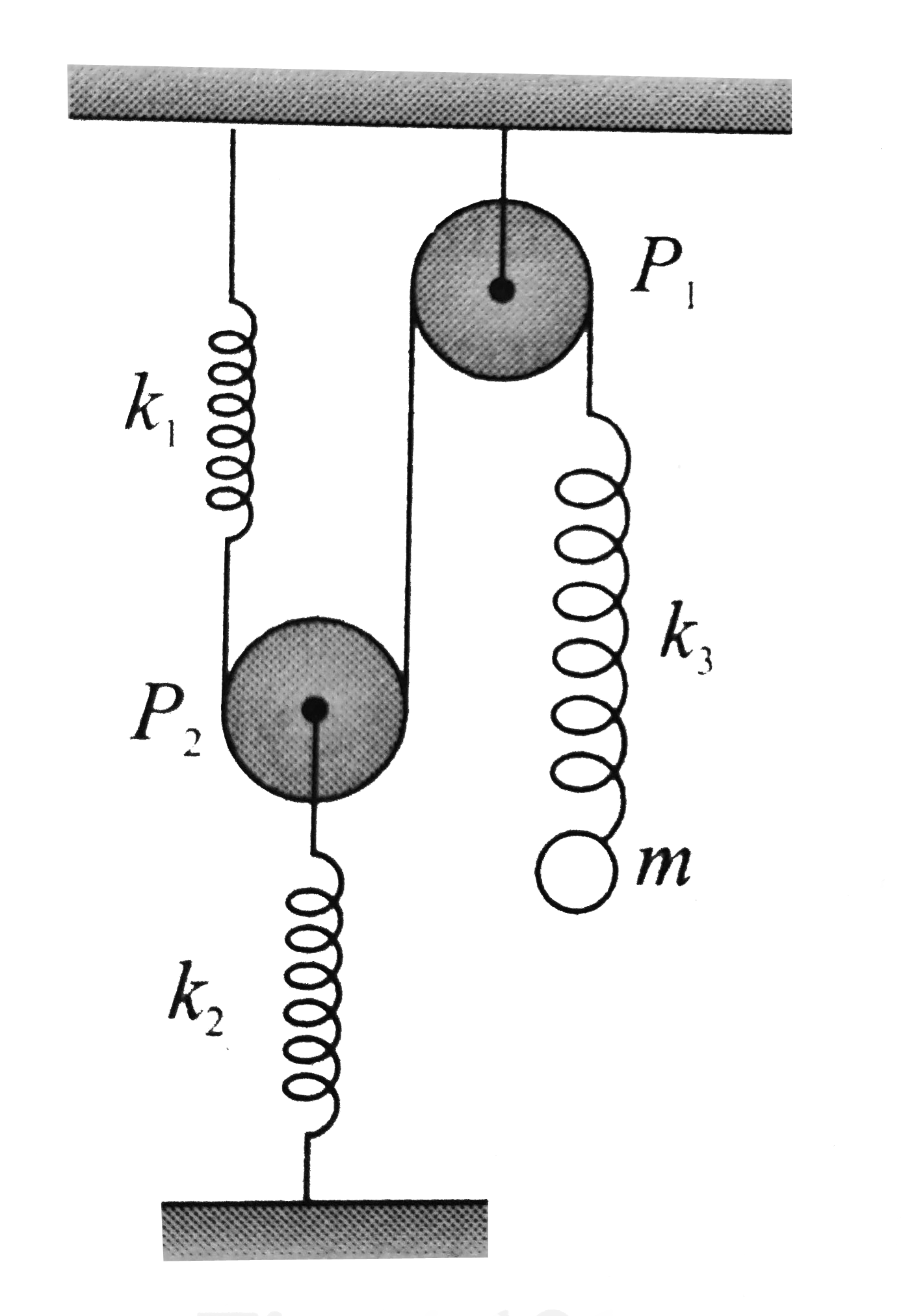
View SolutionA body of mass m hangs from a smooth fixed pulley P1 by the inextensible string fitted with the springs of stiffness k1 and k2 . The string passes over the smooth light pulley P2 which is connected with another ideal spring of stiffness k2. Find the period of oscillation of the body.
View Solution
Knowledge Check
Find the acceleration of the body if a force F=8N pulls the string at P that passes over the body and it is connected by another string to a rigid support at Q. (Take radius of gyration k=2√3m,R=2m,r=1m, and mass of the body m=3kg).
 .A1m/s2B1.5m/s2C1.2m/s2D2m/s2
.A1m/s2B1.5m/s2C1.2m/s2D2m/s2A body of mass M is being pulled by a string of mass m with a force P applied at one end. The force exerted by the string on the body is
APm(M+m)BPM(M+m)CPm(M+m)DP(M−m)Find the acceleration (in m/s2 ) produced in a body of mass 3 kg when a force of 6N is applied on it.
A18B4C2D36
Find the acceleration (inm/s2) produced in a body of mass 10 kg when a force of 20 N is applied on it.
View SolutionIf R is the radius of gyration of a body of mass M and radius r, then the ratio of its rotational to translational kinetic energy in the rolling condition is
View SolutionA torque of 2 newton-m produces an angular acceleration of 2rad/sec2 a body. If its radius of gyration is 2m, its mass will be:
View SolutionA body of mass 1 kg is suspended from a string 1 m long it is rotated in a vertical circle , what is the tension in the string when it is horizontal and the speed of the body is 2m/s ?
View SolutionA force F=(3ˆi+2ˆj+6ˆk)N produces acceleration of 1m/s2 in a body. The mass of the body is
View Solution

