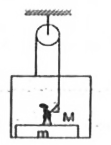
A cylinder of mass at and radius R rolls on a stationary plank of mass M. The lower surface of the plank is smooth and the upper surface is sufficiently rough with a coefficient of friction μ. A man is to hold the plank stationary with respect to the ground, as shown Fig.
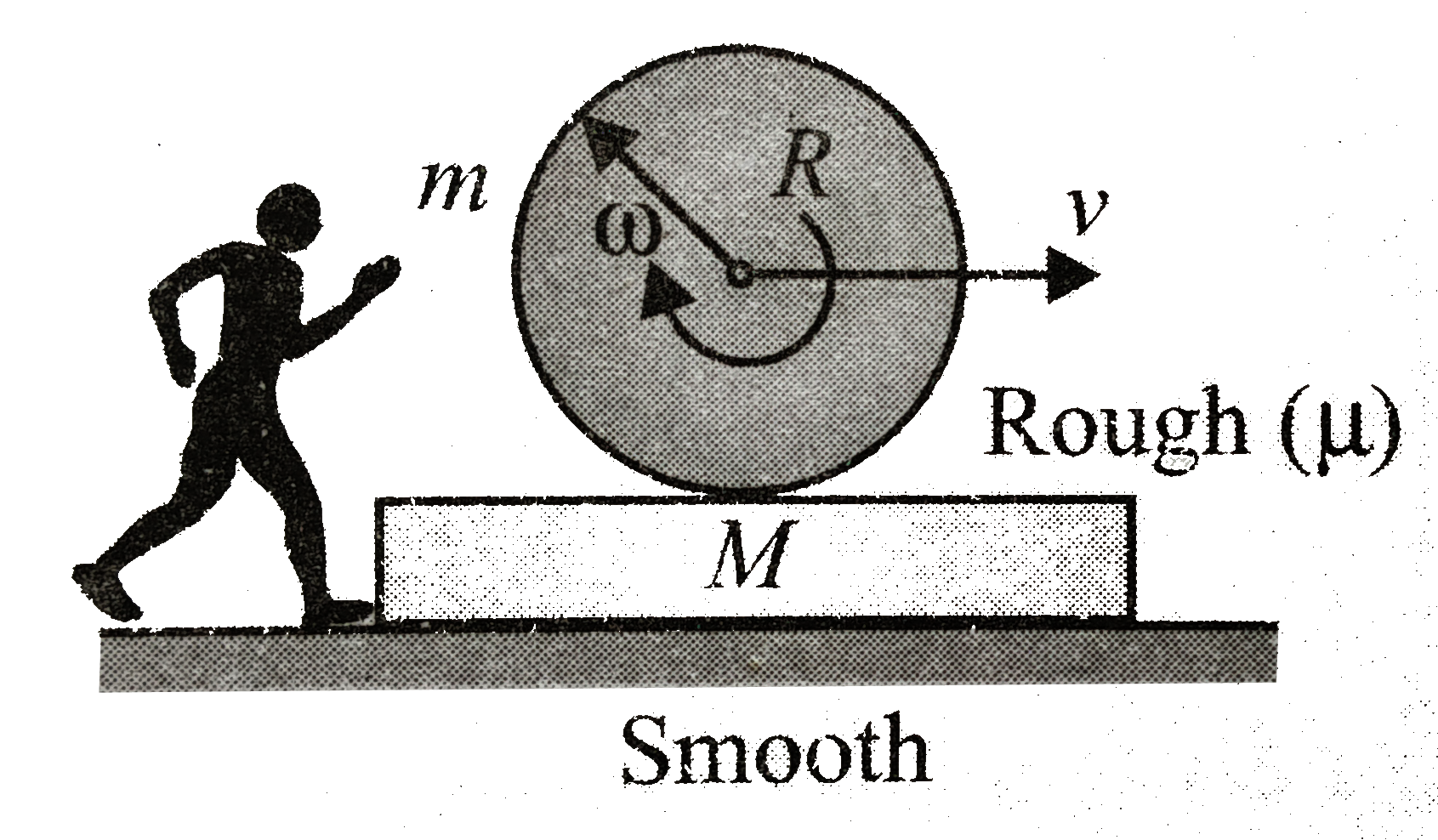
The force exerted by the man to keep the plank stationary is equal to……
Zero. Since lowest point of the sphere is stationary wit respect to the plank, therefore friction force acting on te plank is zero. Thus, no force is required to keep the plank statiorary.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA cylinder of mass M = 2 kg and radius R = 12 cm lies on a plank of the same mass as shown in the figure. The surface between plank and ground is smooth but there is friction between cylinder and plank. If the coefficient of friction between the cylinder and the plank is μ=0.4, then what maximum initial compression (in cm) can be given to the spring such that the cylinder moves without slipping with respect to the plank ? [Given, k=200 N m−1]
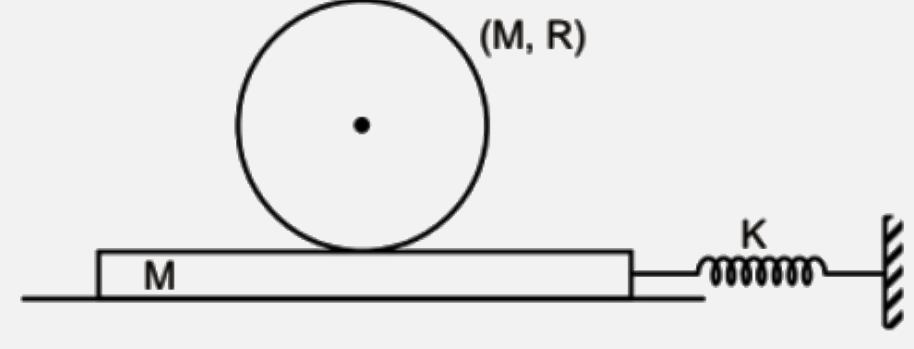
View Solution
Knowledge Check
A cylinder of mass M and radius R lies on a plank of mass M as shown. The surface between plank and ground is smooth, and between cylinder and plank is rough. Assuming no slipping between cylinder and plank, the time period of oscillation (When displaced from equilibrium) of the system is
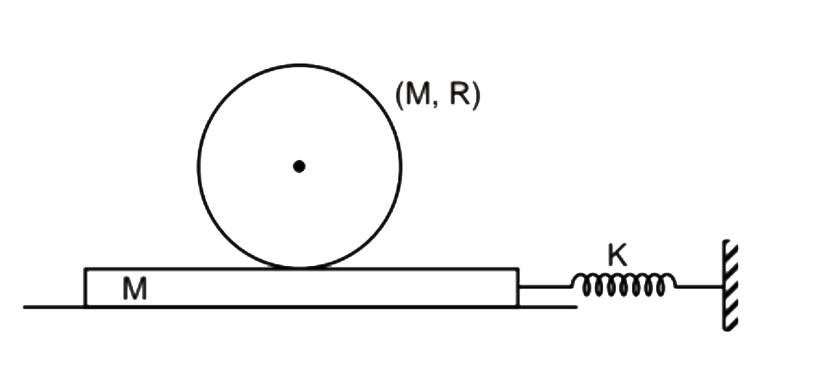 A2π√m3kB4π√2m3kC4π√M3kD4π√3M2k
A2π√m3kB4π√2m3kC4π√M3kD4π√3M2kA disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Force of friction between the disc and the plank isAF2BF4CF3D2F3A disc of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between disc and plank to prevent slipping. A force F is applied at the centre of the disc.

Acceleration of the plank isAF2mB3F4mCF4mD3F2m
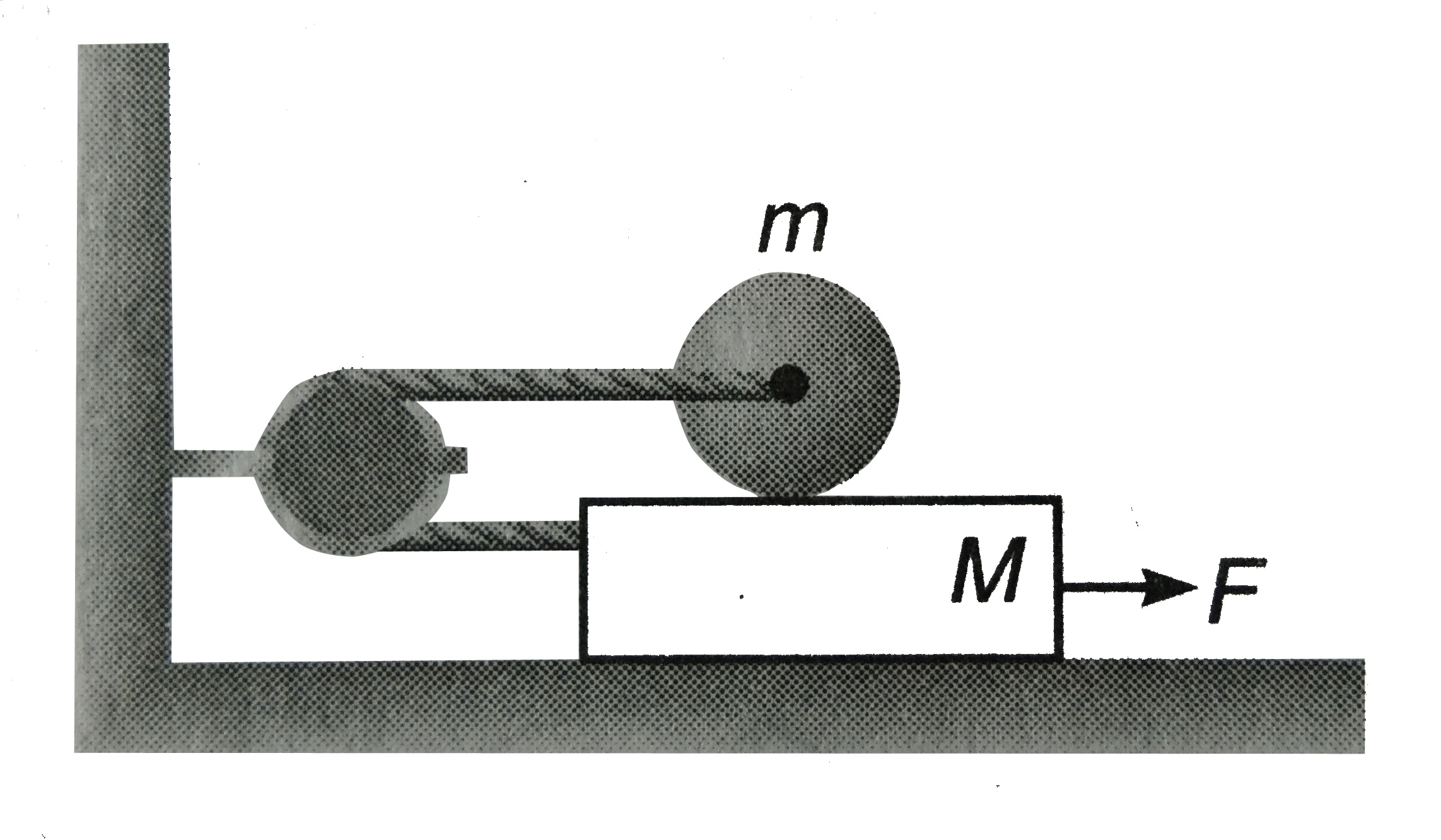
Find the acceleration of the cylinder of mass m and radius R and that of plank of mass M placed on smooth surface if pulled with a force F as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.
View SolutionIn the figure shown, a solid sphere of mass 'm' and radius r is released from a height 6r to slide down a smooth surface. A plank of same mass 'm' touches the horizontal portion of the surface at the ground. The co-efficient of friction between the plank and the sphere is μ and that between the plank and the ground is μ/4. Find the work done by the friction force between the plank and the ground till the sphere starts pure rolling on the plank. Neglect the height of the plank.

View SolutionA man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
View SolutionConsider a disc of mass m and radius R placed on a rough plank of mass M which is turn is place on a smooth horizontal surface. Now plank is pulled by a force F and disc starts to roll on the plank.
If there is no friction any where then find
(a) Fricition force acting on the disc
(b) Angular acceleration of the disc

View SolutionA cylinder is rolling without slipping on a horizontal plane P. The friction between the plank P and the cylinder is sufficient for no slipping. The coefficient of friction between the plank and the ground surface is zero. Initially, P is attached with a string S as shown in the figure. If the string is now burned, then.
View Solution
