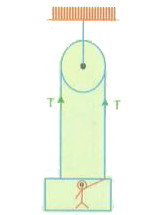
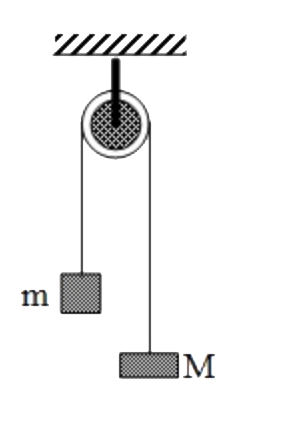
A man of mass M is standing on a plank kept in a box. The plank and box as a whole has mass m. A light string passing over a fixed smooth pulley connects the man and box. If the box remains stationary, find the tension in the string and the force exerted by the man on the plank.
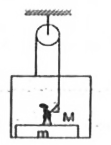
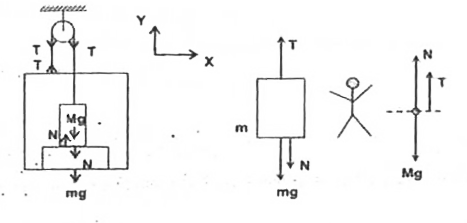
The fixed pulley is taken as frame of reference. The forces on man and box with plank are shown in figure.
The forces are as follows:
i. Weight of the man = Mg
ii. The tension in the string = T.
iii. The normal contact force between the man and the plank = N.
iv. The weight of the plank and box = mg
Referring to figure. The equation of motion of the man is given as
T+N−Mg=Ma
since M>m and the box remains at rest, the man will have to be at rest
T+N−Mg=0 ...(1)
Similarly referring to figure,
T−N−mg=ma=0 ...(2)
Solving (1) and (2) we obtain,
T=(M+m)g2andN=(M−m)g2
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - SOLVED PROBLEMS (SUBJECTIVE)
11 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - SOLVED PROBLEMS (OBJECTIVE)
17 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS DECIMAL TYPE
5 Videos
- MAGNETICBOOK - FIITJEECHAPTER - MAGNETICEXERCISE - Numerical Based Type
2 Videos
Similar Questions
A small block of mass m is placed on a plank of masss M .The block is connected to plank with the help of a light string passing over a light smooth pulley shown in fig. The co-efficient of static friction between the plank is μ The co-efficient of friction between the plank and the horizontal force F applied on the block of mass m can make block not to slide relatively?

View SolutionFigure shows a light platform on which a man of mass M is standing and holding a string passing over a system of ideal pulleys. Another mass m is hanging as shown in fig. Find the force the man has to exert to maintain the equlibrium of system, and find the force exerted by the platform on the man. Also find the ratio of M/m.
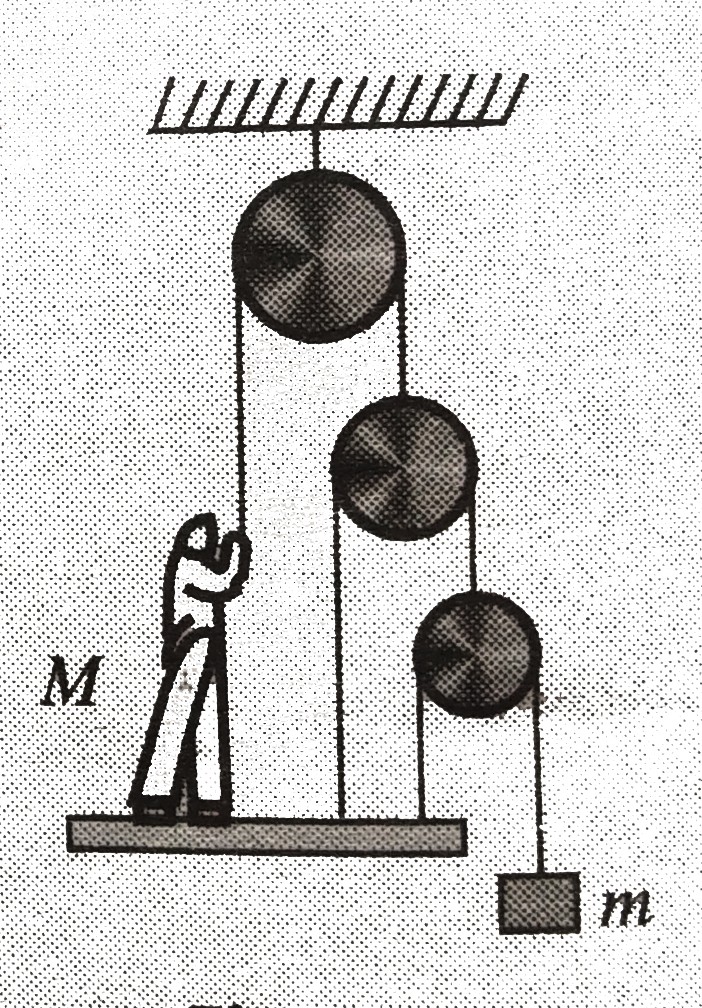
View Solution
Knowledge Check
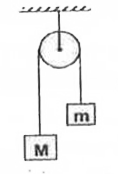
Two masses M and m(M>m) are joined by a light string passing over a smooth light pulley.
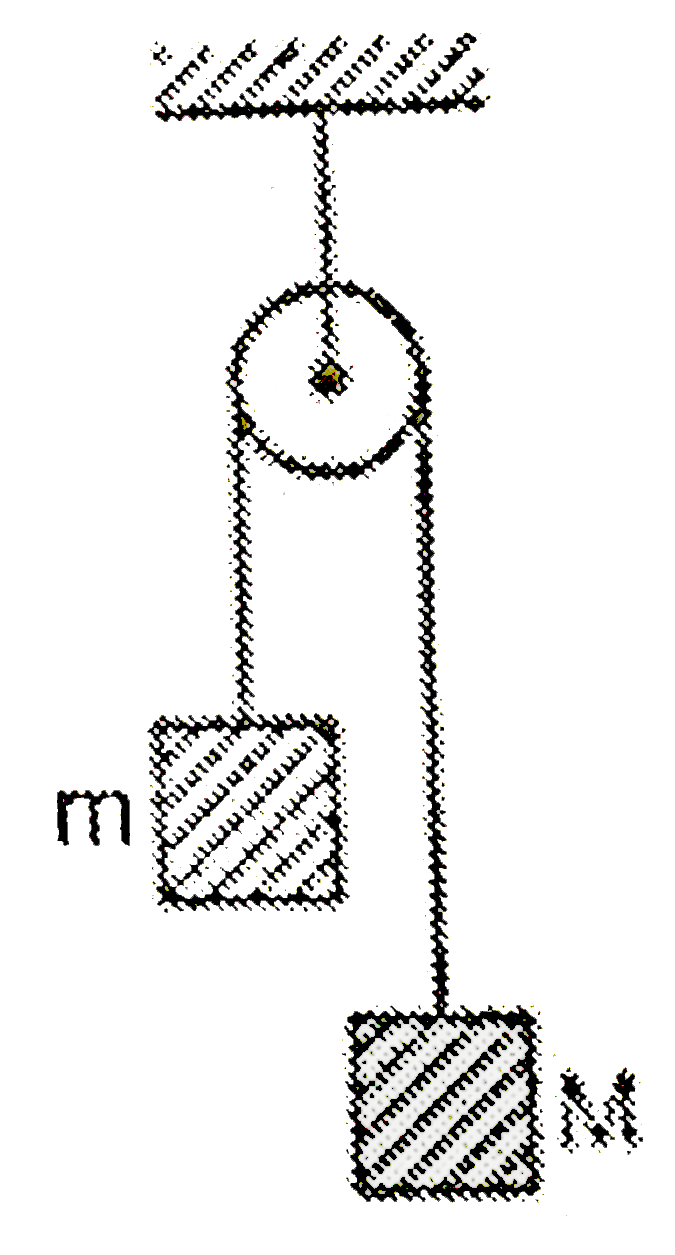 AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)g
AThe acceleration of each block is (M−mM+m)gBThe tension in the string is 2MmgM+mCThe centre of mass of the 'M plus m' system moves down with an acceleration of g(M−mM+m)2DThe tension in the string by which the pulley is attached to the rodd is (M+m)gTwo masses m and M(m<M) are joined by a light string passing over a smooth and light pulley (as shown)
 Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the above
Athe acceleration of each mass is (M−mM+m)gBthe tension in the string connecting masses is (2MmM+m)gCthe thrust acting on the pulley is (4MmM+m)gDNone of the aboveTwo masses ,each equal to m ,are arrached to one another by a massless string passing over a smooth pulley the tension in the string is :
AmgB2mgCmg/2Dzero
A small block of mass 'm' is placed on a plank of mass 'M'. The block is connected to plank with the help of a light string passing over a light smooth pulley as shown in figure. The co-efficient of static friction between the block and plank is μ.
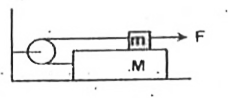
The co-efficient of friction between the plank and the horizontal surface is zero. What maximum horizontal force F applied on the block of mass m can make the block and plank not to slide relatively?
View SolutionTwo masses M and m are connected at the two ends of an inextensible string. The string passes over a smooth frictionless pulley. Calculate the acceleration of the masses and the tension in the string. Given M>m.
View SolutionA man of mass 60kg is standing on a weighing machine kept in a box of mass 30kg as shown in the diagram If the man man ages to keep the box stationary, find the read ing of the weighing machine
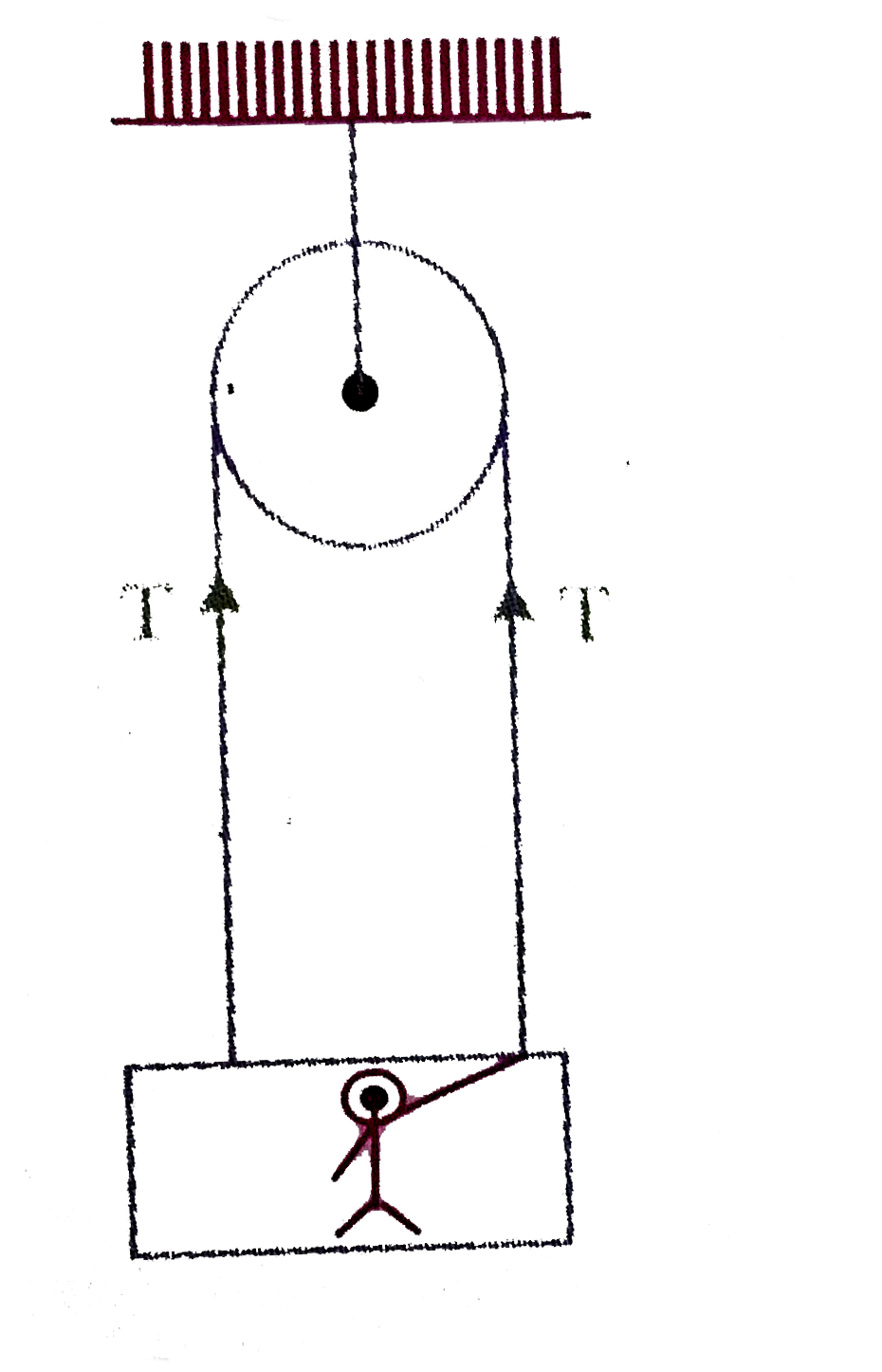 .
.
View SolutionA man of mass 60 kg is standing on a weighing machine kept in a box of mass 30 kg as shown in the diagram. If the man manages to keep the box stationary, find the reading of the weighing machine.
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
View Solution
