Two highways are perpendicular to each other : imagine them to be along the x-axis and the y-axis, respectively. At the instant t=0, a police car P is at a distance d= 400m from the intersection and moving at speed of 80km/h towards it along the x-axis. Motorist M is at a distance of 600m from the intersection and moving towards it at a speed of 60km/h along the y-axis . The minimum distance between the cars is
The correct Answer is:00240.00
To solve the problem of finding the minimum distance between the police car P and the motorist M, we can follow these steps:
Step 1: Define the initial positions and velocities
- The police car P is initially at a distance of dP=400m=0.4km from the intersection, moving towards it along the x-axis at a speed of vP=80km/h.
- The motorist M is initially at a distance of dM=600m=0.6km from the intersection, moving towards it along the y-axis at a speed of vM=60km/h.
Step 2: Write the equations for the positions of the cars over time
At time t (in hours):
- The position of the police car P along the x-axis is given by:
xP(t)=0.4−80t
- The position of the motorist M along the y-axis is given by:
yM(t)=0.6−60t
Step 3: Write the expression for the distance between the two cars
The distance D(t) between the two cars at time t can be expressed using the Pythagorean theorem:
D(t)=√(xP(t))2+(yM(t))2
Substituting the expressions for xP(t) and yM(t):
D(t)=√(0.4−80t)2+(0.6−60t)2
Step 4: Simplify the expression for distance
Squaring the distance to simplify calculations:
D2(t)=(0.4−80t)2+(0.6−60t)2
Expanding both squares:
D2(t)=(0.16−64t+6400t2)+(0.36−72t+3600t2)
Combining like terms:
D2(t)=0.52−136t+10000t2
Step 5: Minimize the distance
To find the minimum distance, we take the derivative of D2(t) with respect to t and set it to zero:
d(D2)dt=−136+20000t=0
Solving for t:
20000t=136⟹t=13620000=0.0068hours
Step 6: Calculate the minimum distance
Now we substitute t back into the expression for D(t):
D2(0.0068)=0.52−136(0.0068)+10000(0.0068)2
Calculating each term:
1. 0.52−136×0.0068=0.52−0.9248=−0.4048
2. 10000×(0.0068)2=10000×0.00004624=0.4624
Combining these:
D2(0.0068)=−0.4048+0.4624=0.0576
Thus, the minimum distance D is:
D=√0.0576≈0.24km=240m
Final Answer
The minimum distance between the police car and the motorist is 240 meters.
---
- The police car P is initially at a distance of dP=400m=0.4km from the intersection, moving towards it along the x-axis at a speed of vP=80km/h.
- The motorist M is initially at a distance of dM=600m=0.6km from the intersection, moving towards it along the y-axis at a speed of vM=60km/h.
At time t (in hours):
- The position of the police car P along the x-axis is given by:
xP(t)=0.4−80t
- The position of the motorist M along the y-axis is given by:
yM(t)=0.6−60t
The distance D(t) between the two cars at time t can be expressed using the Pythagorean theorem:
D(t)=√(xP(t))2+(yM(t))2
Substituting the expressions for xP(t) and yM(t):
D(t)=√(0.4−80t)2+(0.6−60t)2
Squaring the distance to simplify calculations:
D2(t)=(0.4−80t)2+(0.6−60t)2
Expanding both squares:
D2(t)=(0.16−64t+6400t2)+(0.36−72t+3600t2)
Combining like terms:
D2(t)=0.52−136t+10000t2
To find the minimum distance, we take the derivative of D2(t) with respect to t and set it to zero:
d(D2)dt=−136+20000t=0
Solving for t:
20000t=136⟹t=13620000=0.0068hours
Now we substitute t back into the expression for D(t):
D2(0.0068)=0.52−136(0.0068)+10000(0.0068)2
Calculating each term:
1. 0.52−136×0.0068=0.52−0.9248=−0.4048
2. 10000×(0.0068)2=10000×0.00004624=0.4624
D2(0.0068)=−0.4048+0.4624=0.0576
Thus, the minimum distance D is:
D=√0.0576≈0.24km=240m
The minimum distance between the police car and the motorist is 240 meters.
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS WITH SINGLE DIGIT
5 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Two highways intersect as shown in Fig. 4-39. At the instant shown, a police car P is distance dp=800m from the intersection and moving at speed vp=80km/h. Motorist M is
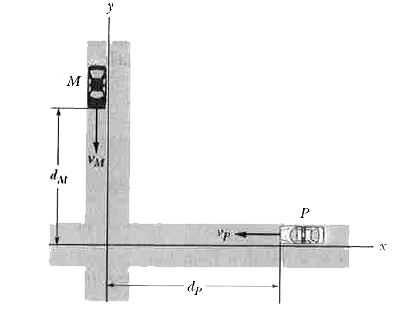
distance dM=600m from the intersection and moving at speed vM=60km/h. (a) In unit-vector notation, what is the velocity of the motorist with respect to the police car? (b) For the instant shown in Fig. 4-39, what is the angle between the velocity found in (a) and the line of sight between the two cars? (c ) If the cars maintain their velocities, do the answers to (a) and (b) change as the cars move nearer the intersection?
View SolutionA body starts from rest from the origin with an acceleration of 6m/s2 along the x-axis and 8m/s2 along the y-axis. Its distance from the origin after 4 seconds will be
View Solution
Knowledge Check
Two highways are perpendicular to each other imagine them to be along the x-axis and the y-axis, respectively. At the instant t=0, a police car P is at a distance d=400m from the intersection and moving at speed of 8km/h towards it at a speed of 60km/h along they y-axis. The minimum distance between the cars is
A300mB240mC180mD120mA car moving with a speed of 40km/h can be stopped by applying the brakes after at least 2 m. If the same car is moving with a speed of 80km/h, what is the minimum stopping distance?
A8mB2mC4mD6mA car moving with a speed of 40 km/h can be stopped by applying brakes after at least 2m. If the same car is moving with a speed of 80 km/h., what is the minimum stopping distance ?
A2 mB4 mC6 mD8 m
A body starts from rest from the origin with an acceleration of 3m/s(2) along the x-axis and 4m/s2 along the y-axis. Its distance from the origin after 2s will be
View SolutionRam Shyam are walking on two perpendicular tracks with speed 3ms−1and4ms−1, respectively. At a certain moment (say t = 0s), Ram and Shyam are at 20 m and 40 m away from the intersection of tracks, respectively, and moving towards the intersection of the tracks.
Shortest distance between them subsequently is
View SolutionA particle moves along x-axis with speed 6m/s for the first half distance of a journey and the second half distance with a speed 3m/s. The average speed in the total journey is
View SolutionA particle A is at origin and particle B is at distance y=−d at t=0. They move with constant velocity v, A towards positive x-axis and B towards origin. The time at which distance between them is minimum and minimum distance will be
View SolutionA car is moving on a straight road covers one third of the distance with a speed of 20 km/h and the rest with a speed of 60 km/h. The average speed of the car is
View Solution
