A particle A is at origin and particle B is at distance y=−d at t=0. They move with constant velocity v, A towards positive x-axis and B towards origin. The time at which distance between them is minimum and minimum distance will be
d2v,d
dv,d√2
d2v,d√2
dv,d
The correct Answer is:C
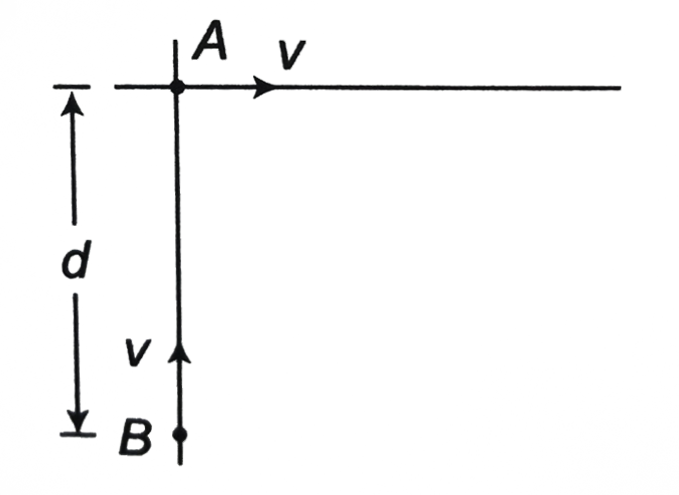
After time t,

s2=(vt)2+(d−vt)2
For s to be minimum,
dsdt or d(s2)dt=v2.2t+2(d−vt)(−v)=0
vt=(d−vt)⇒t=d2v
smin=√(d2)2+(d2)2=d√2
Topper's Solved these Questions
Similar Questions
Two cars A and B are running with same speed v. A along east and B towards north. Car A is at origin O and B is at distance d as shown. After how much time, the distance between cars is minimum and what is the minimum distance?
View Solution(i) A particle of mass m executes SHM in xy- plane along a straight line AB. The points A (a, a) and B (- a, - a) are the two extreme positions of the particle. The particle takes time T to move from one extreme A to the other extreme B. Find the x component of the force acting on the particle as a function of time if at t = 0 the particle is at A. (ii) Two particle A and B are performing SHM along X-axis and Y-axis respectively with equal amplitude and frequency of 2 cm and 1 Hz respectively. Equilibrium positions for the particles A and B are at the coordinate (3, 0) and (0, 4) respectively. At t = 0, B is at its equilibrium position and moving toward the origin, while A is nearest to the origin. Find the maximum and minimum distances between A and B during their course of motion
View Solution
Knowledge Check
Two particles move with constant velocities towards point O along straight lines in a plane as shown. The shortest distance A and B is
 A50√3cmB300cmC100√3cmD200cm
A50√3cmB300cmC100√3cmD200cmFor two particles vibrating in the same phase, the minimum distance between them is called
AWavelengthBFrequencyCAmplitudeDPhaseTwo particles are moving along x-axis. Particle-1 is 40m behind Particle-2. Particle-1 starts with velocity12m/s and acceleration 4m/s2 both in positive x-direction. Particle-2 starts with velocity 4m/s and acceleration 12m/s2 also in positive x-direction. Find
(a) the time when distance between them is minimum.
(b) the minimum distacne between them.A1s 36mB12s 36mC1s 360mD1s 136m
Two particles A and B performing SHM along x and y−axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the co-ordinates (3,0) and (0,4) respectively. At t=0,B is at its equilibrium positions and moving towards the origin, while A is nearest to the origin and moving away from the origin. If the maximum and minimum distances between A and B is s1 and s2 then find s1+s2 (in cm).
View SolutionA particle moves with constant acceleration a in the positive x-axis. At t=0 the particle is at origin is at rest , then correct graph between (velocity)2 and displacement is :
View SolutionParticles A and B are moving with constant velocities along x and y axis respectively, the graph of separation between them with time is
View SolutionTwo particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the coordinates [3cm,0] and (0,4cm) respectively. At t=0,B is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Minimum and maximum distance between A and B during the motion is-
View SolutionThe minimum stopping distance of a car moving with velocity u is x. If the car is moving with velocity 2v, then the minimum stopping distance will be.
View Solution
