A river is flowing from west to east with a speed of 5m/min. A man can swim in still water with a velocity 10m/min. In which direction should the man swim so as to take the shortest possible path to go to the south.
30∘ with downstream
60∘ with downstream
120∘ with downstream
South
The correct Answer is:C
To solve the problem of determining the direction in which a man should swim to take the shortest possible path to go south while a river flows from west to east, we can follow these steps:
1. Identify the velocities:
- The river flows from west to east with a velocity U=5m/min.
- The man can swim in still water with a velocity V=10m/min.
2. Understand the goal:
- The man wants to swim straight south. However, due to the river's current, he must swim at an angle upstream to counteract the eastward flow of the river.
3. Set up the vector diagram:
- Let the direction south be represented as the negative y-axis and the direction of the river (east) as the positive x-axis.
- The man's swimming direction will be at an angle θ from the south towards the west.
4. Use the Pythagorean theorem:
- The man's swimming velocity can be broken down into two components:
- The southward component: Vsin(θ)
- The westward component: Vcos(θ)
- To ensure he swims directly south, the westward component must equal the river's velocity:
Vcos(θ)=U
- Substituting the known values:
10cos(θ)=5
- Solving for cos(θ):
cos(θ)=510=12
5. Calculate the angle:
- Using the inverse cosine function:
θ=cos−1(12)=60∘
6. Determine the final direction:
- Since the angle θ is measured from the south towards the west, the man should swim at an angle of 60∘ from the south towards the west.
- To express this in terms of the downstream direction (east), we can say:
90∘+60∘=150∘
- Thus, the man should swim at an angle of 150∘ from the east (downstream).
Final Answer:
The man should swim at an angle of 60∘ from the south towards the west, or equivalently, 150∘ from the east (downstream).
- The river flows from west to east with a velocity U=5m/min.
- The man can swim in still water with a velocity V=10m/min.
- The man wants to swim straight south. However, due to the river's current, he must swim at an angle upstream to counteract the eastward flow of the river.
- Let the direction south be represented as the negative y-axis and the direction of the river (east) as the positive x-axis.
- The man's swimming direction will be at an angle θ from the south towards the west.
- The man's swimming velocity can be broken down into two components:
- The southward component: Vsin(θ)
- The westward component: Vcos(θ)
- To ensure he swims directly south, the westward component must equal the river's velocity:
Vcos(θ)=U
- Substituting the known values:
10cos(θ)=5
- Solving for cos(θ):
cos(θ)=510=12
- Using the inverse cosine function:
θ=cos−1(12)=60∘
- Since the angle θ is measured from the south towards the west, the man should swim at an angle of 60∘ from the south towards the west.
- To express this in terms of the downstream direction (east), we can say:
90∘+60∘=150∘
- Thus, the man should swim at an angle of 150∘ from the east (downstream).
The man should swim at an angle of 60∘ from the south towards the west, or equivalently, 150∘ from the east (downstream).
Topper's Solved these Questions
Similar Questions
A river is flowing from west to east with a speed 5 m s−1. A swimmer can swim in still water at a speed of 10 m s−1 .
If he wants to start from point A on south bank and reach opposite point B on north bank. In what direction direction should he swim ?
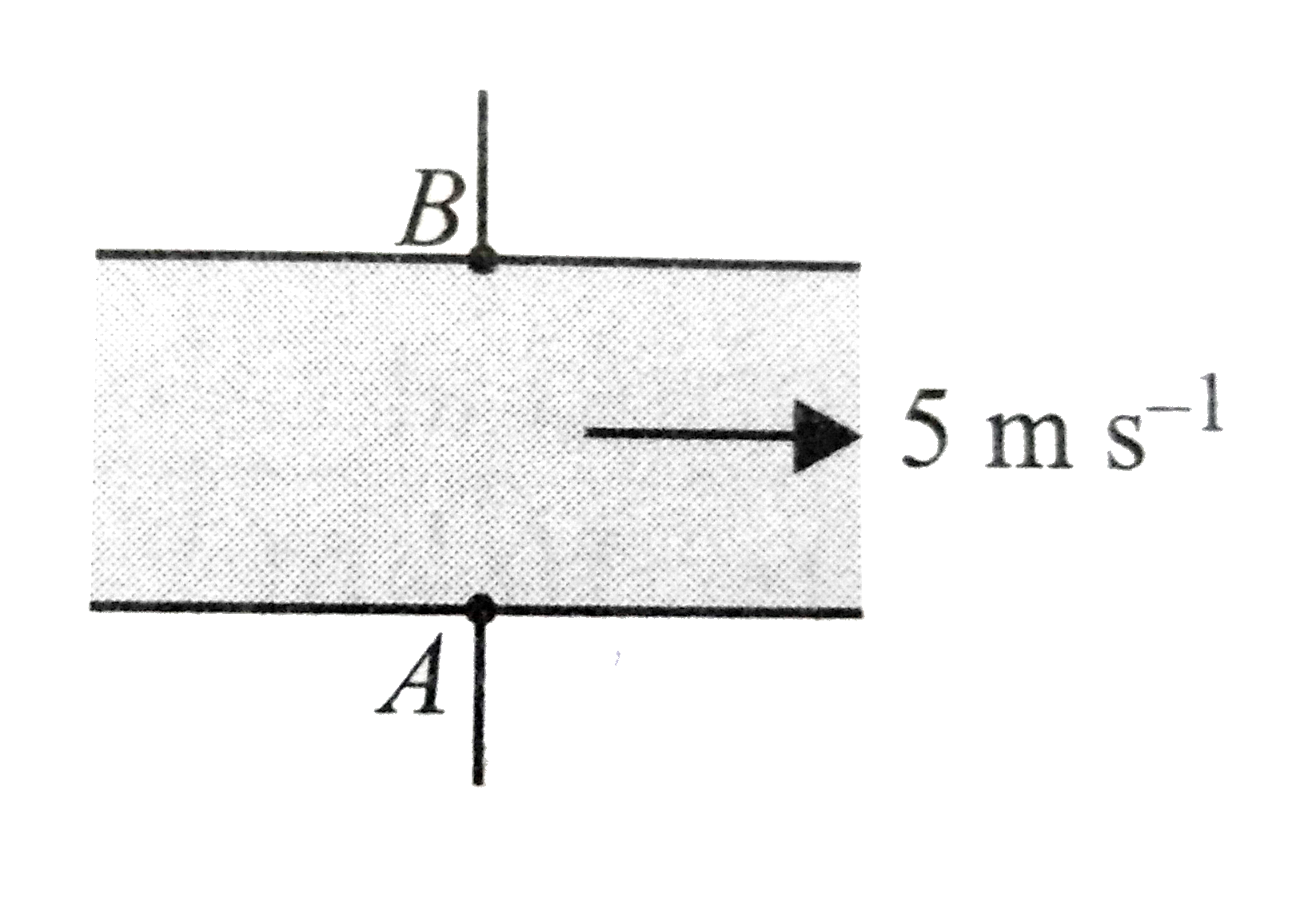
View SolutionA river is flowing from the west to the east at 5m/min. A swimmer on the southerm bank can swim at 10 m/min in still water. In what direction should he swim if (i) He wishes to cross the river in minimum time (ii) He wishes to cross te river through shortest route
View Solution
Knowledge Check
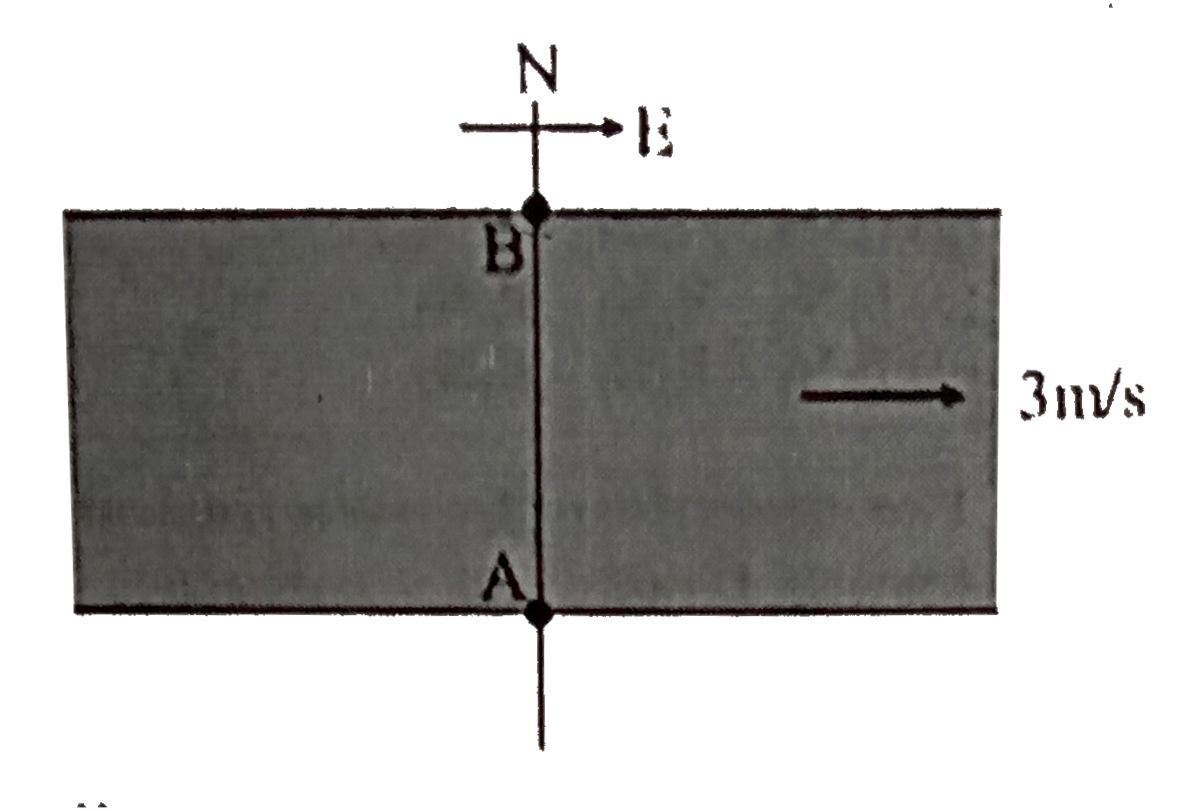
A river is flowing from east to west at a speed of 5m/min. A man on south bank of river, capable of swimming 10m/min in still water, wants to swim across the river in shortest time. He should swim
ADue northBDue north -eastCDue north-east with double the speed of riverDNone of theseA river is flowing from east to west at a speed of 5mmin. A man on south bank of river, capable of swimming 10mmin ini still water, wants to swim across the river in shortest time. He should swim
ADue northBdue north-eastCdue north-east with double the speed of riverDnone of theseA river is flowing from west to east at a speed of 5 metres per minute.A man on the south bank of the river, capable of swimming at 10 metres per minute in still water, wants to swim across the river in the shortest time. He should swim in a direction.
Adue northB30∘ east of northC30∘ west of northD60∘ east of north
Statement-1: A river is flowing from east to west at a speed of 5m/min. A man on south bank of river, capable of swimming 10 m/min in still water, wants to swim across the river in shortest time. He should swim due north. Statement-2 : For the shortest time the man needs to swim perpendicular to the bank.
View SolutionA man can swim at the rate of 5kmh−1 in still water. A 1−km wide river flows at the rate of 3kmh−1 The man wishes to swim across the river directly opposite to the starting point.
(a) Along what direction must the man swim ?
(b) What should be his resultant velocity ?
( c) How much time will he take to cross the river ?
View SolutionA river flowing from east to west at a speed of 5m/min. A man on south bank river, capable of swimming 10m/min in still water, wants to swim across the river in shorter time, he should swim:-
View SolutionA river is flowing from east to west at a speed of 5m/min. A man on south bank of river, capable of swimming 10m/min in still water, wants to swim across the river in shortest time. He should swim
View SolutionA river is flowing due east with a speed 3m/s. A wimmer can swim in still water at a speed of 4m/s. If swimmer starts swimming due north, what will be his resultant velocity (magnitude and direction) ?
View Solution

