A spool (consider it as a double disc system joined by a short tube at their centre) is placed on a horizontal surface as shown Fig. A light string wound several times over the short connecting tube leaves it tangentially and passes over a light pulley. A weight of mass m is attached to the end of the string. The radius of the connecting tube is r and mass of the spool is M and radius is R. Find the acceleration of the falling mass m. Neglect the mass of the connecting tube and slipping of the spool.

Since there is no slipping, the velocity of the point of contact of the string with the pulley is the vector sum of the velocity of the point of contact due to rotation plus the velocity of the centre of mass of the spool. That is
vB=vCM=ωr,ω is in clockwise direction.
But vCM=ωR
vB=vCM−vCMrR=vCM(R−rR)
This also the velocity v of the rolling mass
vB=vCM(R−rR)=v(R−rR)
Cosidering the conservation of energy when m lowers by h, we get mgh=12mv2+(12Mv2CM+12Iω2)
=12mv2+(12Mv2CM+12×12MR2v2CMR2)
=12mv2+34Mv2CM
=12mv2+34Mv2(RR−r)
v2=4mgh2m+3M[RR−r]2
Comparing with v2=2ah
a=v22h=2mg2m+3M[R/(R−r)]2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.2
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
View SolutionA light string passes over a frictionless pulley. To one of its ends a mass of 6 kg is attached. To its other end a mass of 10 kg is attached. The tension in the thread will be
View Solution
Knowledge Check
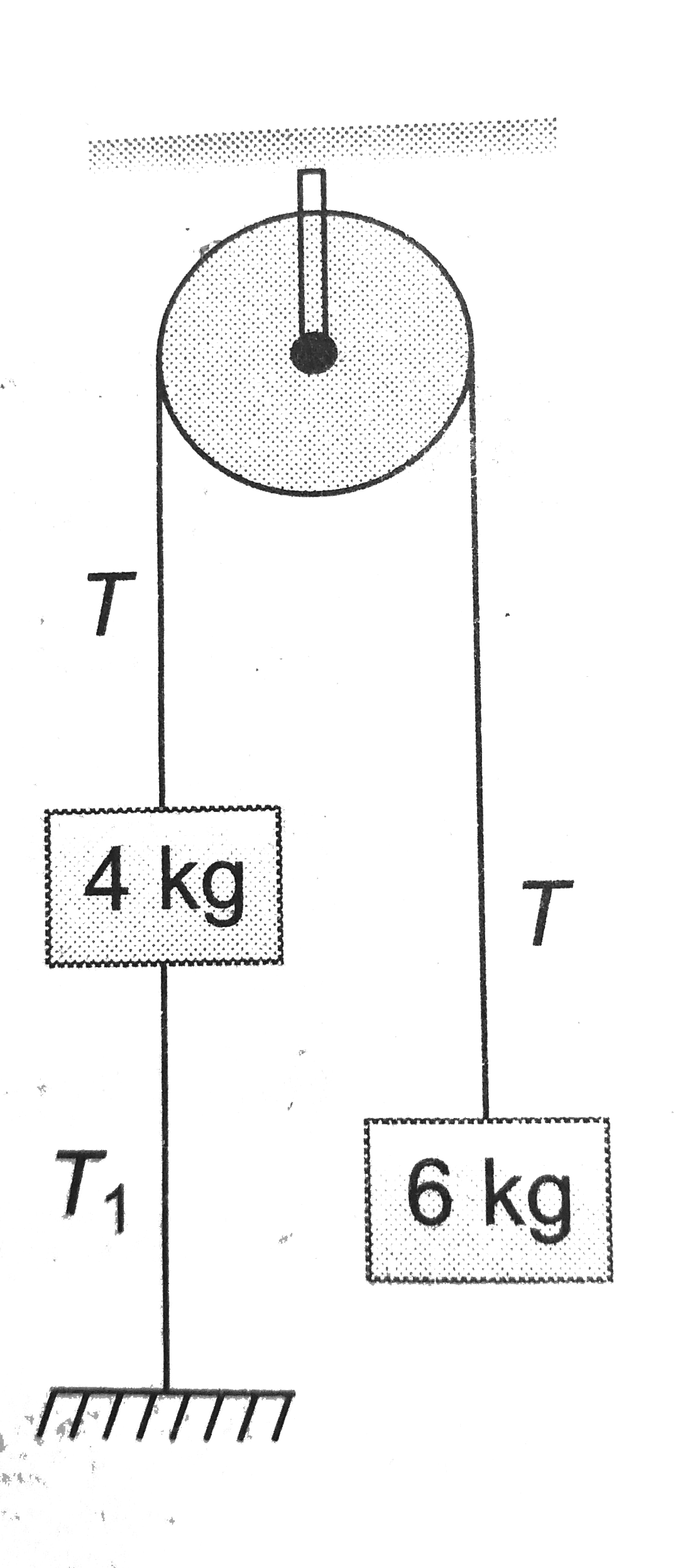
Two bodies of masses 4kg and 6kg are attached to the ends of a string which passes over a pulley, the 4kg mass is attached to the table top by another string.The tension in this string T1 is equal to
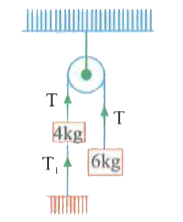 A10NB10.6NC25ND20N
A10NB10.6NC25ND20NA block of mass m is attached at the end of an inextensible string which is wound over a rough pulley of mass M and radius R. Assume the string does not slide over the pulley. Find the acceleration of the block when released.
Amg2m+MB2mgm+MCmgm+MD2mg2m+MA block of mass 2 m hangs by an inextensible light string that passes over a smooth pulley. Another mass m hangs from the other end of the string and is connected to a vertical massless spring. The system is stationary. Just after the string is cut, the accelerations of m and 2m, respectively, are -
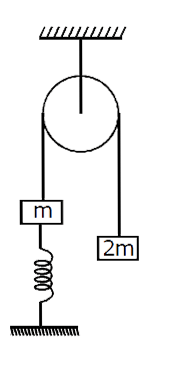 A0,0B0,g↓Cg2⏐⏐ ⏐↓g⏐⏐ ⏐↓D2g↓,g↓
A0,0B0,g↓Cg2⏐⏐ ⏐↓g⏐⏐ ⏐↓D2g↓,g↓
Two masses 2 kg and 3 kg are attached to the end of the string passed over a pulley fixed at the top. The tension and acceleration are
View SolutionTwo bodies of mass 4kg and 6kg are attached to the ends of a string passing over a pulley. The 4kg mass is attached to the table top by another string. The tension in this string T1 is equal to: Take
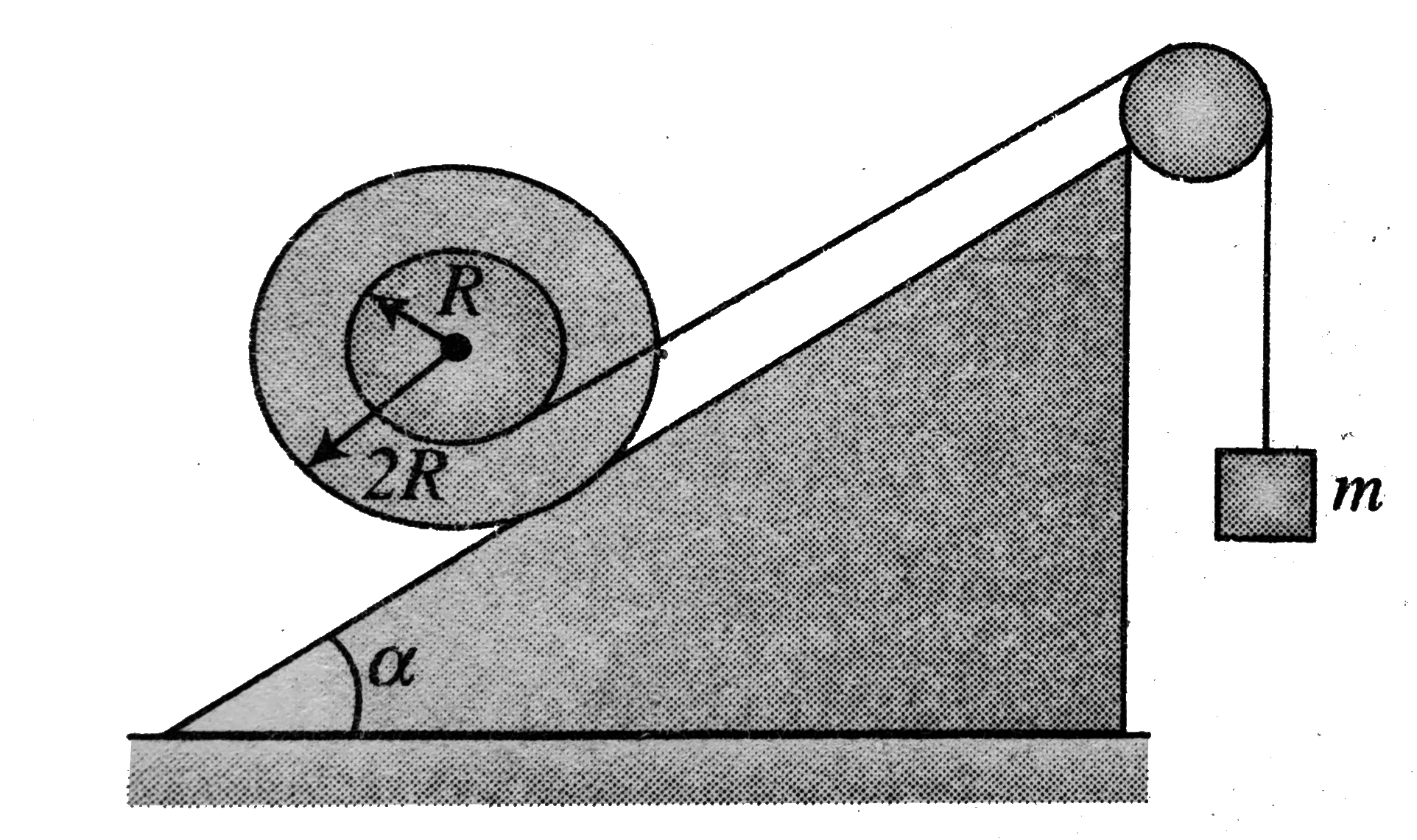
View SolutionA spool of mass M and radius 2R lies on an inclined plane as shown in the figure. A light thread is wound around the connecting tube of the spool and its free end carries a weight of mass m. The value of m so that system is in equilibrium is
View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
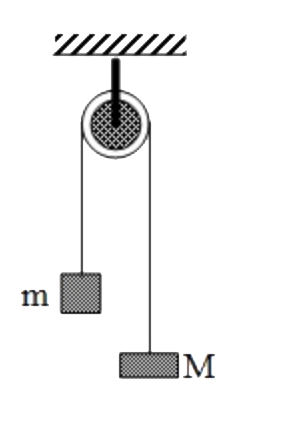
View SolutionTwo masses m and M(>m) are joined by a light string passing over a smooth light pulley. The centre of mass of the system moves with an acceleration
View Solution

