A solid sphere of mass $M$ is placed on the top of a plank of the same mass, after giving an angular velocity $ω_{0}$ at $t = 0$ . Find the velocity of the plank and the sphere when the sphere starts rolling:,

Video Solution

Text Solution

Verified by Experts

Step 1: Free body diagram

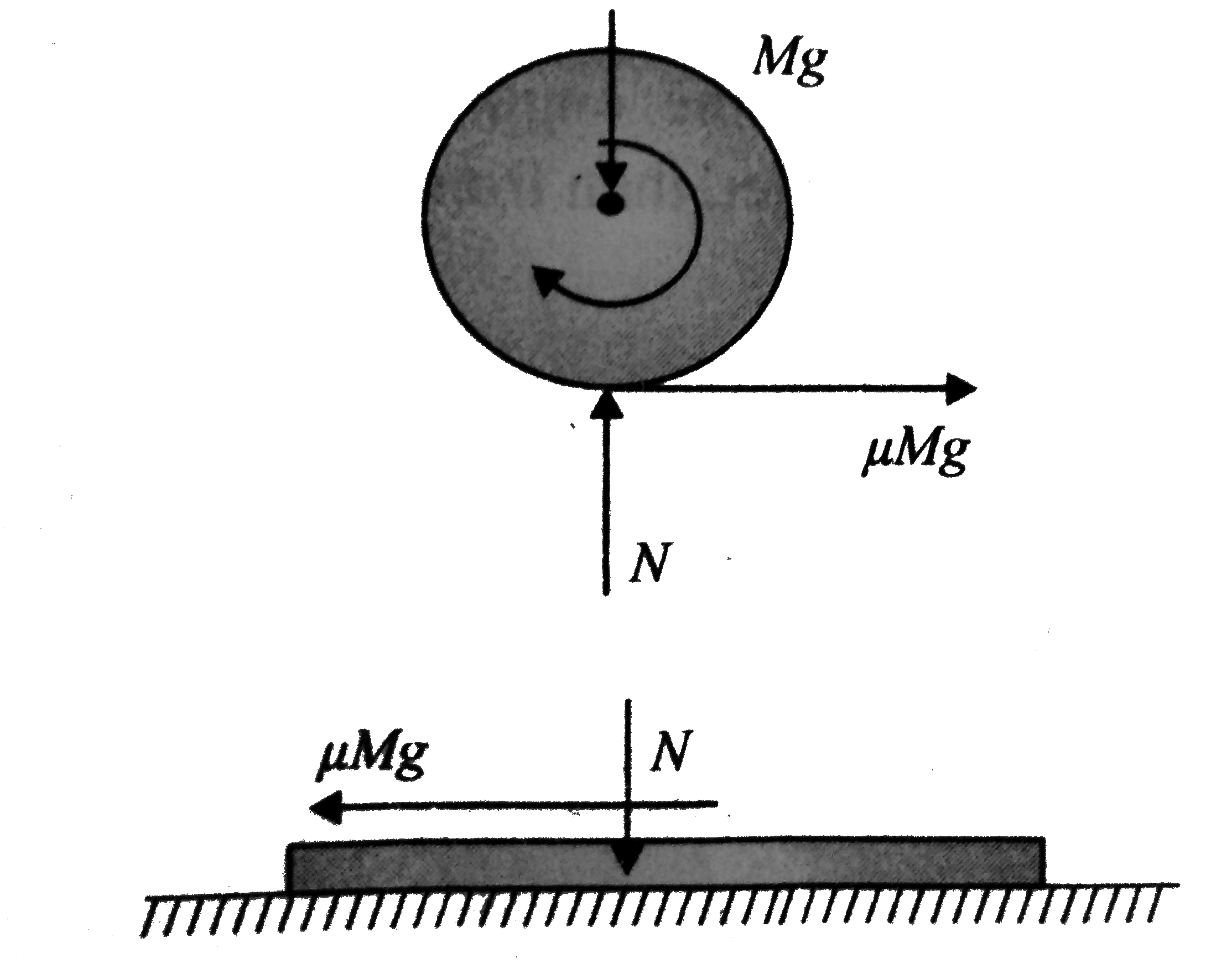
Step 2: Equation of motion,
$μ M g = M A \Rightarrow A = μ g$ (backward)
(A will be positive)
sphere
$μ M g = M A \Rightarrow a = μ g$ (forward)
(a will be positive)
Step: Torque equation
$μ M g R = (\frac{2}{5} M R^{2}) α$
$α = \frac{5}{2} \frac{μ g}{R}$ (anticlockwise)
(it will be negative )
Step 4: constraint relation

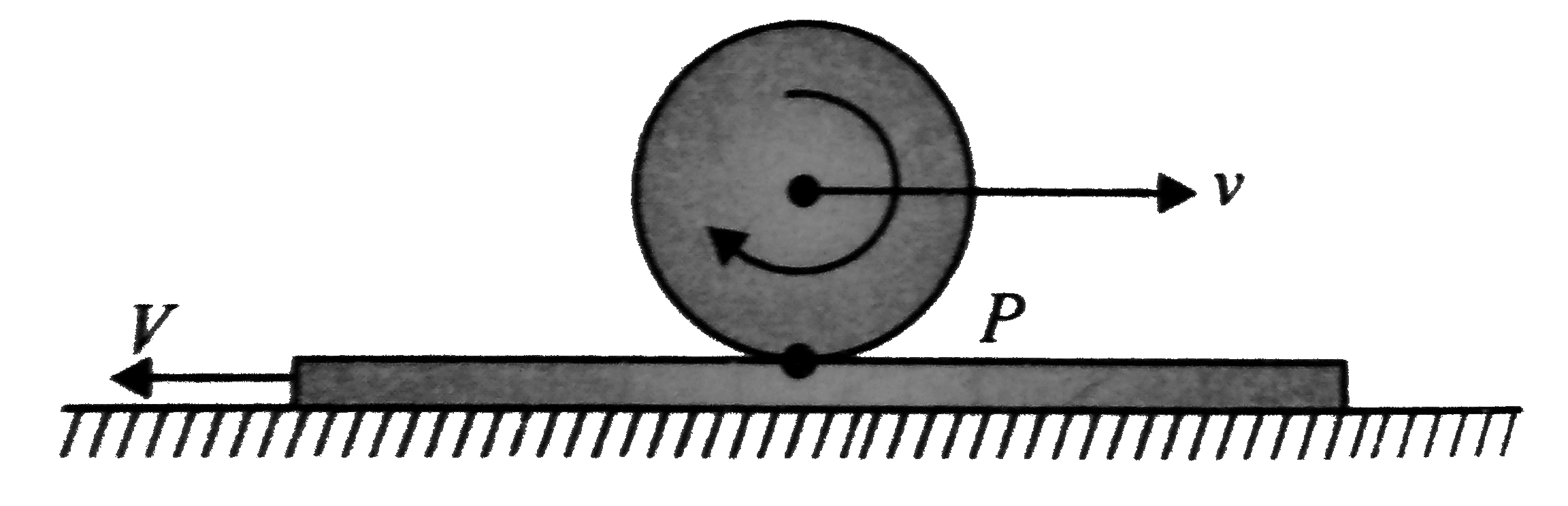
$V_{P} = V = ω R = v$
$(0 + μ >) = (ω_{0} - \frac{5}{2} \frac{μ g}{R} t) R - (0 + μ g t)$
$(2 μ gt + \frac{5}{2} μ gt) = ω_{0} R \Rightarrow \frac{9 μ t}{2} = ω_{0} R$
$\Rightarrow t - \frac{2 ω_{0} R}{9 μ g}$
Velocity of the plane when rolling starts
$V = 0 + μ gt$
$V_{plank} = μ g \times \frac{2 ω_{0} R}{9 μ g} = \frac{2}{9} ω_{0} R$
velocity of the sphere when rolling starts
$V_{sphere} = 0 + μ g t = \frac{2}{9} ω_{0} R$

Updated on:21/07/2023

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Knowledge Check

A long horizontal plank of mass $m$ is lying on a smooth horizontal surface. A sphere of same mass $m$ and radius $r$ is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is $μ$ . After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the velocity of the sphere after the pure rolling starts
A $\frac{2 ω_{0} r}{9}$
B $\frac{ω_{0} r}{9}$
C $\frac{ω_{0} r}{3}$
D $\frac{2 ω_{0} r}{3}$
A long horizontal plank of mass $m$ is lying on a smooth horizontal surface. A sphere of same mass $m$ and radius $r$ is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is $μ$ . After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
A $\frac{ω_{0}^{2} r^{2}}{81 μ g}$
B $\frac{2}{27} \frac{ω_{0}^{2} r^{2}}{μ g}$
C $\frac{4}{81} \frac{ω_{0}^{2} r^{2}}{μ g}$
D $\frac{2}{81} \frac{ω_{0}^{2} r^{2}}{81 μ g}$
Assertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say $ω_{0}$ . Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.
AIf both Assertion and Reason are correct and Reason is the correct explanation of Assertion
BIf both Assertion and Reason are true but Reason is not the correct explanation of Assertion
CIf Assertion is true but Reason is fasle
DIf Assertion is false but Reason is true