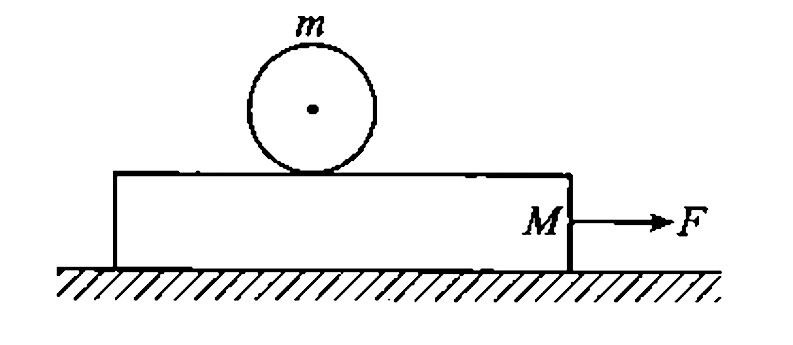
Find the acceleration of a system consisting of a cylinder of mass m and radius R and a plank of mass M placed an a smooth surface if it is pulled with a force F as shown Fig. Given that sufficient friction is present between the cylinder and the plank surface to prevent sliding of the cylinder.

F−T−f=Ma……i
T−f=Ma…………ii
α=fR12mR2=2fmR…….iii
Constraint relation aplank=aP
Rα−a=a
or Rα=2a……iv

Solving these equations, we get
a=F3m+M
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.4
13 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective
19 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.2
13 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICSCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
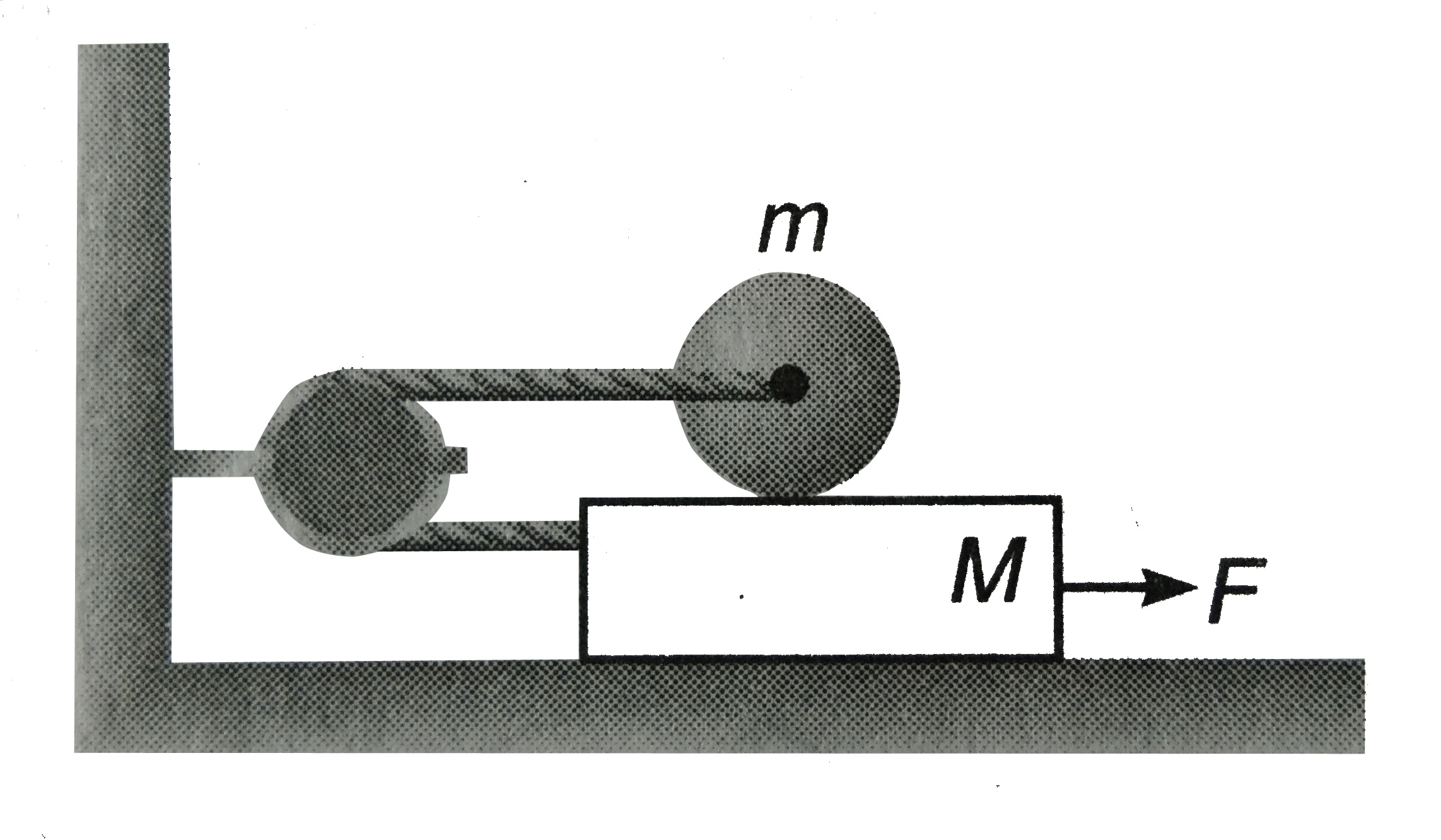
Find the acceleration of the cylinder of mass m and radius R and that of plank of mass M placed on smooth surface if pulled with a force F as shown in figure. Given that sufficient friction is present between cylinder and the plank surface to prevent sliding of cylinder.
View SolutionA solid cylinder of mass m and radius R rest on a plank of mass 2m lying on a smooth horizontal surface. String connecting cylinder to the plank is passing over a massless pulley mounted on a movable light block B and the friction between the cylinder and the plank is sufficient to prevent slipping. if the block B is pulled with a constant forceF, the acceleration of the plank is 2Fxm then calculate x.

View Solution
Knowledge Check
Consider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.
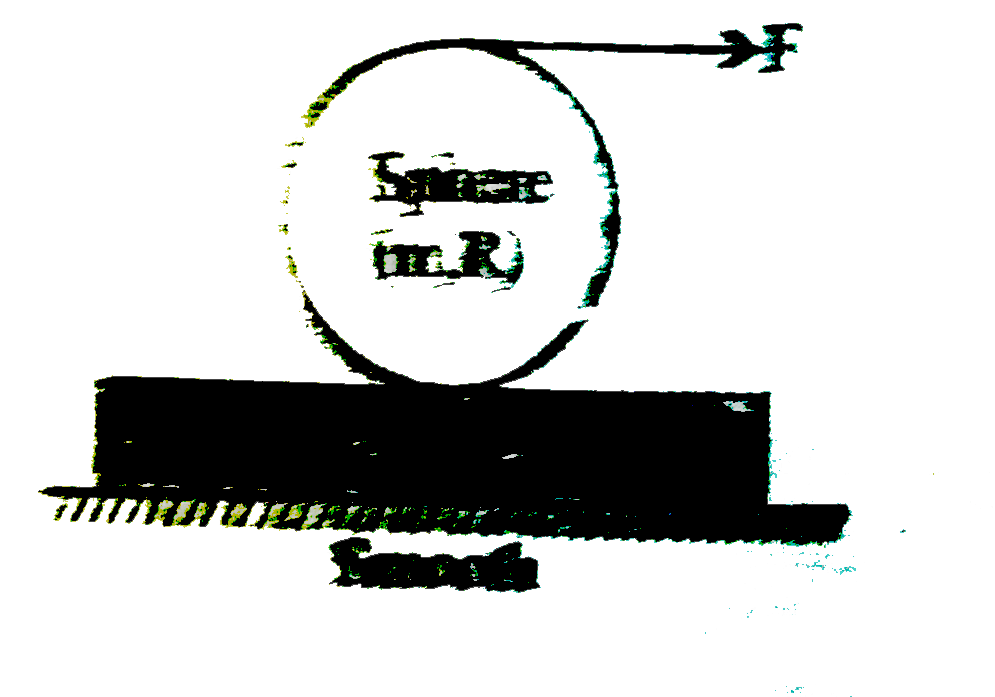
Acceleration of the plank isA3F16mB11F8mC9F4mDZeroConsider the system shown. A solide sphere (of mass m and radius R) is placed over a plak (of mass 2m and placed over a smooth horizontal surface.) A horizontal force F is applied at the top of the sphere, as shown. Consider that the friction between the sphere and plank is sufficient enough for no slipping of the sphere over then plank.

Friction force acting between the sphere and the plank isAF8B3F8C5F8D7F8A uniform cylinder of mass m lies on a fixed plane inclined at a angle θ with the horizontal. A light string is tied to the cylinder at the rightmost point, and a mass m hangs from the string as shown. Assume that the coefficient of friction between the cylinder and the incline plane is sufficiently large to prevent slipping. for the cylinder to remain static the value of m is
 AMsinθ1−sinθBMcosθ1+sinθCMsinθ1+sinθDMcosθ1−cosθ
AMsinθ1−sinθBMcosθ1+sinθCMsinθ1+sinθDMcosθ1−cosθ
Find the moment of inertia of a solid cylinder of mass M and radius R about a line parallel to the axis of the cylinder and on the surface of the cylinder.
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

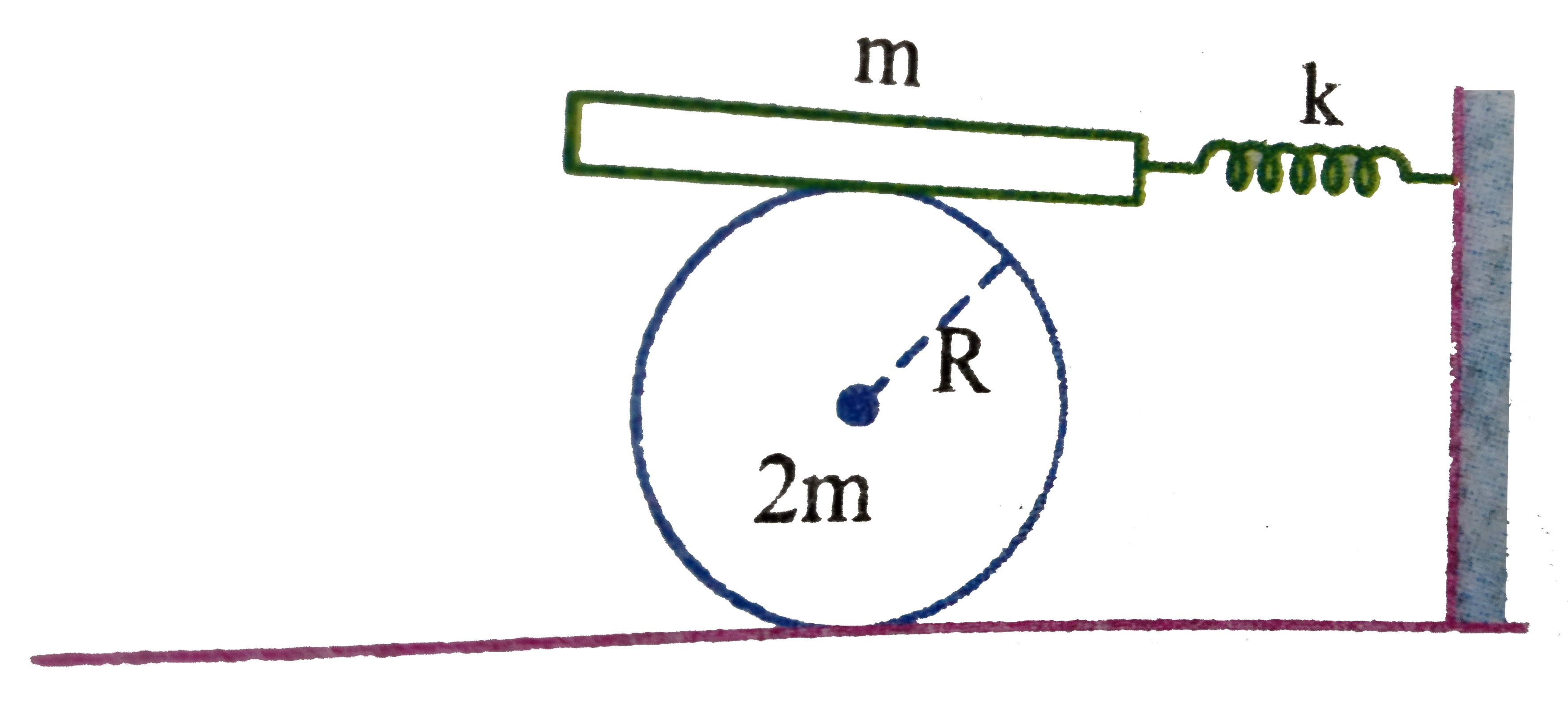
View SolutionA uniform plank of mass m=1kg, free to move in the horizontal direction only, is placed at the top of a solid cylinder of mass 2m and radius R. The plank is attched to a fixed wall by means of light spring of spring constant k=7N/m2. There is no slipping between the cylinder and the plank, and between the cylinder and the ground. the angular frequency of small oscillations of the system is
View SolutionA plank of mass M is placed on a smooth surface over which a cylinder of mass m and radius R is placed as shown in figure-5.63. Now the plank is pulled towards right with an external force F. If cylinder does not slip over the surface of plank find the linear acceleration of plank and cylinder and the angular acceleration of the cylinder.
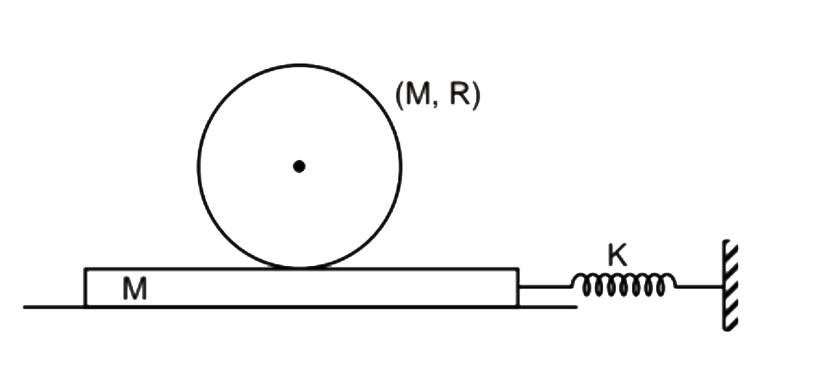
View SolutionA cylinder of mass M and radius R lies on a plank of mass M as shown. The surface between plank and ground is smooth, and between cylinder and plank is rough. Assuming no slipping between cylinder and plank, the time period of oscillation (When displaced from equilibrium) of the system is
View Solution
