A wheel is rolling without slipping on a horizontal plane with velocity $v$ and acceleration $a$ of centre of mass as shown in figure. Acceleration at

A

A is vertically upwards

B

B may be vertically downwards

C

C cannot be horizontal

D

A point on the rim may be horizontal leftwards.

Video Solution

Text Solution

Verified by Experts

Net acceleration of any point on the rim is vector sum of $a, R ω^{2}$ and $R α$ with $a = R α$
$a_{A} = R ω^{2} \to$ vertically upwards
if $a = R ω^{2}, a_{B}$ is vertically downwards and so on.

Updated on:21/07/2023

|

Class 11 PHYSICS RIGID BODY DYNAMICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

A wheel is rolling on a horizontal plane. At a certain instant it has a velocity $v$ and acceleration $a$ of $C M$ as shown in figure . Acceleration of

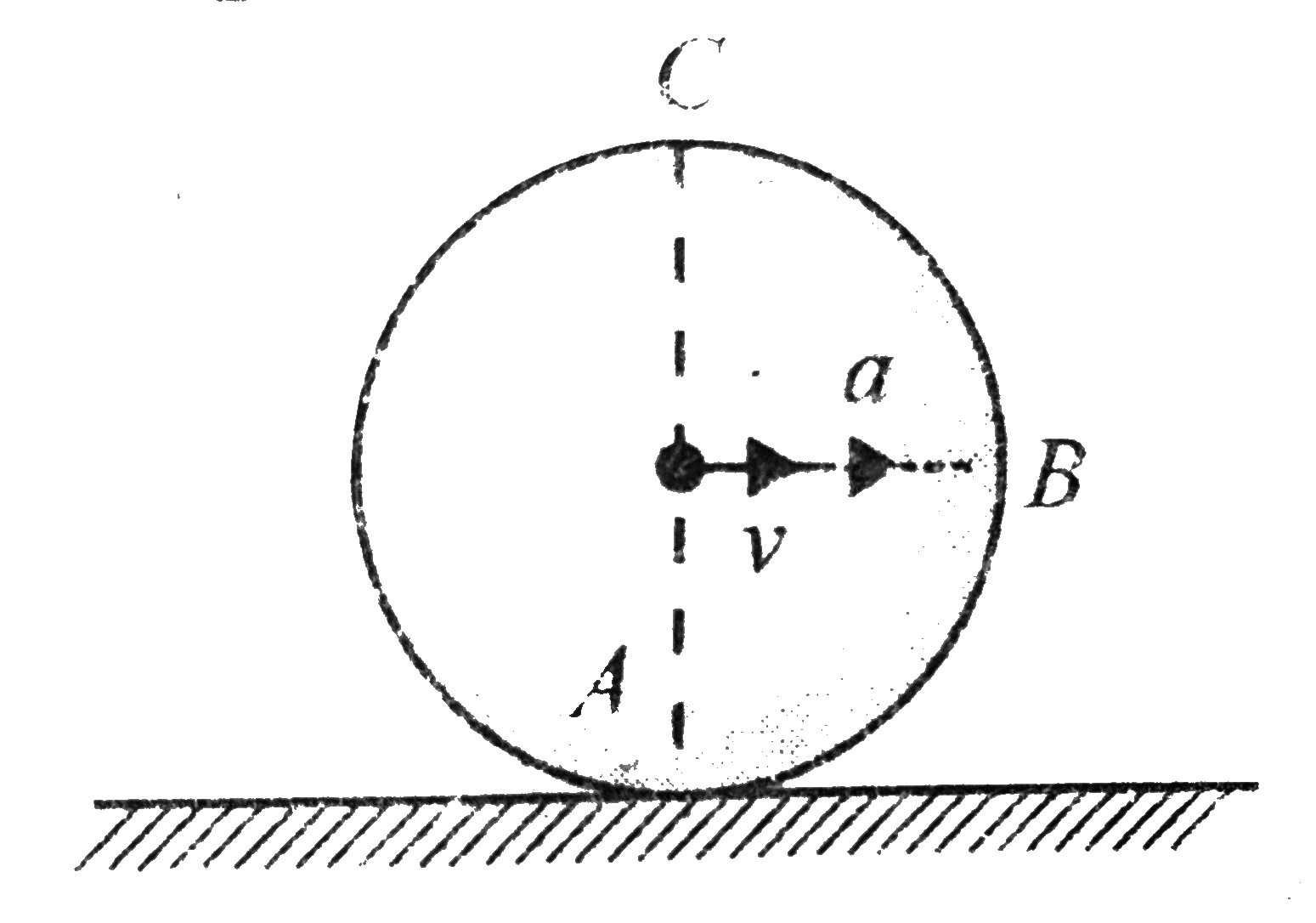A $A$ is vertically upwards
B $B$ may be vertically down-wards
C $C$ cannot be horizontal
Dsome point on the rim may he horizontal leftwards
A disc having radius $R$ is rolling without slipping on a horizontal ( $x - z$ ) plane. Centre of the disc has a velocity $v$ and acceleration $a$ as shown.
Speed of point $P$ having coordinates $(x, y)$ is
A $\frac{v \sqrt{x^{2} + y^{2}}}{R}$
B $\frac{v \sqrt{x^{2} + {(y + R)}^{2}}}{R}$
C $\frac{v \sqrt{x^{2} - {(y - R)}^{2}}}{R}$
Dnone
A disc having radius $R$ is rolling without slipping on a horizontal ( $x - z$ ) plane. Centre of the disc has a velocity $v$ and acceleration $a$ as shown.
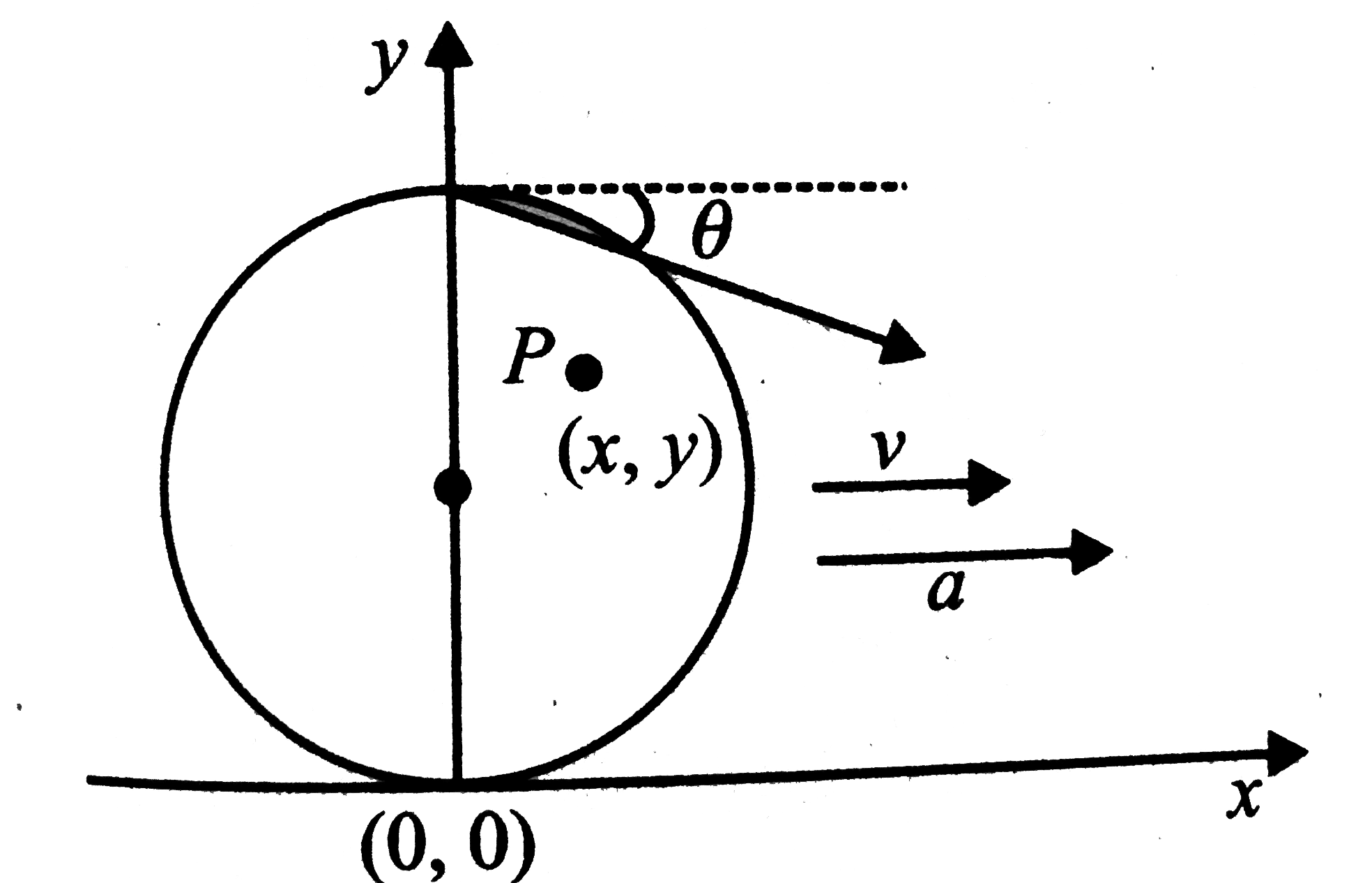
If $v = \sqrt{2 a R}$ the angle $ρ$ between acceleration of the top most point and the horizontal is
A $0$
B $45^{\circ}$
C ${tan}^{- 1} (2)$
D ${tan}^{- 1} (\frac{1}{2})$

DC PANDEY-ROTATIONAL MECHANICS-Level 2 Multiple Correct

Home
Ask Doubt
Profile