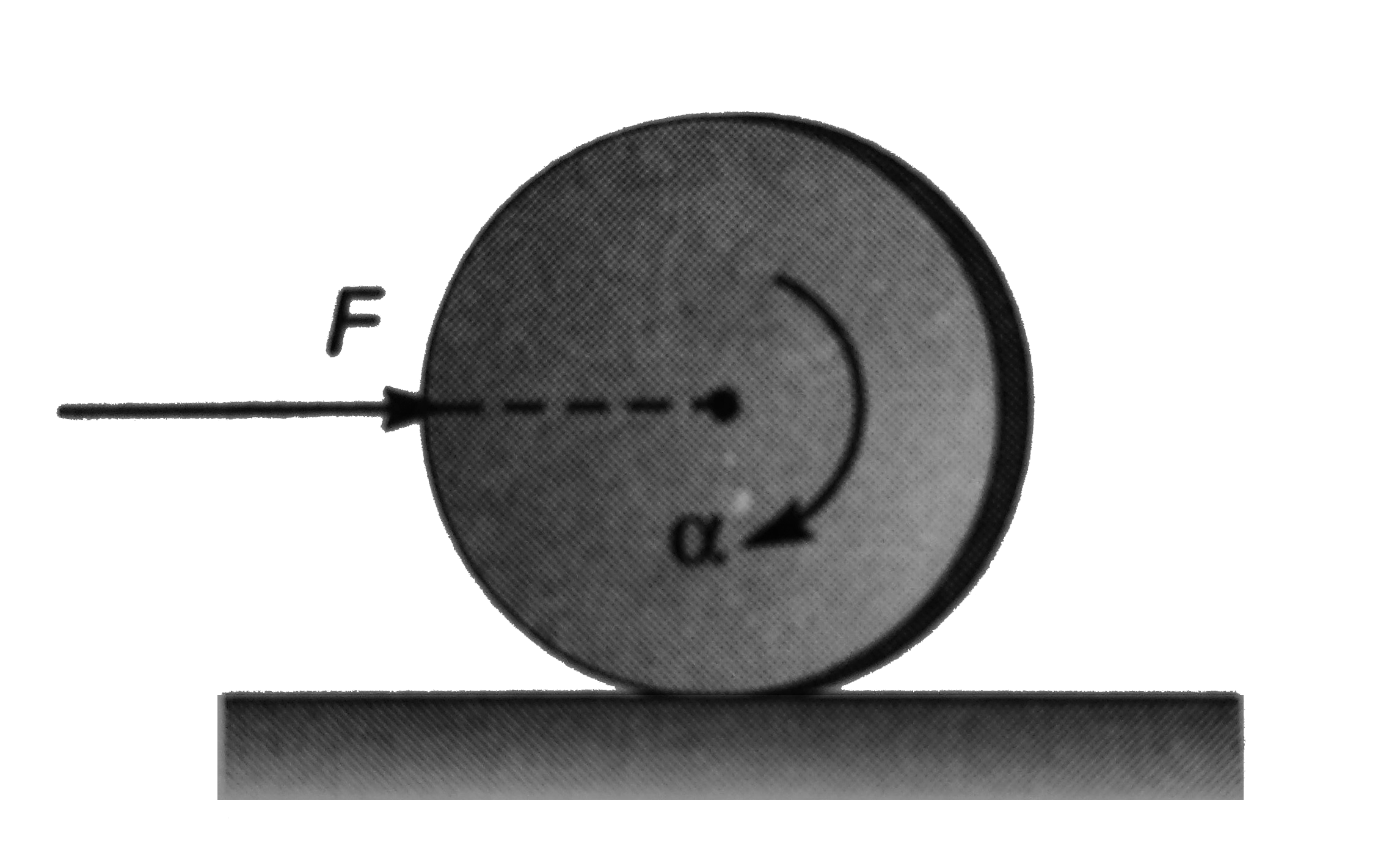
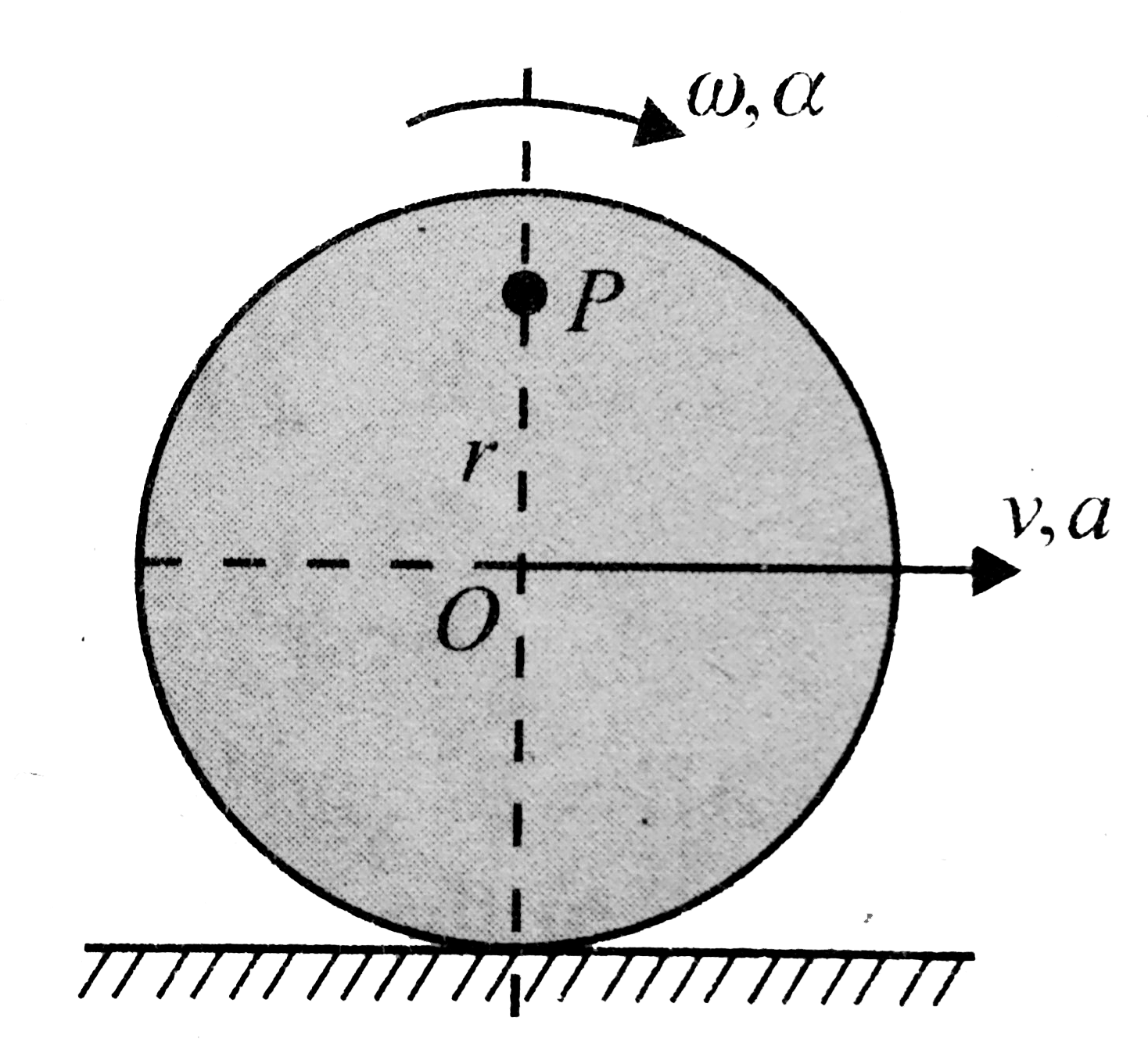
Consider a uniform disc of mass $m$ , radius $r$ rolling without slipping on a rough surface with linear acceleration $a$ and angular acceleration $α$ due to an external force F as shown in the figure coefficient of friction is $μ$ .
Q. Angular momentum of the disc will be conserved about

centre of mass

point of contact

a point at a distance $3 R / 2$ vertically above the point of contact

a point at a distance $4 R / 3$ vertically above the point of contact.

Video Solution

Text Solution

Verified by Experts

About point P net torque of F and f is zero. So, angular momentumj is conserved.

Updated on:21/07/2023

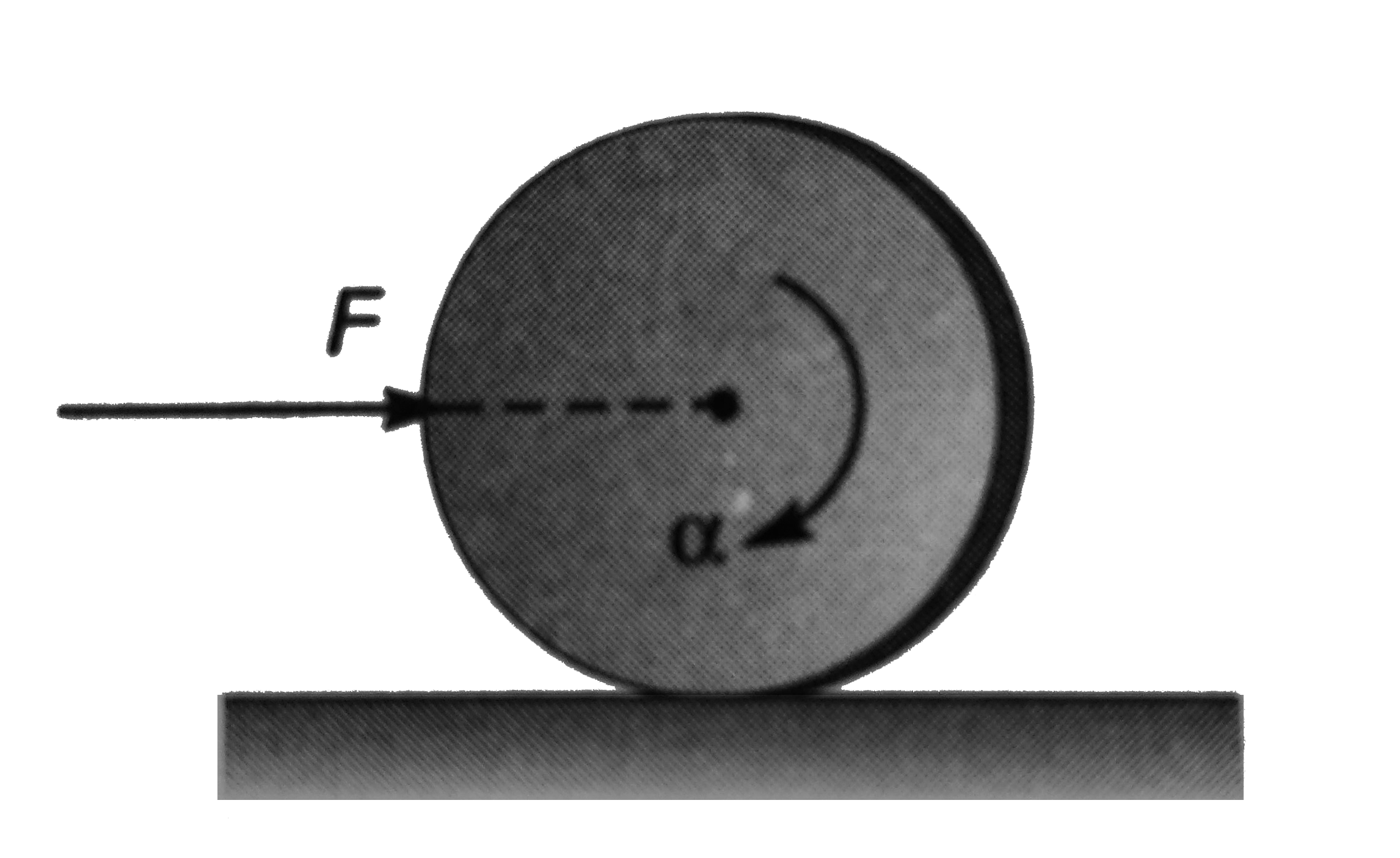
Consider a uniform disc of mass $m$ , radius $r$ rolling without slipping on a rough surface with linear acceleration $a$ and angular acceleration $α$ due to an external force F as shown in the figure coefficient of friction is $μ$ .
Q. The magnitude of frictional force acting on the disc is
A $m a$
B $μ m g$
C $\frac{m a}{2}$
Dzero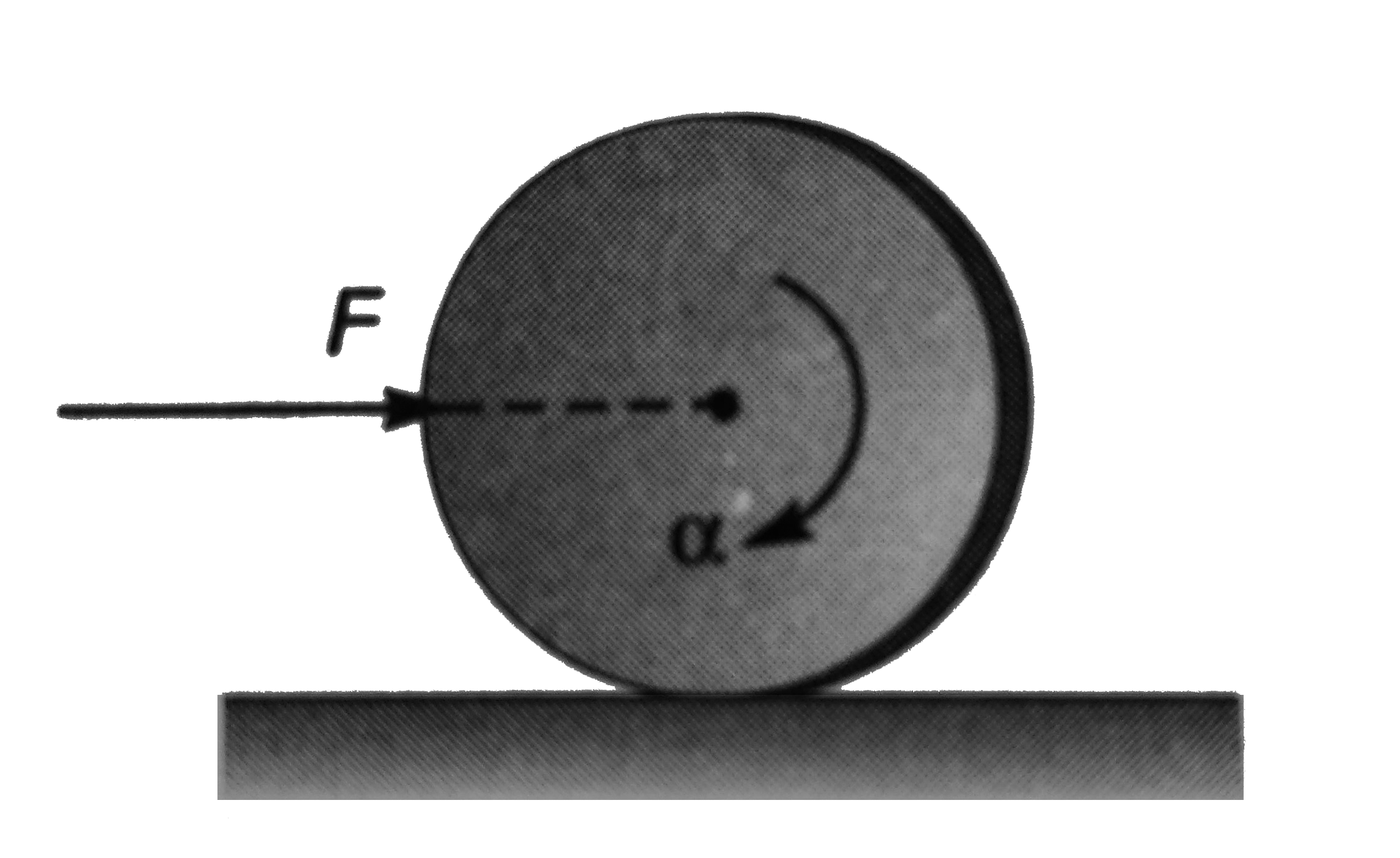
Consider a uniform disc of mass $m$ , radius $r$ rolling without slipping on a rough surface with linear acceleration $a$ and angular acceleration $α$ due to an external force F as shown in the figure coefficient of friction is $μ$ .
Q. The work done by the frictional force at the instant of pure rolling is
A $\frac{μ m g a t^{2}}{2}$
B $μ m g a t^{2})$
C $μ m \frac{g (a t^{2})}{α}$
Dzero
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/R
BContinuously increasing
CDependent on mass M
DIndependent of radius (R)