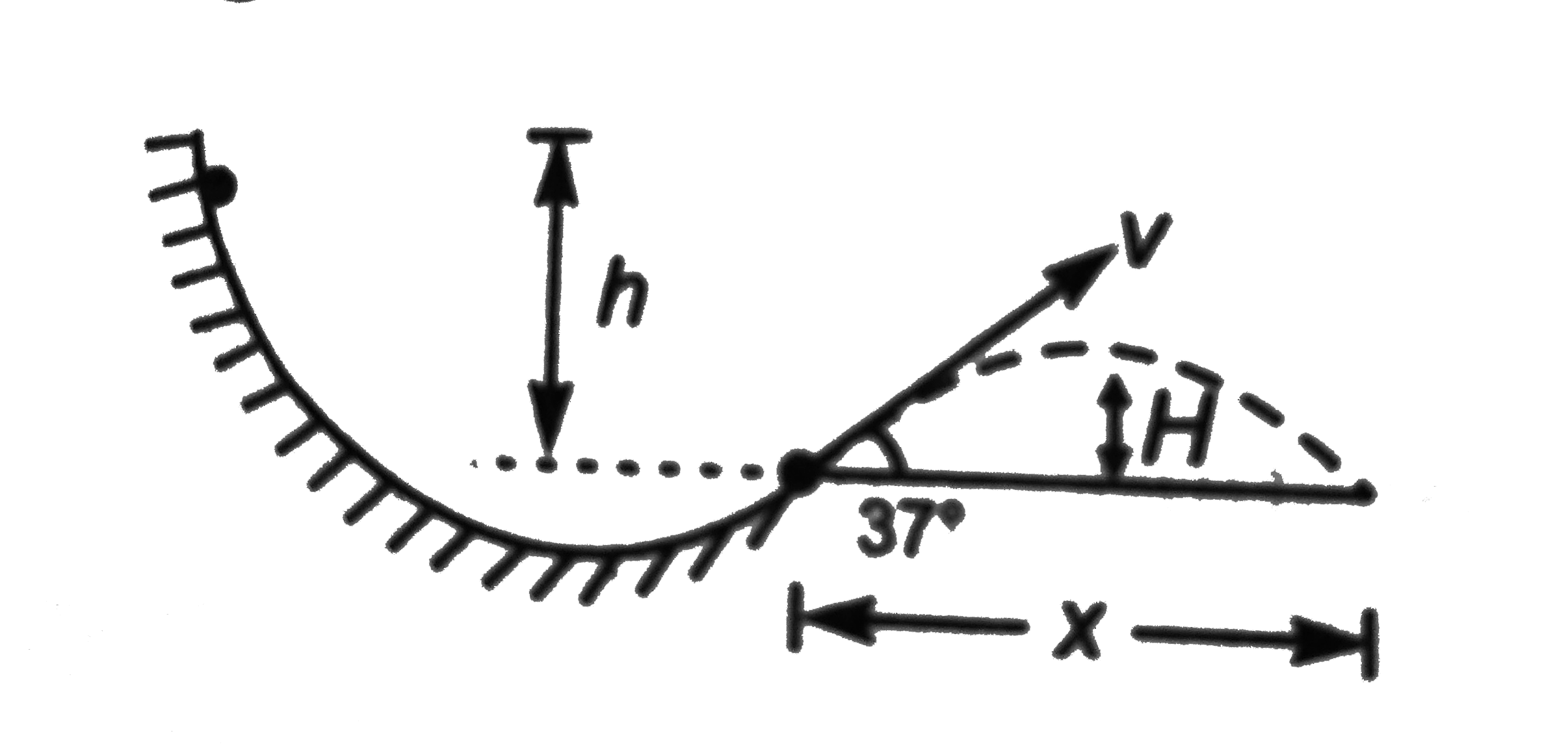
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection is
after falling a height is mgh
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2
1 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective
36 Videos
- ROTATIONAL MECHANICSBOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct
26 Videos
- ROTATIONBOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises
39 Videos
- ROTATIONAL MOTIONBOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions
17 Videos
Similar Questions
A ball is projected from the ground at angle θ with the horizontal. After 1s, it is moving at angle 45∘ with the horizontal and after 2s it is moving horizontally. What is the velocity of projection of the ball ?
View SolutionA ball was thrown by a boy a at angle 60∘ with horizontal at height 1 m from ground. Boy B is running in the plane of motion of ball and catches the ball at height 1 m from ground. He finds the ball falling vertically. If the boy is running at a speed 20 km/hr. Then the velocity of projection of ball is-
View Solution
Knowledge Check
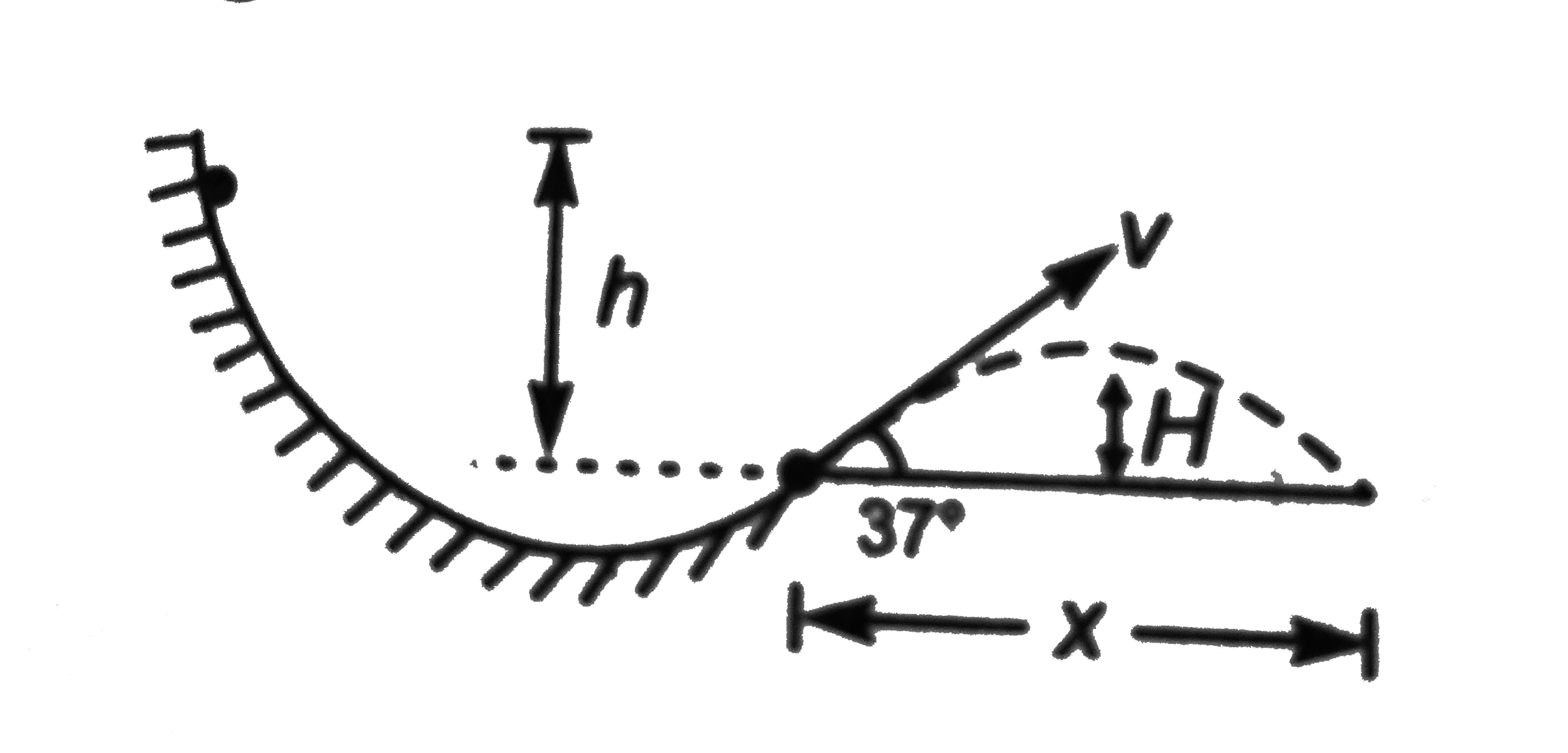
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball isA144125hB4825hC4835hD247h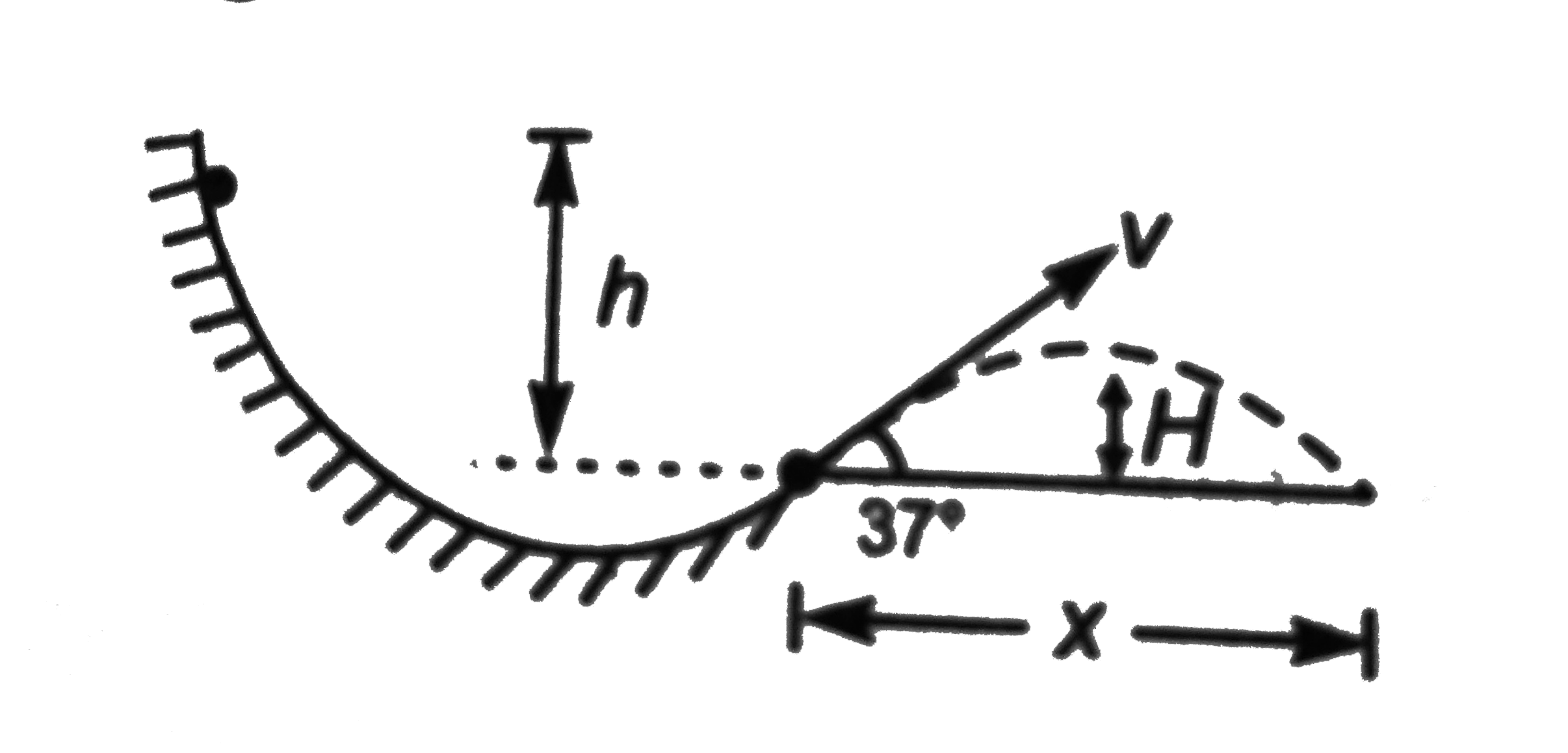
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground isA9h35B18h35C18h25D27h125A ball is projected horizontal from the top of a tower with a velocity v0. It will be moving at an angle of 60∘ with the horizontal after time.
Av0√3gB√3v0gCv0gDv0g
From the top of a tower 20m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:
View SolutionFrom the the top of a tower 19.6 m high, a ball is thrown horizontally. If the line joining the point of projection to the point where it hits the ground makes an angle of 45∘ with the horizontal, then the initial velocity of the ball is:-
View SolutionA ball is thrown horizontally from a cliff such that it strikes the ground after 5s.The line of sight makes an angle 37∘ with the horizontal.The initial velocity of projection in ms−1 is
View SolutionFrom the top of a building 80mhigh, a ball is thrown horizontally which hits the ground at a distance.The line joining the top of the building to the point where it hits the ground makes an angle of 45∘ with the ground. Initial velocity of projection of the ball is (g=10m/s2)
View SolutionA tennis ball is thrown upward at an angle from point A. It follows a parabolic trajectory and hits the ground at point D. At the instant shown, the ball is at point B. Point C represents the highest position of the ball above the ground.
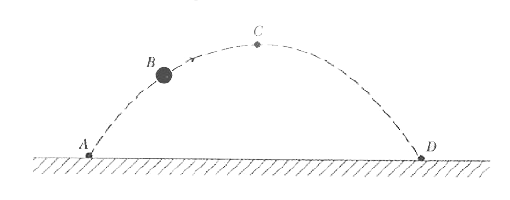
While in flight, how do the x and y components of the velocity vector of the ball compare at the points A and D?
View Solution
