A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having velocity of 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Then

I1ω1=I2ω2
∴ω2=I1I2ω1
=(1/2mR2)(1/2mR2+mR2).ω
=ω3
Pi=mvi=m(2ωR)=2mωR
Pf=mvf=m(ω3R)=13mωR
impulse J=∣∣Pf−Pi∣∣
=√P2i+P2f (as θ=90∘)
=√373mωR
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 21videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective36videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A uniform dis of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same mass m and having 2ωR towards centre of the disc collides with the disc moving horizontally and sticks to its rim. Find
(A) the angular velocity of the disc.
(B) the impulse on the particle due to disc
( C) the impulse on the disc due to hinge.View SolutionA solid sphere of radius r and mass m rotates about an axis passing through its centre with angular velocity ω. Its K.E. Is
View Solution
Knowledge Check
- Question 1 - Select One
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim. The impulse on the particle due to the disc is
A√173mωRB√353mωRC√373mωRD√293mωR - Question 2 - Select One
A uniform disc of mass m and radius R rotates about a fixed vertical axis passing through its centre with angular velocity ω. A particle of same angular velocity mass m and moving horizontally with velocity 2ωR towards centre of the disc collides and sticks to its rim.
The angular velocity of the disc after the particle sticks to it isAω5Bω3Cω2Dω4 - Question 3 - Select One
A uniform disc of mass M and radius R is rotating about a horizontal axis passing through its centre with angular velocity ω . A piece of mass m breaks from the disc and flies off vertically upwards. The angular speed of the disc will be
A(M−2m)ω(M−m)B(M+2m)ω(M+m)C(M−2m)ω(M+m)D(M+2m)ω(M−m)
A uniform disc of mass m and radius R I rotated about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficnet of friction between te disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.View SolutionA uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
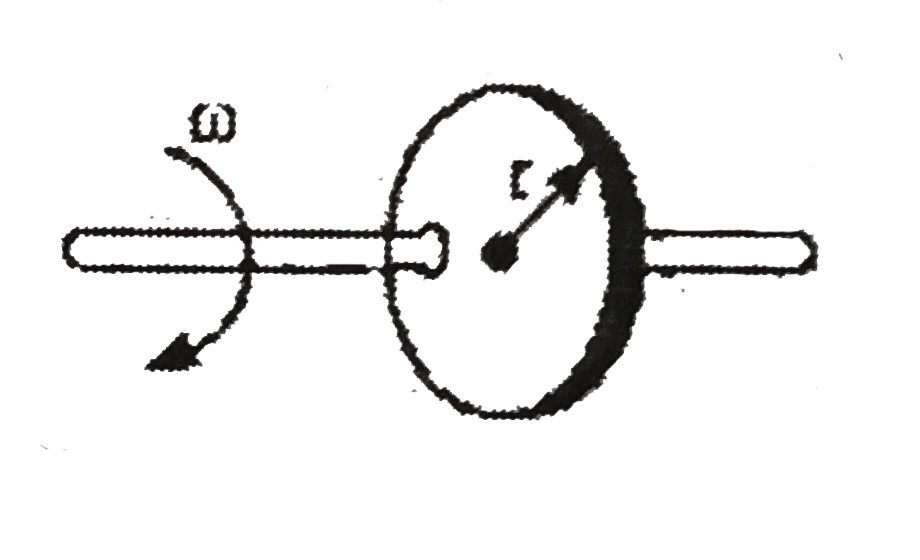 View Solution
View SolutionA uniform disk of mass 300kg is rotating freely about a vertical axis through its centre with constant angular velocity ω. A boy of mass 30kg starts from the centre and moves along a radius to the edge of the disk. The angular velocity of the disk now is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω . Another disc of same dimensions but of mass 14 M is placed gently on the first disc co-axially. The angular velocity of the system is
View SolutionA thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions but of mass M/4 is placed gently on the first disc coaxially. The angular velocity of the system now is
View Solution

