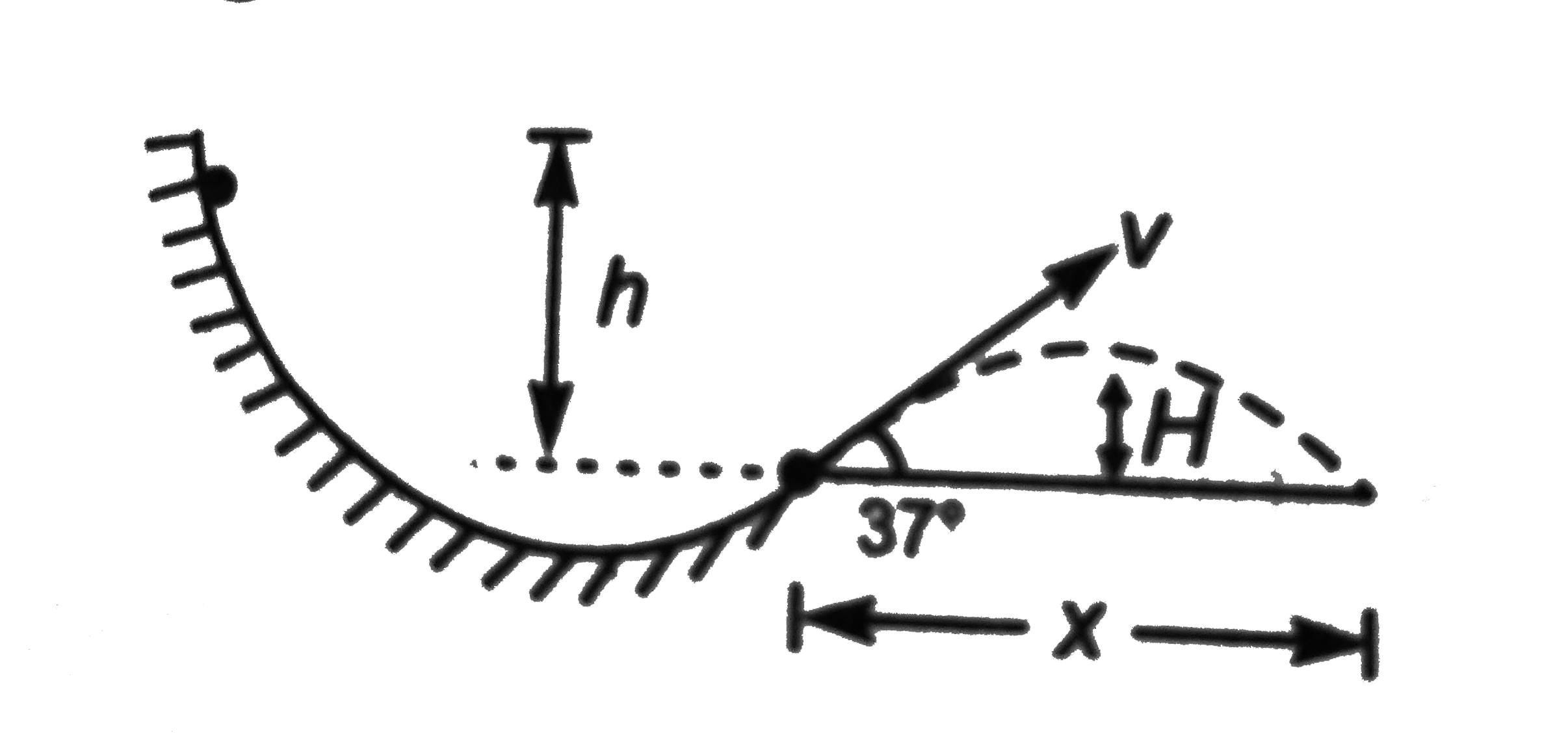
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Maximum height reached by ball H above ground is
9h35
18h35
18h25
27h125
H=v2sin2sin37∘2g
=(6gh/5)(3/5)22g=27h125
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 21videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Subjective36videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MECHANICSEXERCISE - Level 2 Single Correct26videos
ROTATIONAL MECHANICS
- BOOK - DC PANDEYCHAPTER - ROTATIONEXERCISE - (C) Chapter Exercises39videos
ROTATION
- BOOK - DC PANDEYCHAPTER - ROTATIONAL MOTIONEXERCISE - Integer Type Questions17videos
ROTATIONAL MOTION
Similar Questions
A ball is thrown horizontally and at the same time another ball is dropped down from the top of a tower Will both the balls reach the ground at the same time ?
View SolutionA tennis ball is thrown from a height h above the ground.If the coefficient of restitution is e,what height will the ball achieve after the third collision? "
View Solution
Knowledge Check
- Question 1 - Select One
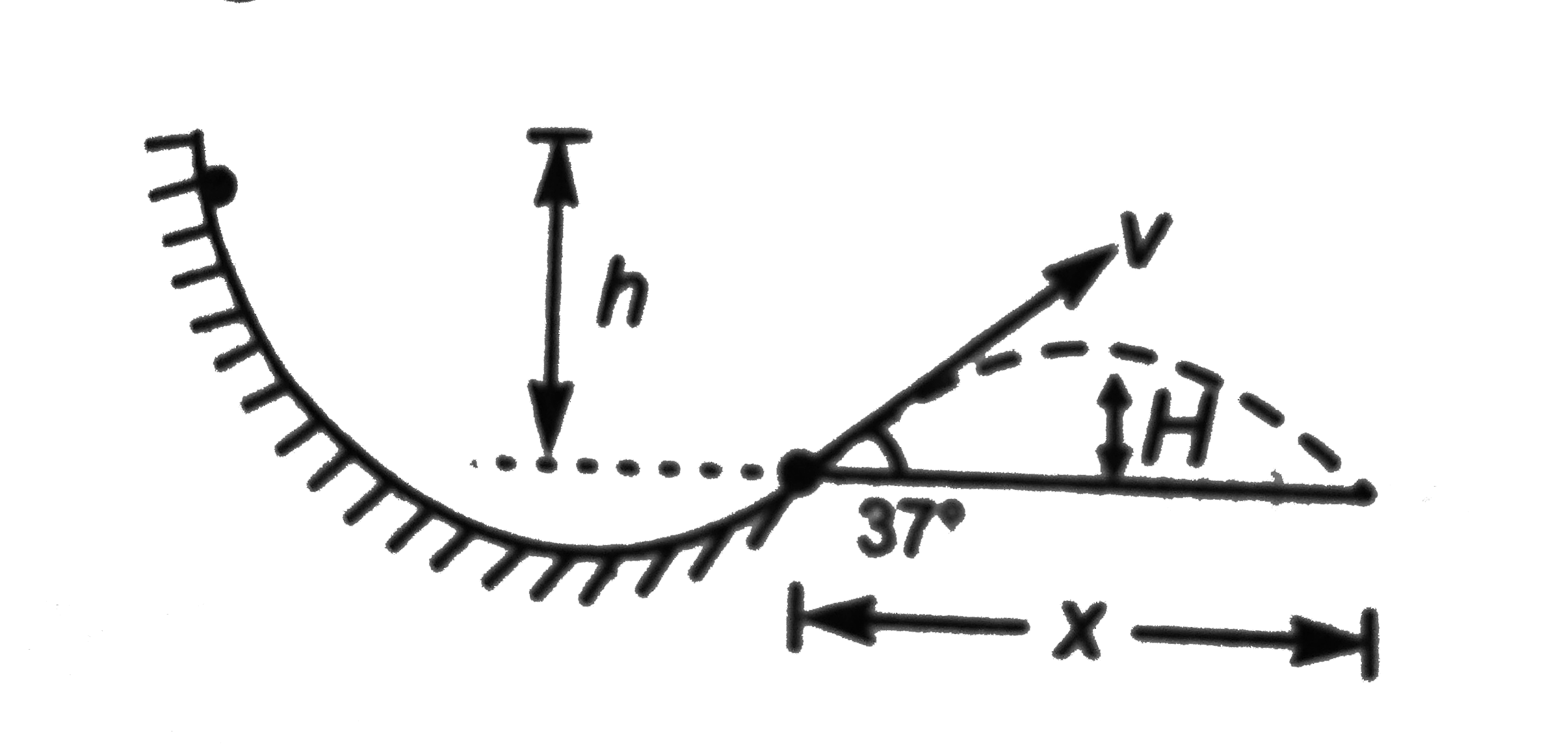
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. Range x of the ball isA144125hB4825hC4835hD247h - Question 2 - Select One
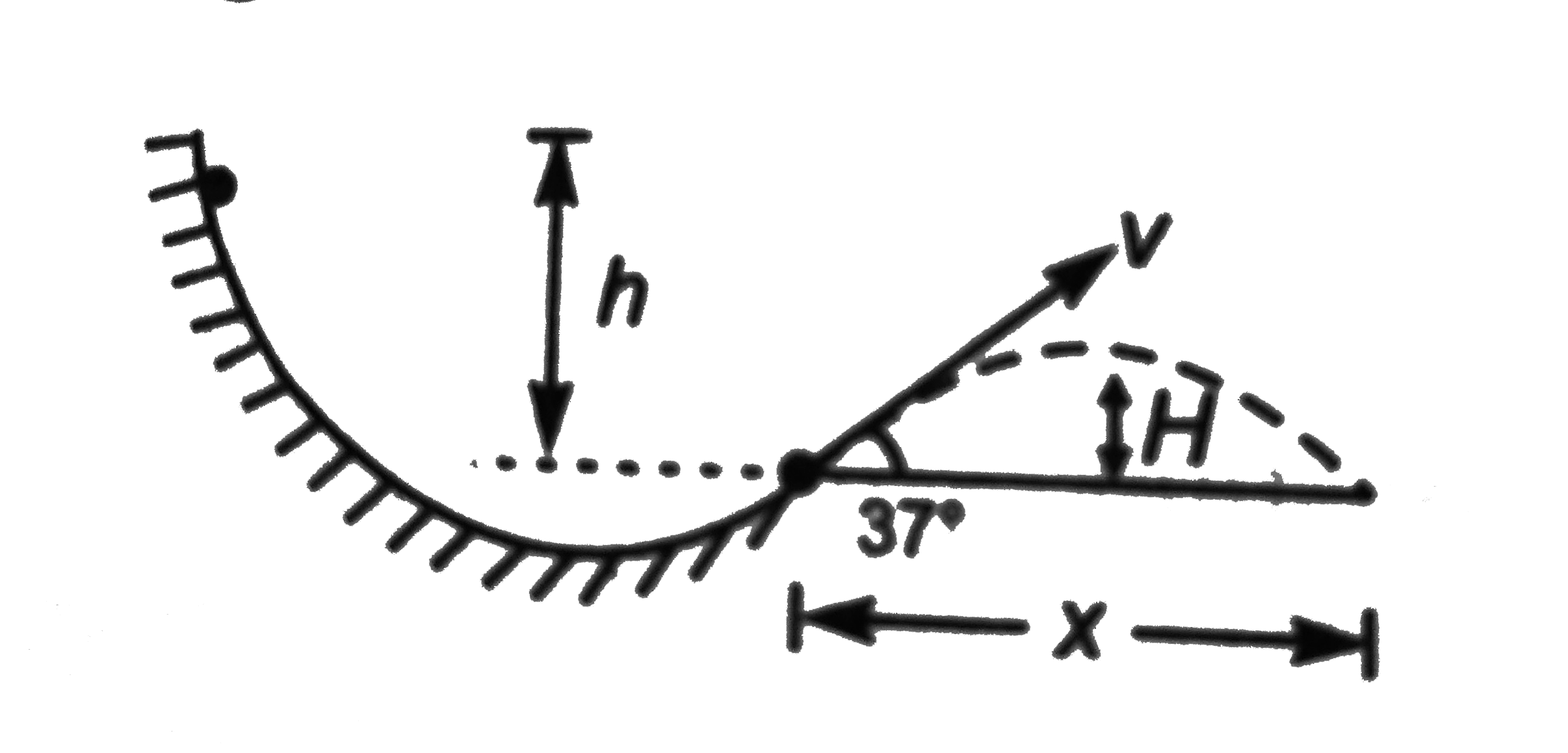
A tennis ball, starting from rest, rolls down the hill in the drawing. At the end of the hill the ball becomes airborne, leaving at an angle of 37∘ with respect to the ground treat the ball as a thin-walled spherical shell.
Q. The velocity of projection v isA√2ghB√107ghC√57ghD√65gh - Question 3 - Select One
A ball released from rest from the roof of a building of height 45 m at t = 0. Find the height of ball from ground at t = 2s.
A10 mB20 mC25 mD30 m
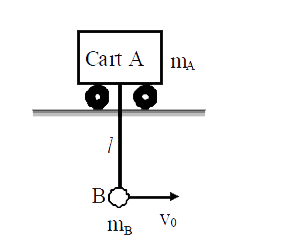
A ball B is suspended from a string of length l attached to a cart A, which may roll on a frictionless surface. Initially the cart is at rest and the ball is given a horizontal velocity v0. Determine
the maximum height reached by the ball.
 View Solution
View SolutionSoumya throws a ball upwards, from a rooftop, 80 m above. It will reach a maximum height and then fall back to the ground. The height of the ball from the ground at time 't' is 'h', which is given by h=−16t2+64t+80

What is the maximum height reached by the ball ?View SolutionA tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
View SolutionA tennis ball is released from height h above ground level. If the ball makes inelastic collision with the ground, to what height will it rise after third collision
View SolutionA small boy is throwing a ball towards a wall 6 in front of him. He releases the ball at a height of 1.4 m from the ground. The ball bounces from the wall at a height of 3 m, rebounds from the ground and reaches the boys hand exactly at the point of release. Assuming the two bounces (one from the wall and the other from the ground) to be perfectly elastic, how far ahead of the boy did the ball bounce from the ground?
View Solution

