A sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
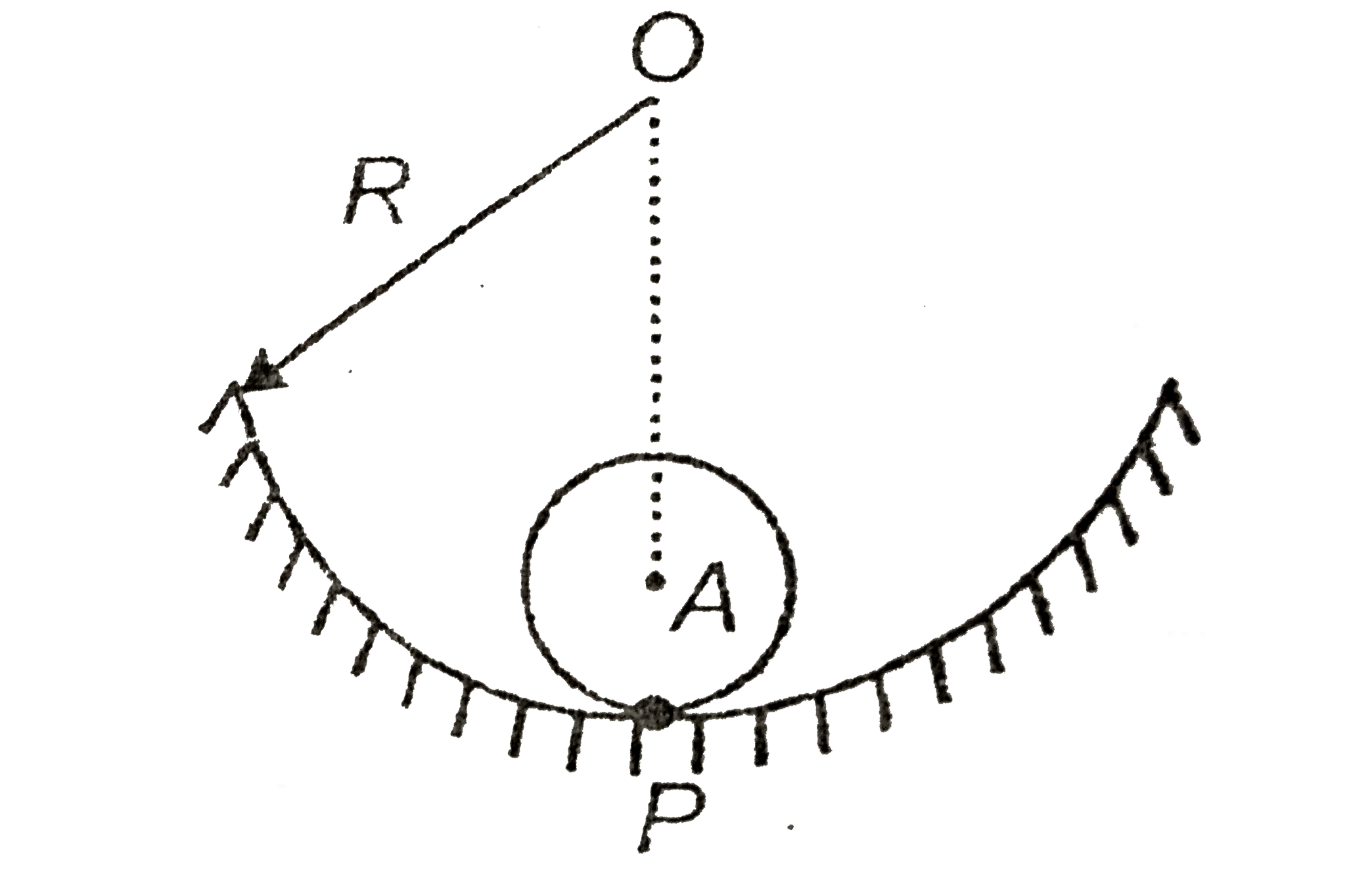
ω2(R−r)Rr
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Try Yourself
Explore 63 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBook:AAKASH INSTITUTEChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTIONExercise:Assignment (Section - I) Subjective Type Questions
Explore 8 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBook:AAKASH INSTITUTEChapter:SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSExercise:Assignment (Section-D (Assertion and reason))
Explore 5 Videos
- TEST 1Book:AAKASH INSTITUTEChapter:TEST 1Exercise:EXERCISE
Explore 9 Videos
Similar Questions
The angular velocity and angular acceleration of the pivoted rod are given as ω and α respectively. Fid the x and y components of acceleration of B.
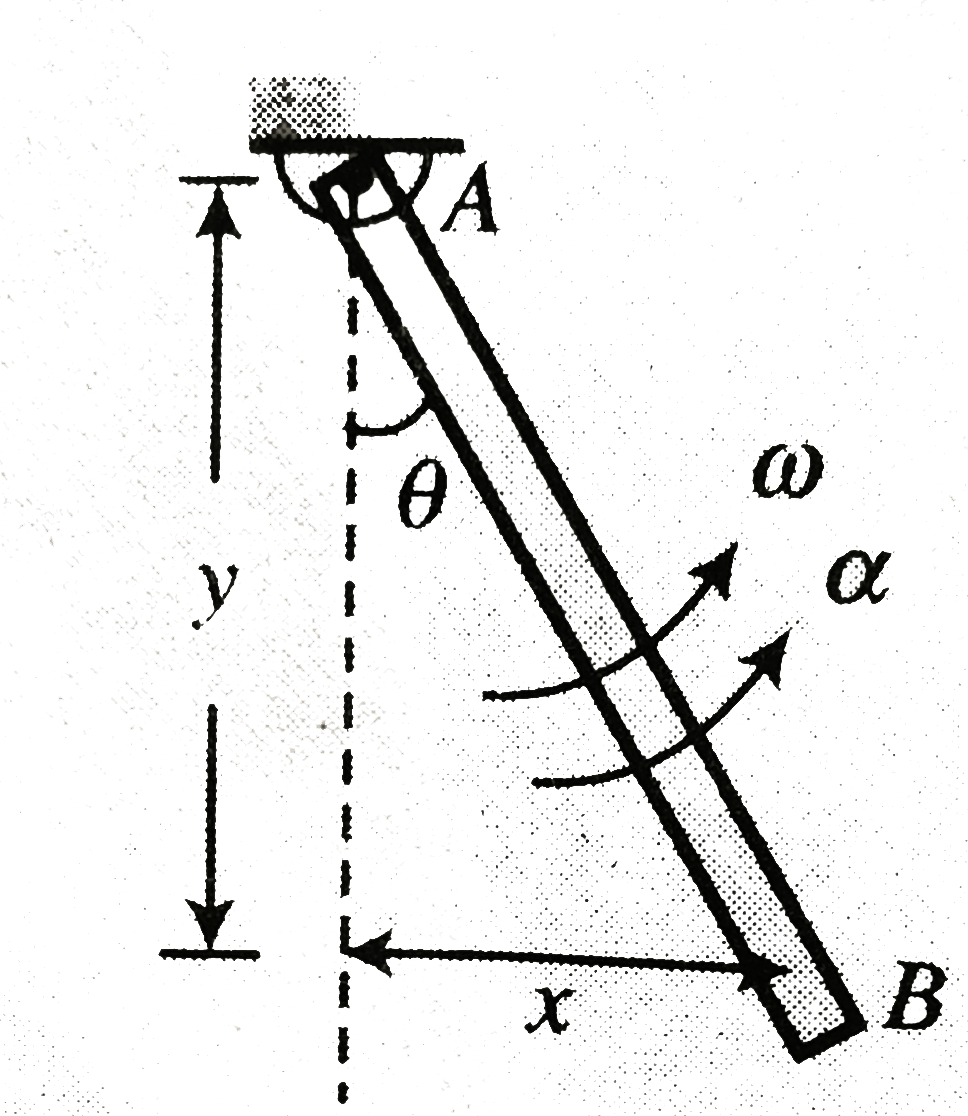
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

View Solution
Knowledge Check
A ball of radius r is rolling (pure rolling) on a convex stationary circular surface of radius R with angular velocity ω and angular acceleration α. The magnitude of vertical acceleration of top point of the ball is
Aω2r(R+2rR+r)Bω2rCω2rR+rDω2rRR+rA symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
Av/RBContinuously increasingCDependent on mass MDIndependent of radius (R)A particle moving along a circule path of radius 'r' with uniform angular velocity ω. Its angular acceleration is
Arω2Br/ωCzeroDω/r

A solid sphere of mass m and radius R is rolling without slipping as shown in figure. Find angular momentum of the sphere about z-axis.
View SolutionA uniform sphere of radius R16 starts rolling down without slipping from the top of another sphere of radius R=1m. The angular velocity of the sphere of in rads−1, after it leaves the surface of the larger sphere is 8xn. Where n=--
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View Solution
A disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity the angle between the velocity ad acceleration vectors of point P is
View SolutionA small sphere S of radius ,r and mass m rolls without slipping, inside a large hemispherical bowl B of radius R as shown in figure. S starts from rest at the top point of the hemisphere
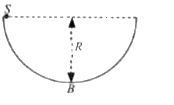
View Solution