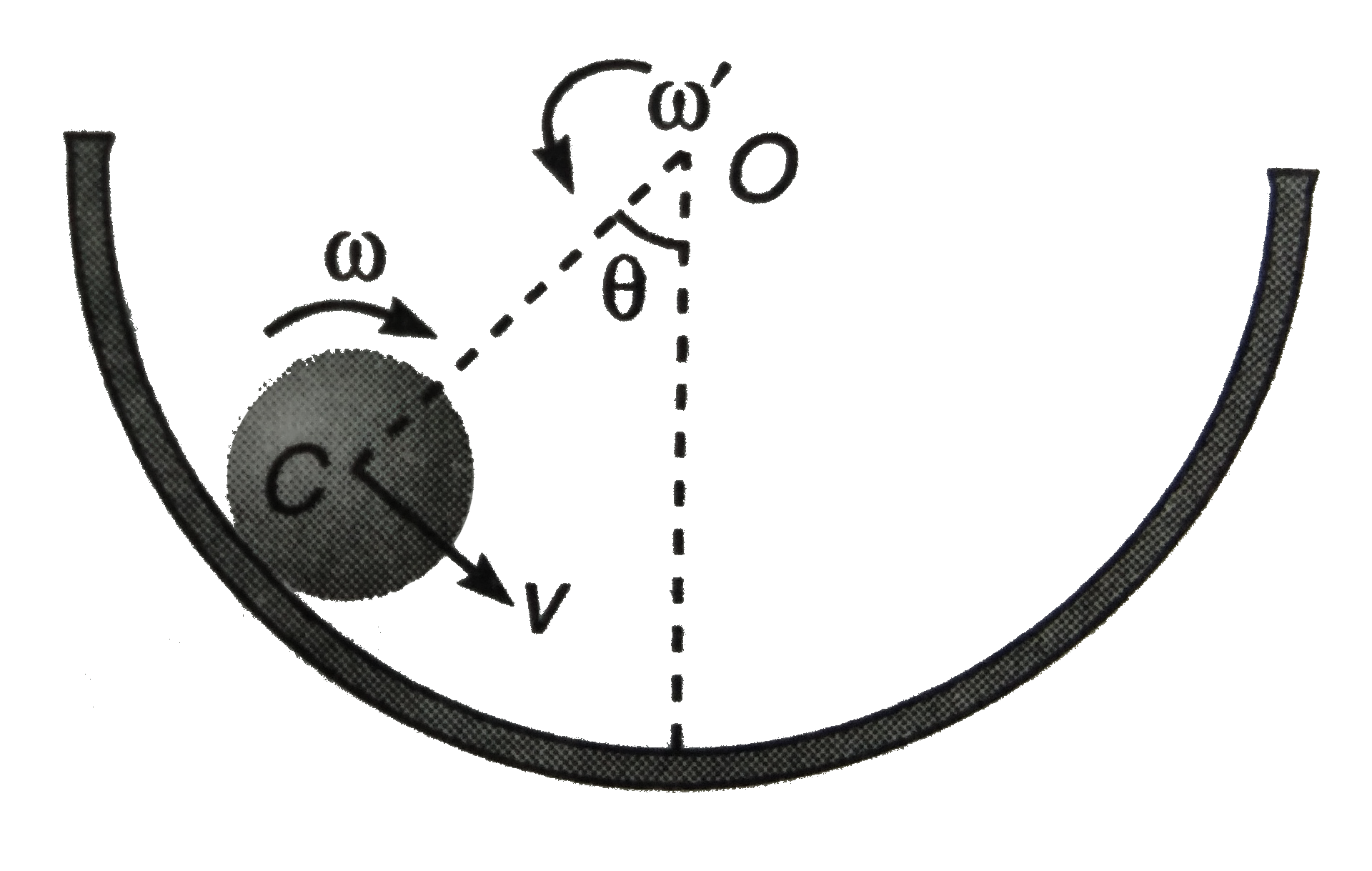
A solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.

The correct Answer is:B
For pure rolling to take place,
v=Rω
ω'= angular velocity of COM of sphere C about O
=v4R=Rω4R=ω4
∴dω'dt=14dωdt
or α'=α4
α=aR for pure rolling
where, a=gsinθ1+ImR2
=5gsinθ7
as, I=25mR2
∴α'=5gsinθ28R
For small θ,sinθ≈θ, being restoring in nature,
α=−5g28Rθ
∴T=2π√∣∣∣θα'∣∣∣
=2π√28R5g
 .
.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 13
3 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
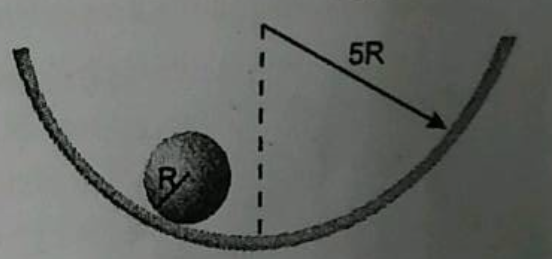
A solid sphere of (radius =R) rolls without slipping in a cylindrical vessel (radius =5R). Find the time period of small of oscillations of the sphere in s−1. Take R=114m and g=10m/s2. (axis is cylinder is fixed and horizontal).
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.

View Solution
Knowledge Check
A small solid sphere of radius r rolls down an incline without slipping which ends into a vertical loop of radius R. Find the height above the base so that it just loops the loop
A52RB52(R−r)C2510(R−r)D2710R−17r10A solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
AThe kinetic energy of rotation is 15mv20.BThe total kinetic energy is 710mv20.CThe mechanical energy (assume the ground as reference) is mgR+710mv20.DAll options are correct.A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
A75gsinθB27gsinθC37gsinθD57gsinθ
A semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is R
View SolutionA spherical ball of mass m and radius r rolls without slipping on a rough concave surface of large radius R. It makes small oscillations about the lowest point. Find the time period.
View SolutionA small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.

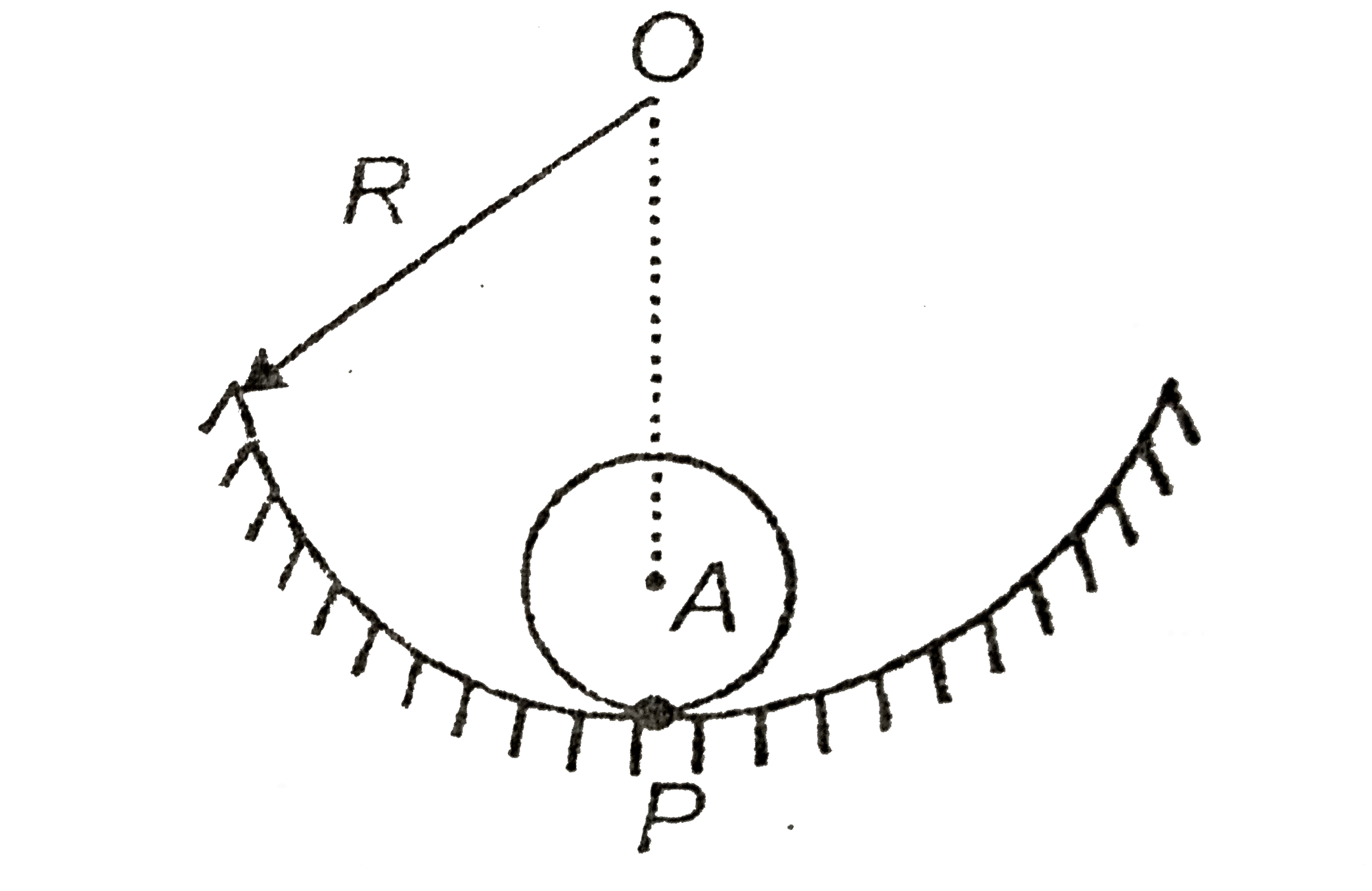
View SolutionA sphere of radius r is rolling without slipping on a hemispherical surface of radius R. Angular velocity and angular acceleration of line OA is ω and α respectively. Find the acceleration of point P on sphere.
View SolutionA ball of radius r is made to oscillate in a bowl of radius R, find its time period of oscillation.
View Solution
