Consider the earth as a uniform sphere if mass M and radius R. Imagine a straight smooth tunnel made through the earth which connects any two points on its aurface. Show that the motion of a particle of mass m along this tunnel under the action of gravitation would be simple harmonic. Hence, determine the time that a particle would take to go from one end to the other through the tunnel.
The correct Answer is:C
Suppose at some instant, the particle is at radial distance r from centre of earth O. Since, the particle is constrained to move along the tunnel, we define its position as distance x from C. Hence, equation of motion of the particle is,
max=Fx
The gravitational force on mass m at distance r is,
F=GMmrR3 (towards O)
Therefore, Fx=−Fsinθ
=−GMmrR3(xr)
=−GMmR3.x
Since, Fx∝−x, motion is simple harmonic in nature. Further,
max=−GMmR3.x
or ax=−GMR3.x
∴ Time period of oscillstion is, T=2π√∣∣∣xax∣∣∣
=2π√R3GM
The time taken by particle to go from one end to the other is T2.
∴t=T2
=π√R3GM
 .
.
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Assertion And Reason
10 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Level 1 Single Correct
24 Videos
- SIMPLE HARMONIC MOTIONBOOK - DC PANDEYCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example Type 13
3 Videos
- SEMICONDUCTORS AND ELECTRONIC DEVICESBOOK - DC PANDEYCHAPTER - SEMICONDUCTORS AND ELECTRONIC DEVICESEXERCISE - More than One Option is Correct
3 Videos
- SOLVD PAPERS 2017 NEET, AIIMS & JIPMERBOOK - DC PANDEYCHAPTER - SOLVD PAPERS 2017 NEET, AIIMS & JIPMEREXERCISE - Solved paper 2018(JIPMER)
38 Videos
Similar Questions
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass (m) move in a circle of radius (r ) under the action of their mutual gravitational attraction. Find the speed of each particle.
View Solution
Knowledge Check
Four particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
AGmRB√2√2GMRC√GMR(2√2+1)D√GMR2√2+14Two particles of same mass m go around a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is ,
AV=12R√1GmBV=√GM2RCV=12√GmRDV=√4GmRFour particles each of mass M move along a circle of radius R under the action of their mutula gravitational attraction the speed of each paritcles is
A√GMRB√2√2GMRC√GMR(1+2√2)D12√GMR(1+2√2)
Two particles each of equal mass (m) move along a circle of radius (r) under the action of their mutual dravitational. Find the speed of each particle.

View SolutionFour particles each of mass M, move along a circle of radius R under the action of their mutual gravitational attraction as shown in figure. The speed of each particle is :
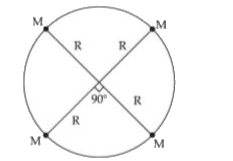
View SolutionTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
View SolutionImagine a narrow tunnel between the two diametrically opposite points of the earth. A particle of mass m is released in this tunnel . The time period of oscillation is
View SolutionTwo particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
View Solution
