Two particles move parallel to $x -$ axis about the origin with same amplitude 'a' and frequency $ω$ . At a certain instant they are found at a distance $a / 3$ from the origin on opposite sides but their velocities are in the same direction. What is the phase difference between the two?

${cos}^{- 1} (\frac{7}{9})$

${cos}^{- 1} (\frac{5}{9})$

${cos}^{- 1} (\frac{4}{9})$

${cos}^{- 1} (\frac{1}{9})$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

Two particles executes S.H.M. of the same amplitude and frequency along the same straight line. They pass one another when going in opposite directions, each time their displacement is root three by two times amplitude. The phase difference between them is
A $\frac{2 π}{3}$ rad
B $\frac{π}{2}$ rad
C $\frac{π}{6}$ rad
D $\frac{π}{3}$ rad
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
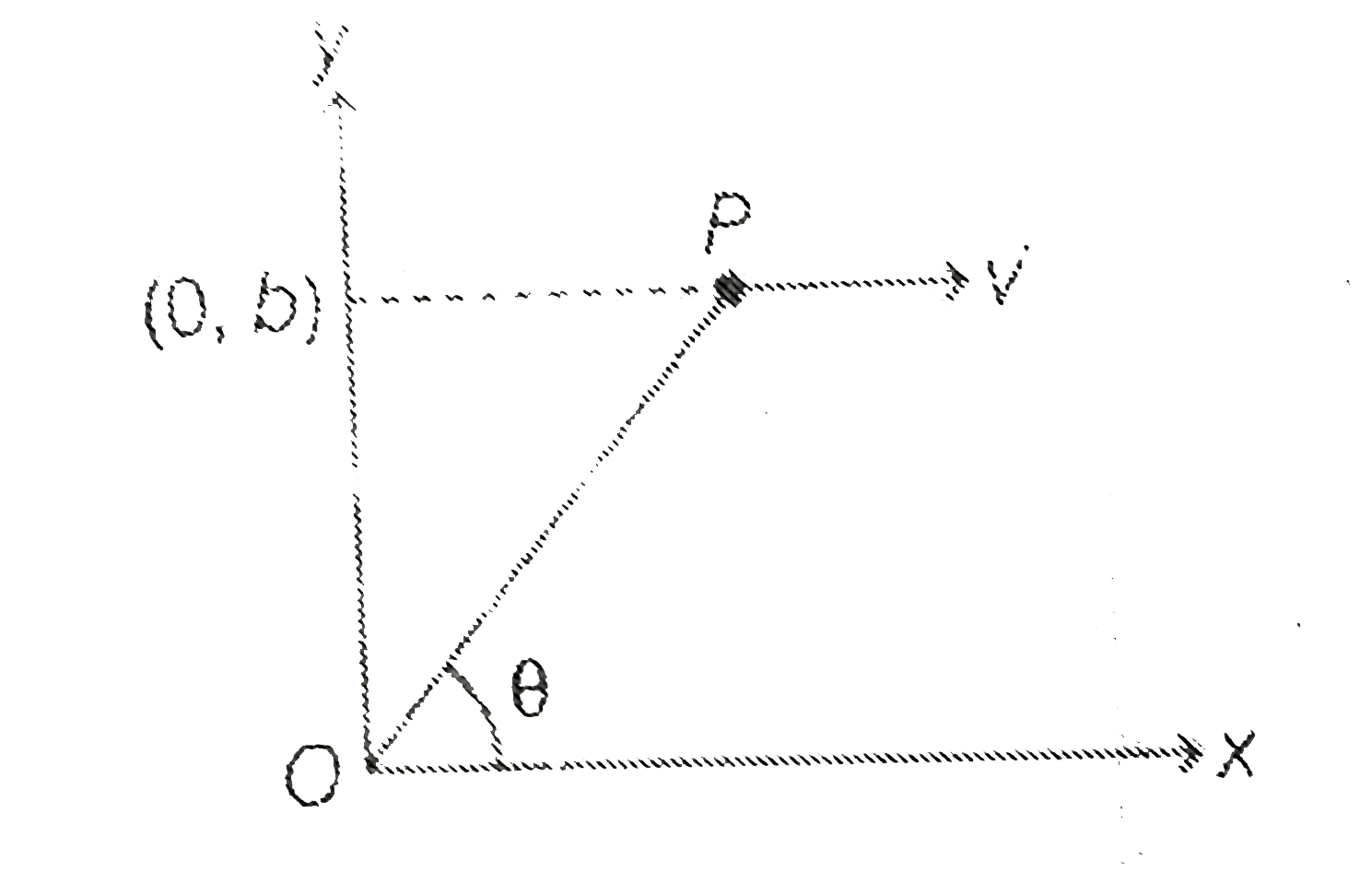A $(v / b) {sin}^{2} θ$
B $(v / b)$
C $(v / b) sin θ$
D $\frac{v}{b sin θ}$
Two particle are in $S H M$ on same striaght line with amplitude $A$ and $2 A$ and with same angular frequency $ω$ . It is observed that when first particle is at as distance $\frac{A}{\sqrt{2}}$ from origin and going toward mean position, other particle is at extreme postion on other side of mean positon. find phase difference betwenen he two paricles.
A $45^{\circ}$
B $90^{\circ}$
C $135^{\circ}$
D $180^{\circ}$