A wheel of radius R, mass m and moment of inertia I is pulled along a horizontal surface by application of force F to as rope unwinding from the axel of radius, r as shown in figure. Friction is sufficient for pure rolling of the wheel.
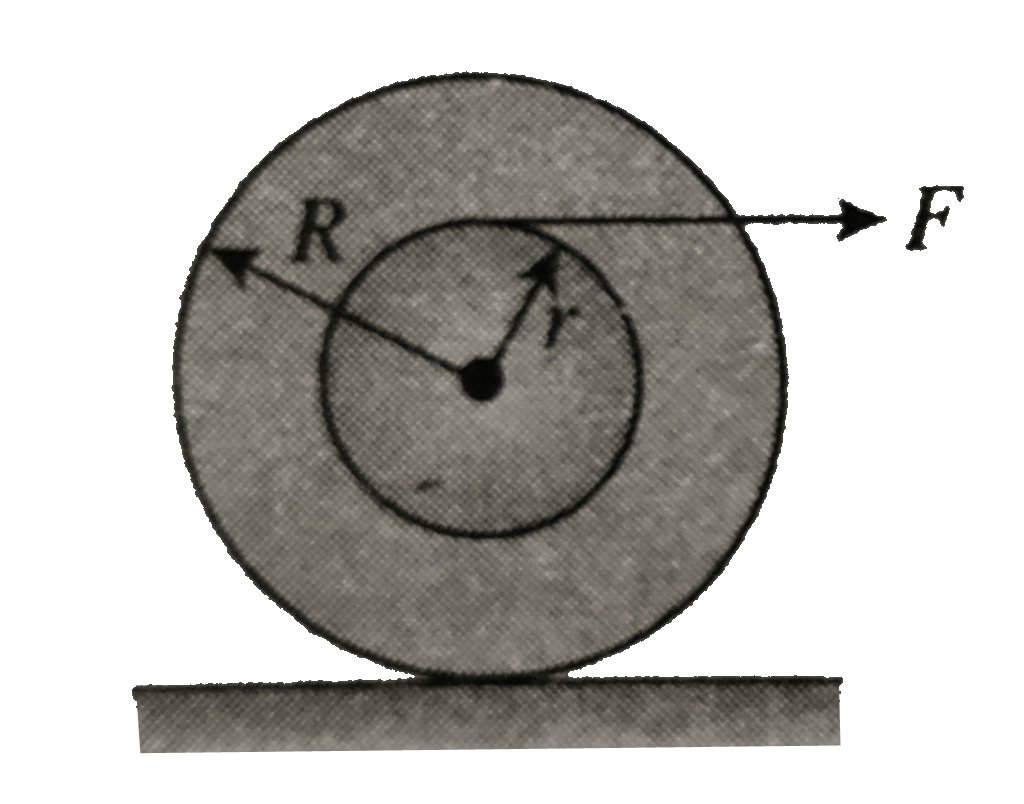
a. What is the linear acceleration of the wheel?
b. Calculate the frictional force that acts on the wheel.
The equations of the motion of the wheel are
F=f=ma……….i
F×r+f×R=Iα…….ii
in case of pure rolling a=Rα………iii

F×r+(F−ma)R=IRa
or a=F(r+R)R(I+mR2)
We can find acceleration of centre of wheel by another approach also. The point of contact will be instantaneous centre of rotation (ICR), and we apply torque equation about ICR.
F(R+r)=(I+mR2)α⇒α=F(R+r)(I+mR2)
Acceleration of centre of mass a=αR=F(R+r)R(I+mR2)
and the frictional force is
f=F−ma=F⎡⎢
⎢⎣1−(r+R)R(Im+R2)⎤⎥
⎥⎦=F[(Im)−Rr][(Im)+R2]
For Im=Rr Frictional force is zero.
For Im>Rr, frictional force positive i.e, it acts in backward direction.
For Im<Rr, frictional force is negative, i.e. it acts in forward direction.
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Solved Examples
12 Videos
- RIGID BODY DYNAMICS 2BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Exercise 3.1
11 Videos
- RIGID BODY DYNAMICS 1BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer
11 Videos
- SOUND WAVES AND DOPPLER EFFECTBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer
16 Videos
Similar Questions
A force F is applied at the top of a ring of mass M and radius R placed on a rough horizontal surface as shown in figure. Friction is sufficient to prevent slipping. The friction force acting on the ring is:

View SolutionA wheel of radius 20 cm is pushed ot move it on a rough horizontal surface. It is found to move through a distance of 60 cm on the road during the time it completes one revolutionabout the centre. Assume that the linear and the angular accelerations are uniform. The frictional force acting on the wheel by the surface is
View SolutionA disc of radius R and mass M is under pure rolling under the action of a force F applied at the topmost point as shown in figure. There is sufficient friciton between the disc and the horizontal surface. The acceleration is given as

View SolutionA hollow sphere of mass 'm' and radius 'R' are placed on horizontal surface and a horizontal force 'F' starts acting at a distance 'x' from its top most as shown in the figure.The value of 'x' such that hollow sphere starts pure rolling without use of friction is
_PHY_E05_157_Q01.png)
View SolutionA block of mass M is pulled along a horizontal frictionless surface by a rope of mass m as shown in A horizontal force F is applied to one end of the rope. Find
(a) the acceleration of the rope and block
(b) the force that the rope exerts on the block
(c) the tension in the rope at its mid point

View SolutionA constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?
View SolutionA wheel of radius 10 cm can rotate freely about its centre as shown in figure. A string is wrapped over its rim and is pulled by a force of 5.0 N. It is found that the torque produces an angular acceleration 2.0 rads−2 in the wheel. Calculate the moment of inertia of the wheel.

View SolutionA ring of mass m and radius R rolls on a horizontal roudh surface without slipping due to an applied force 'F'. The frcition force acting on ring is :−

View SolutionA wheel of radius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shown in figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. Initially, the wheel is rotating at a speed ω in direction such that the block slides up the plane. How far will the block move before stopping?
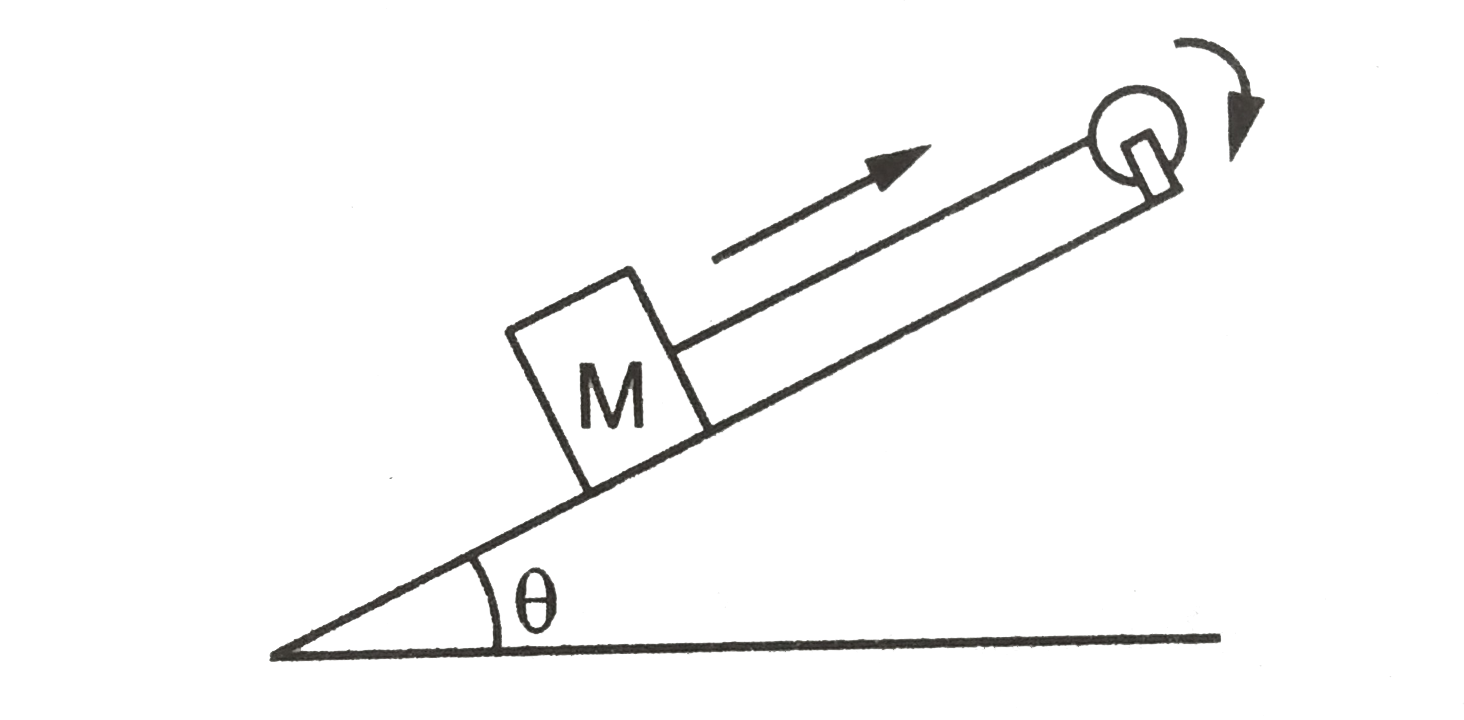
View Solution
A body of mass m, radius R and moment of inertia I (about an axis passing through the centre of mass and perpendicular to plane of motion) is released from rest over a sufficiently rough ground (to provide accelerated pure rolling) find linear acceleration of the body.
View Solution
