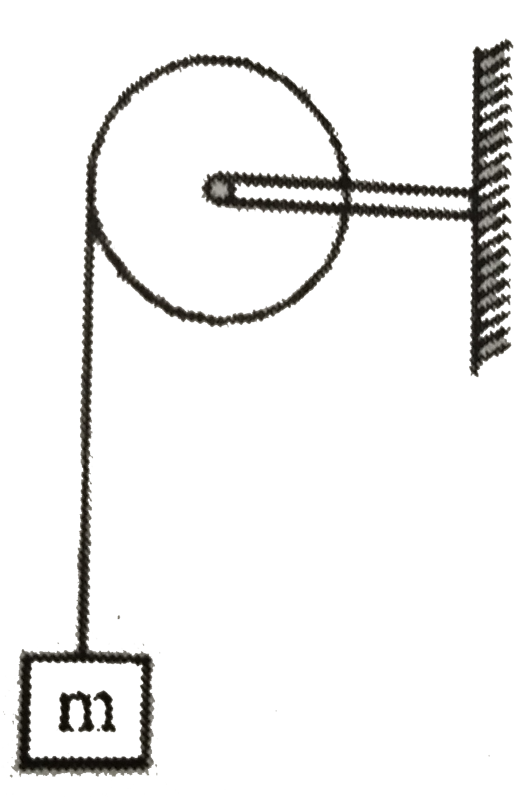
A wheel of radius r and moment of inertia I about its axis is fixed at top of an inclined plane of inclination θ as shown in figure. A string is wrapped round the wheel and its free end supports a block of mass M which can slide on the plane. Initially, the wheel is rotating at a speed ω in direction such that the block slides up the plane. How far will the block move before stopping?
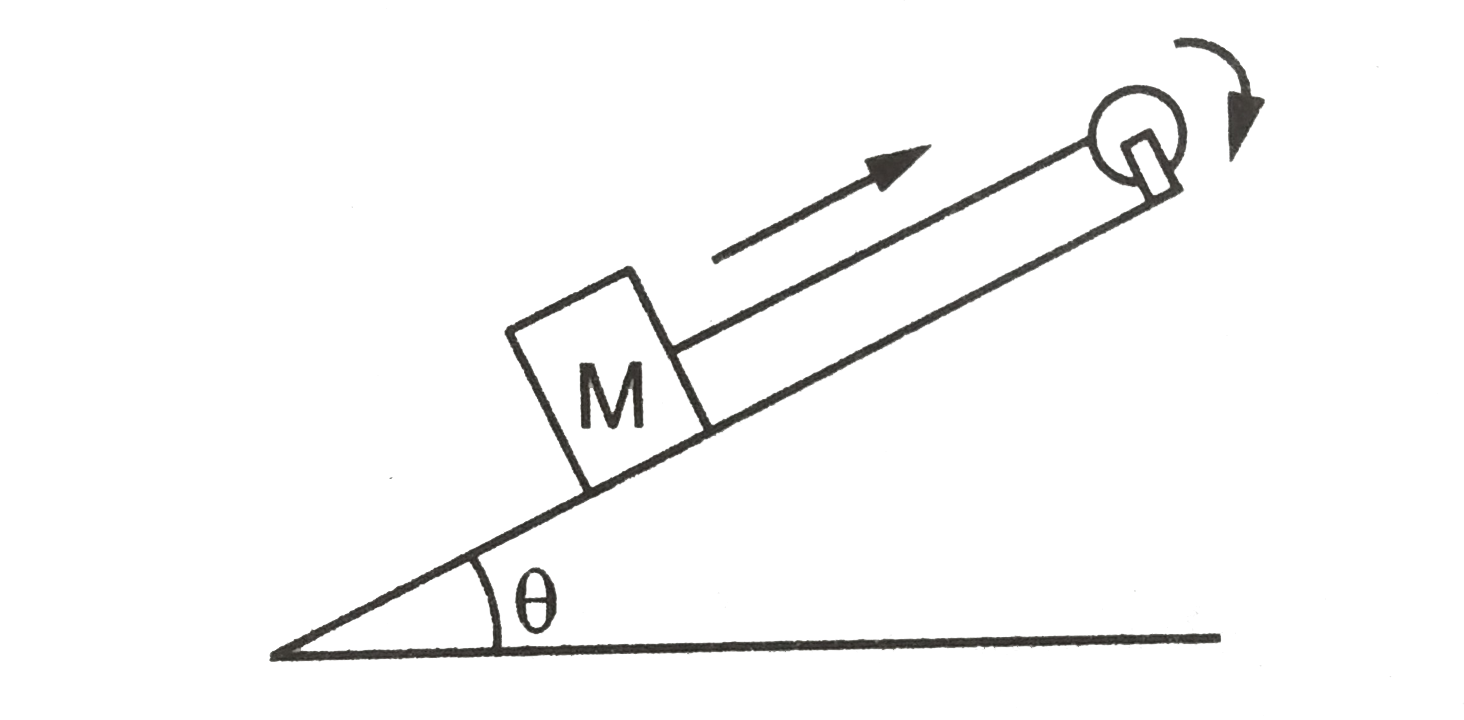
Suppose the deceleration of the block is a. The linear decelerationof the rim of the wheel is also a. The angular decelratinof the wheel is α=ar. I the tension in the string is T, the equations of motion are as follows:
Mgsinθ−T=Ma
and Tr=Iα=Iar
ElimiN/Ating T from these equations
Mgsinθ−Iar2=Ma
giving a=Mgr2sinθI+Mr2
THe initial velocity of the block up the incline is v=omegar.Thusthedistancemovedbytheblockbefores⊤πngis<br>x=v^2/(2a) =(omega^2r^2(I+Mr^2))/(2Mgr^2sintheta)=((I+Mr^2)omega^2)/(2Mgsintheta)
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A wheel of moment of inertia I and radius r is free to rotate about its centre as shown in figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. Find the speed of the block as it descends through a height h.
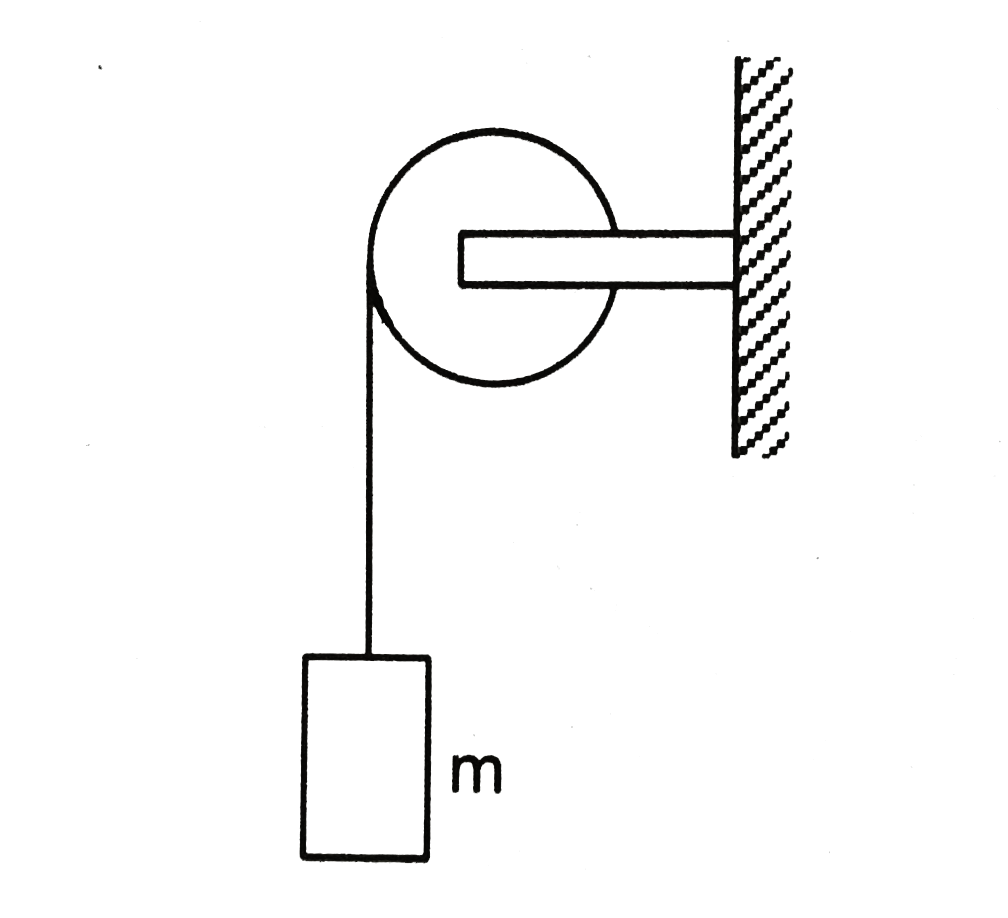
View SolutionA horizontal force F is applied to a block of mass m on a smooth fixed inclined plane of inclination θ to the horizontal as shown in the figure. Resultant force on the block up the plane is:

View SolutionA wheel having moment of inertia 2 kg m^2 about its axis, rotates at 50 rpm about this axis. Find the torque that can stop the wheel in one minute.
View SolutionA block of mass m moves with constant speed down the inclined plane of inclination θ. Find the coefficient of kinetic friction.
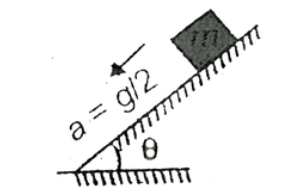
View SolutionA block of mass m slides down a rough inclined plane with an acceleration g2
View SolutionA wheel of mass M and radius a and M.I. IG (about centre of mass) is set rolling with angular velocity ω up a rough inclined plane of inclination theta. The distance traveled by it up the plane is
View SolutionA block of mass m slides down an inclined plane of inclination θ with uniform speed. The coefficient of friction between the block and the plane is μ. The contact force between the block and the plane is
View SolutionA disc of mass m and radius r is free to rotate about its centre as shown in the figure. A string is wrapped over its rim and a block of mass m is attached to the free end of the string. The system is released from rest. The speed of the block as it descends through a height h, is :-
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View SolutionA block of mass m is placed on a smooth inclined plane of inclination θ with the horizontal. The force exerted by the plane on the block has a magnitude
View Solution
