A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
To solve the problem step by step, we will analyze the collision between the particle and the rod using the principles of conservation of linear momentum and conservation of angular momentum.
Step 1: Analyze the initial conditions
- The particle of mass m is moving with a velocity v perpendicular to the rod.
- The rod of mass M is stationary on a smooth horizontal plane.
- The collision occurs at a distance a4 from the center of the rod.
Step 2: Apply conservation of linear momentum
Since there are no external forces acting on the system, the linear momentum before and after the collision must be conserved.
Initial momentum:
- The initial momentum of the system is due to the moving particle:
pinitial=mv+0=mv
Final momentum:
- After the collision, the particle stops, and the rod starts moving with a velocity V:
pfinal=MV
Setting initial momentum equal to final momentum:
mv=MV
From this, we can solve for V:
V=mvM
Step 3: Apply conservation of angular momentum
Next, we consider the angular momentum about the center of the rod. Since there are no external torques acting on the system, the angular momentum before and after the collision must also be conserved.
Initial angular momentum:
- The initial angular momentum of the system about the center of the rod (point A) is given by:
Linitial=m⋅v⋅(a4)
Final angular momentum:
- The final angular momentum consists of the angular momentum of the rod about its center of mass and the angular momentum of the center of mass of the rod about point A:
Lfinal=Iω+MV⋅0
where I is the moment of inertia of the rod about its center, given by I=112Ma2, and ω is the angular velocity of the rod.
Setting initial angular momentum equal to final angular momentum:
m⋅v⋅(a4)=112Ma2⋅ω
Step 4: Solve for angular velocity ω
Rearranging the equation to solve for ω:
ω=12mva4Ma2=3mvMa
Final Answers
1. The velocity of the center of the rod after the collision is:
V=mvM
2. The angular velocity of the rod about its center just after the collision is:
ω=3mvMa
- The particle of mass m is moving with a velocity v perpendicular to the rod.
- The rod of mass M is stationary on a smooth horizontal plane.
- The collision occurs at a distance a4 from the center of the rod.
Since there are no external forces acting on the system, the linear momentum before and after the collision must be conserved.
- The initial momentum of the system is due to the moving particle:
pinitial=mv+0=mv
Final momentum:
- After the collision, the particle stops, and the rod starts moving with a velocity V:
pfinal=MV
mv=MV
V=mvM
Next, we consider the angular momentum about the center of the rod. Since there are no external torques acting on the system, the angular momentum before and after the collision must also be conserved.
- The initial angular momentum of the system about the center of the rod (point A) is given by:
Linitial=m⋅v⋅(a4)
- The final angular momentum consists of the angular momentum of the rod about its center of mass and the angular momentum of the center of mass of the rod about point A:
Lfinal=Iω+MV⋅0
where I is the moment of inertia of the rod about its center, given by I=112Ma2, and ω is the angular velocity of the rod.
m⋅v⋅(a4)=112Ma2⋅ω
Rearranging the equation to solve for ω:
ω=12mva4Ma2=3mvMa
1. The velocity of the center of the rod after the collision is:
V=mvM
2. The angular velocity of the rod about its center just after the collision is:
ω=3mvMa
Topper's Solved these Questions
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -1
26 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Objective -2
14 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMA ENGLISHCHAPTER - ROTATIONAL MECHANICSEXERCISE - Questions for short Answer
21 Videos
- REST AND MOTION : KINEMATICSBOOK - HC VERMA ENGLISHCHAPTER - REST AND MOTION : KINEMATICSEXERCISE - Question for short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMA ENGLISHCHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Question for short Answer
15 Videos
Similar Questions
A uniform rod of mass 2kg and length 1m lies on a smooth horizontal plane. A particle of mass 1 kg moving at a speed of 2ms−1 perpendicular to the length of the rod strikes it at a distance 14 m from the centre and stops . Find the angular velocity of the rod about its centre just after the collision (in rad/s)
View SolutionA uniform rod of length L lies on a smooth horizontal table. The rod has a mass M. A particle of mass m moving with speed v strikes the rod perpendicularly at one of the ends of the rod sticks to it after collision.
Find the velocity of the particle with respect to C before the collision
View SolutionA uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View Solution
A thin, uniform rod of mass M and length L is at rest on a smooth horizontal surface. A particle of same mass M collides with the rod at one end perpendicular to its length with velocity V∘ and sticks to it. C is the middle point of the rod and D is a point at a distance of L/4 from end A. the time taken by the rod turn through 90∘ after collisions.
View SolutionA rod of mass 4m and length L is hinged at the mid point. A ball of mass 'm' moving with speed V in the plane of rod, strikes at the end at an angle of 45∘ and sticks to it. The angular velocity of system after collision is-
View Solution
A uniform rod of mass 3 m and length l is lying on a smooth horizontal surface. Two particle of mass m and 2 m moving with speed 2v0 and v0 in the opposite directly hit the rod perpendicularly at a distance l3 and l6 from the midpoint O of the rod ad stick to it after collision. if the loss in kinetic energy of the system due to collision is n5mv20 find the value of n.
View SolutionA Iong slender rod of mass 2kg and length m is placed on a smooth horizontal table. Two particles of masses 2kg and 1kg strike the rod simultaneously and stick to the rod after collision as shown in fig.
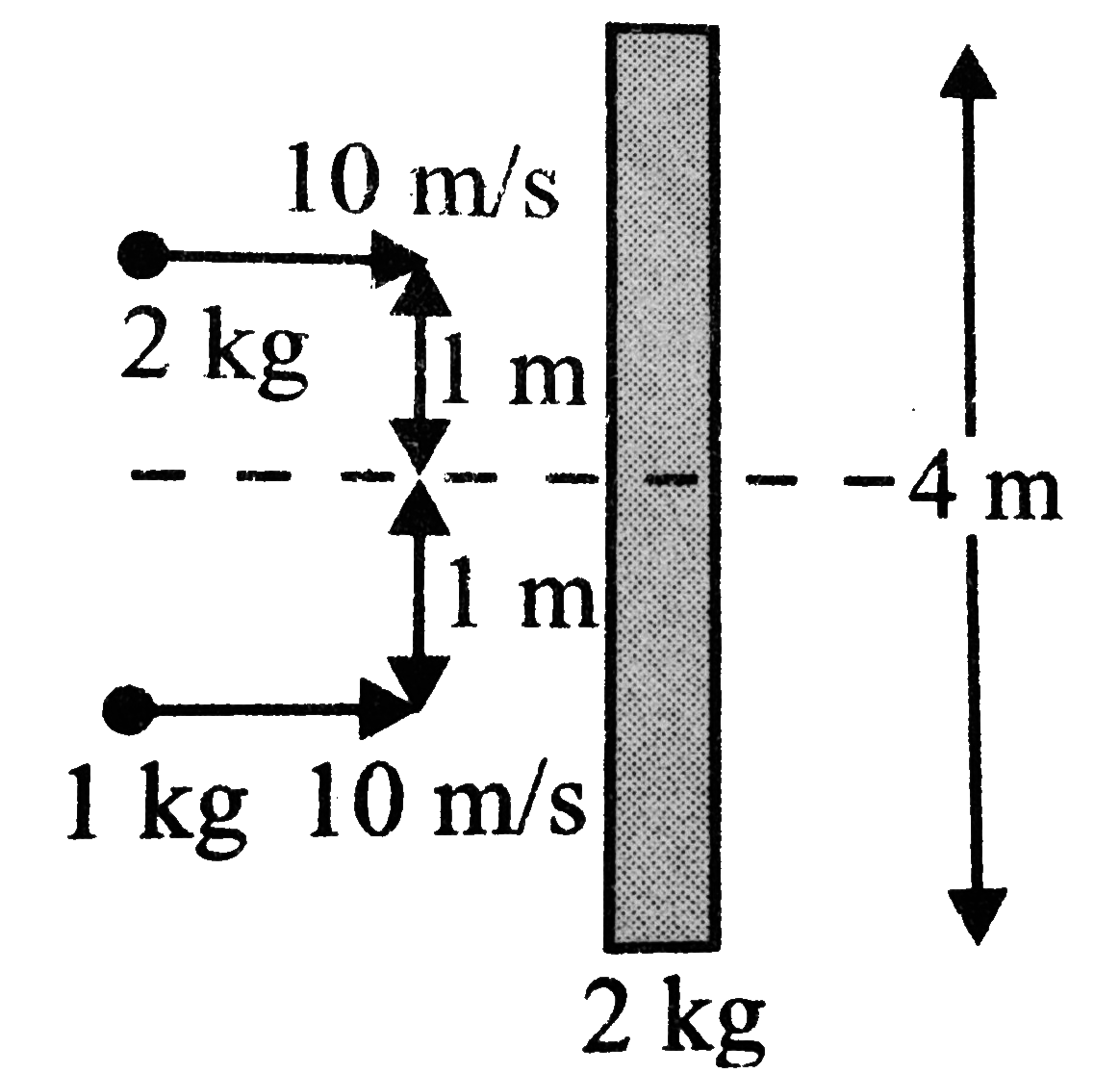
Velocity of the centre of mass of the rod after collision is
View SolutionA uniform rod of length 8 a and mass 6 m lies on a smooth horizontal surface. Two point masses m and 2 m moving in the same plane with speed 2 v and v respectively strike the rod perpendicular at distances a and 2a from the mid point of the rod in the opposite directions and stick to the rod. The angular velocity of the system immediately after the collision is
View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View Solution
