A sphere of mass and radius shown in figure slips on a rough horizontal plane. At some instant it has translational velocity and rotational velocity about the centre . Find the translational velocity after the sphere starts pure rolling.
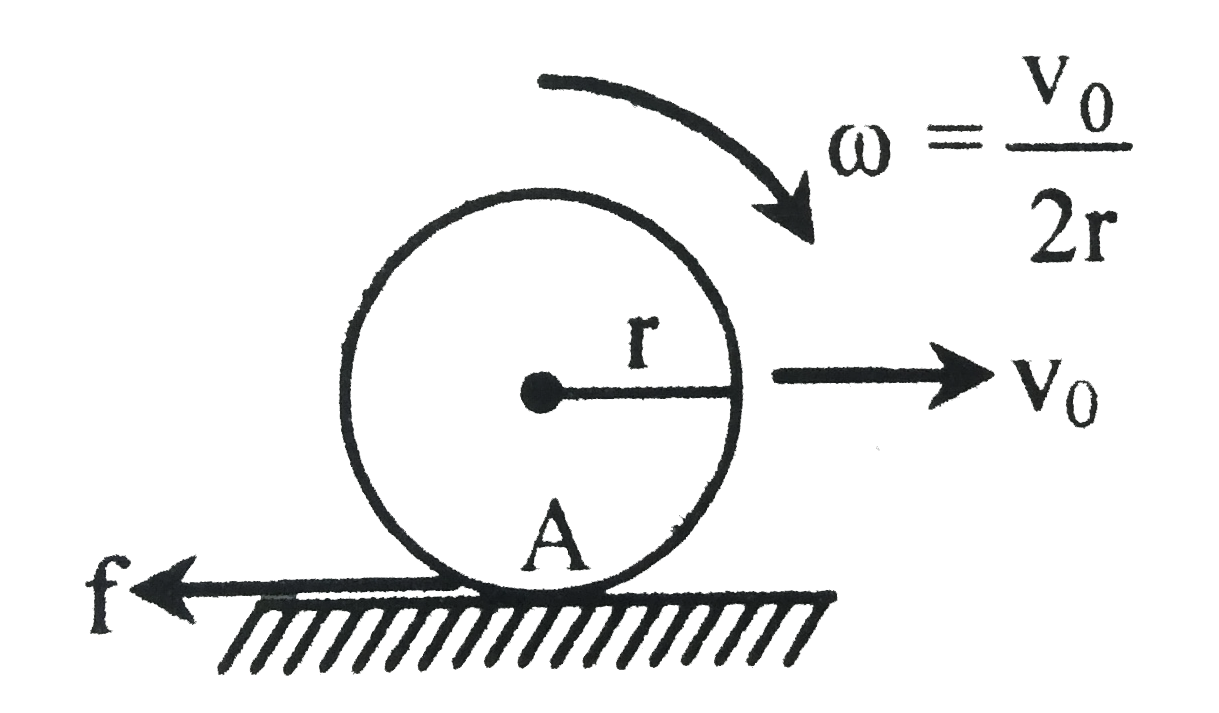 .
.
Velociyt of the centre and the angular velocity about the centre . Thus The sphre slips forward and thsu the friction by the plane on the sphere will act backward. As the friction is kinetic its value is and the sphere will be decelerated by Hence
............i
This friction will also have a torque about the centre. This torque is clockwise and in the directionof . Hence the angular acceleration about the centre will be
and the clockwise angular velocity at time t will be
pure rolling starts when v(t)=romega(t)v(t)=v_0/2+(5f)/(2M)t5/2v(t)+v(t) =5/2 v_0+v_0/2v(t)=2/7xx3v_=6/7v_06v_0/7L=L_(cm)+Mrv_0+I_(cm)omega+Mrv_)=(2/5Mr^2)(v_0)/(2r)+Mrv_0=6/5Mrv_0v/rL=L_(cm)+Mrv=(2/5Mr^2)(v/r)+mrv+7/5Mrv6/5Mrv_0=7/5Mrvor v=6/7v_0
Topper's Solved these Questions
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -1
Explore 26 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Objective -2
Explore 14 Videos
- ROTATIONAL MECHANICSBook:HC VERMA ENGLISHChapter:ROTATIONAL MECHANICSExercise:Questions for short Answer
Explore 21 Videos
- REST AND MOTION : KINEMATICSBook:HC VERMA ENGLISHChapter:REST AND MOTION : KINEMATICSExercise:Question for short Answer
Explore 13 Videos
- SIMPLE HARMONIC MOTIONBook:HC VERMA ENGLISHChapter:SIMPLE HARMONIC MOTIONExercise:Question for short Answer
Explore 15 Videos
Similar Questions
A sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v0, and rotational velocity about centre v0/2r. The percentage change of translational velocity after the sphere start pure rolling:

View SolutionA wheel is rolling on a horizontal plane. At a certain instant it has a velocity v and acceleration a of CM as shown in figure . Acceleration of
View SolutionA sphere of mass m and radius r is placed on a rough plank of mass M. The system is placed on a smooth horizontal surface. A constant force F is applied on the plank such that the sphere rolls purely on the plank. Find the acceleration of the sphere.

View SolutionA uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA uniform sphere of radius R is palced on a rough horizontal surface and given a linear velocity v0 and an angular velocity ω0 as shown . If the angular velocity and the linear velocity both become zero simultaneously, then
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionA ring of mass m and radius R is placed on a rough horizontal surface (co-efficient of friction μ) with velocity of C.M.v0 and angular speed 2V0R as shown in figure. Initially the ring is rolling with slipping but attains pure rolling motion after some time t. Then
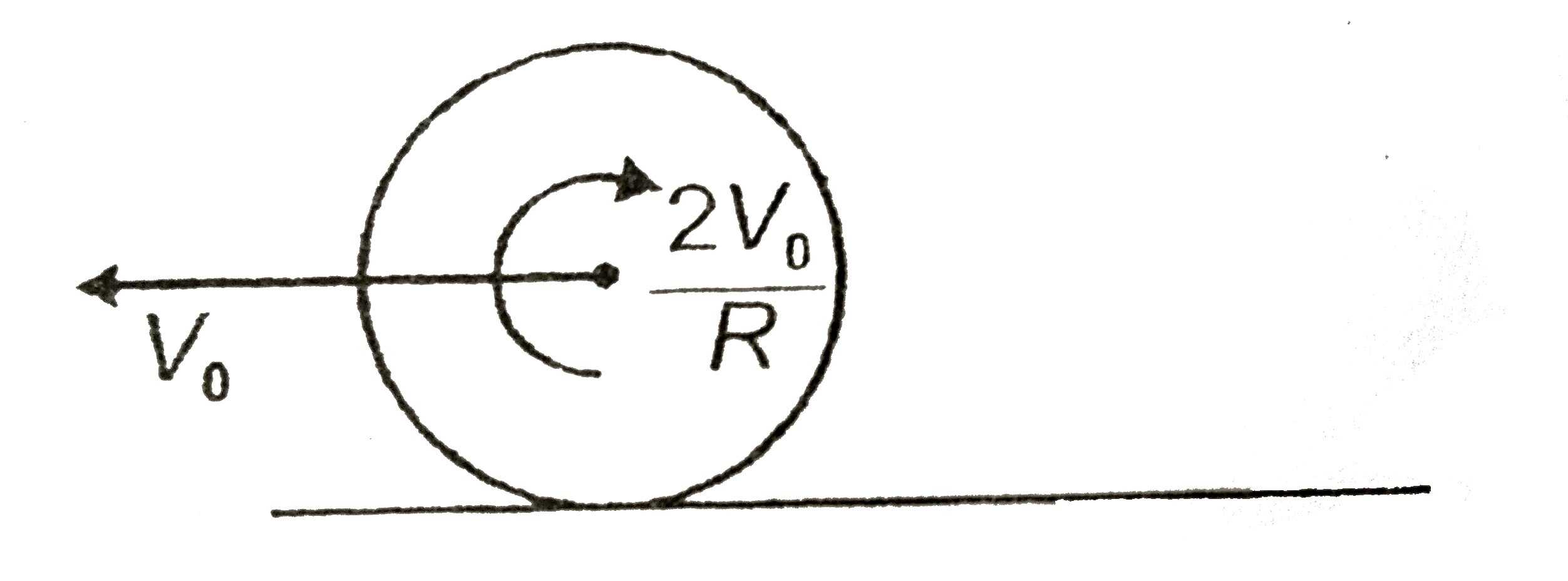
View SolutionA sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
View SolutionA sphere of mass M and radius R is moving on a rough fixed surface, having coefficient of friction μ. as shown in Fig. It will attain a minimum linear velocity after time (v0>ω0R)

View Solution

