A uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
a)3pml
b)pml
c)p2ml
d)2pml
The correct Answer is:A
To find the angular velocity of a uniform rod of mass m and length l after it is given a sharp horizontal impulse p at a distance l4 from its center, we can follow these steps:
1. Understanding the System:
- We have a uniform rod of mass m and length l resting on a smooth horizontal surface.
- An impulse p is applied perpendicular to the rod at a distance of l4 from the center.
2. Identify the Point of Application of Impulse:
- The impulse is applied at a distance l4 from the center of the rod. This means the distance from the center to the point of application is d=l4.
3. Calculate the Torque due to the Impulse:
- The torque (τ) caused by the impulse about the center of mass is given by:
\(
\tau = p \cdot d = p \cdot \frac{l}{4}
\)
4. Angular Impulse-Momentum Theorem:
- According to the angular impulse-momentum theorem, the change in angular momentum (ΔL) is equal to the torque multiplied by the time duration (Δt) of the impulse:
\(
\tau = \Delta L
\)
- Since the impulse is instantaneous, we can consider the angular momentum just after the impulse is applied.
5. Moment of Inertia of the Rod:
- The moment of inertia (I) of a uniform rod about its center is given by:
\(
I = \frac{1}{12} m l^2
\)
6. Relate Torque to Angular Velocity:
- The angular momentum (L) just after the impulse is:
\(
L = I \cdot \omega
\)
- Setting the torque equal to the change in angular momentum gives:
\(
p \cdot \frac{l}{4} = I \cdot \omega
\)
7. Substituting the Moment of Inertia:
- Substitute the expression for moment of inertia into the equation:
\(
p \cdot \frac{l}{4} = \frac{1}{12} m l^2 \cdot \omega
\)
8. Solving for Angular Velocity (ω):
- Rearranging the equation to solve for ω:
\(
\omega = \frac{p \cdot \frac{l}{4}}{\frac{1}{12} m l^2}
\)
- Simplifying this expression:
\(
\omega = \frac{p \cdot 12}{m l} \cdot \frac{1}{4} = \frac{3p}{ml}
\)
Final Result:
The angular velocity of the rod after the impulse is given by:
\(
\omega = \frac{3p}{ml}
\)
- We have a uniform rod of mass m and length l resting on a smooth horizontal surface.
- An impulse p is applied perpendicular to the rod at a distance of l4 from the center.
- The impulse is applied at a distance l4 from the center of the rod. This means the distance from the center to the point of application is d=l4.
- The torque (τ) caused by the impulse about the center of mass is given by:
\(
\tau = p \cdot d = p \cdot \frac{l}{4}
\)
- According to the angular impulse-momentum theorem, the change in angular momentum (ΔL) is equal to the torque multiplied by the time duration (Δt) of the impulse:
\(
\tau = \Delta L
\)
- Since the impulse is instantaneous, we can consider the angular momentum just after the impulse is applied.
- The moment of inertia (I) of a uniform rod about its center is given by:
\(
I = \frac{1}{12} m l^2
\)
- The angular momentum (L) just after the impulse is:
\(
L = I \cdot \omega
\)
- Setting the torque equal to the change in angular momentum gives:
\(
p \cdot \frac{l}{4} = I \cdot \omega
\)
- Substitute the expression for moment of inertia into the equation:
\(
p \cdot \frac{l}{4} = \frac{1}{12} m l^2 \cdot \omega
\)
- Rearranging the equation to solve for ω:
\(
\omega = \frac{p \cdot \frac{l}{4}}{\frac{1}{12} m l^2}
\)
- Simplifying this expression:
\(
\omega = \frac{p \cdot 12}{m l} \cdot \frac{1}{4} = \frac{3p}{ml}
\)
The angular velocity of the rod after the impulse is given by:
\(
\omega = \frac{3p}{ml}
\)
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Linked Comprehension
Explore 71 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 2Exercise:Subjective
Explore 19 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICS ENGLISHChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
A uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA uniform rod of mass m and length L is at rest on a smooth horizontal surface. A ball of mass m, moving with velocity v0, hits the rod perpendicularly at its one end and sticks to it. The angular velocity of rod after collision is

View SolutionA uniform rod of mass m and length l rests on a smooth horizontal surface. One of the ends of the rod is struck in a horizontal direction at right angles to the rod. As a result the rod obtains velocity v0. Find the force with which one-half of the rod will act ont he other in the process of motion.
View SolutionA uniform rod of mass m=2kg and length l is kept on a smooth horizontal plane. If the ends A and B of the rod move with speeds v and 2v respectively perpendicular to the rod, find the:
a. angulr velocity of CM of the rod.
b. Kinetic energy of the rod (in Joule).

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B, perpendicular to the rod in the horizontal direction. Speed of particlem P at a distance l6 from the centre towards A of the rod after time t=πml12J is.
View SolutionA uniform smooth rod (mass m and length l) placed on a smooth horizontal floor is it by a particle (mass m) moving on the floor, at a distance l4 from one end elastically (e=1). The distance travelled by the centre of the rod after the collision when it has completed three revolutions will be
View SolutionA conducting rod of mass m and length l is placed over a smooth horizontal surface. A uniform magnetic field B is acting perpendicular to the rod. Charge q is suddenly passed through the rod and it acquires an initial velocity v on the surface, then q is equal to
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
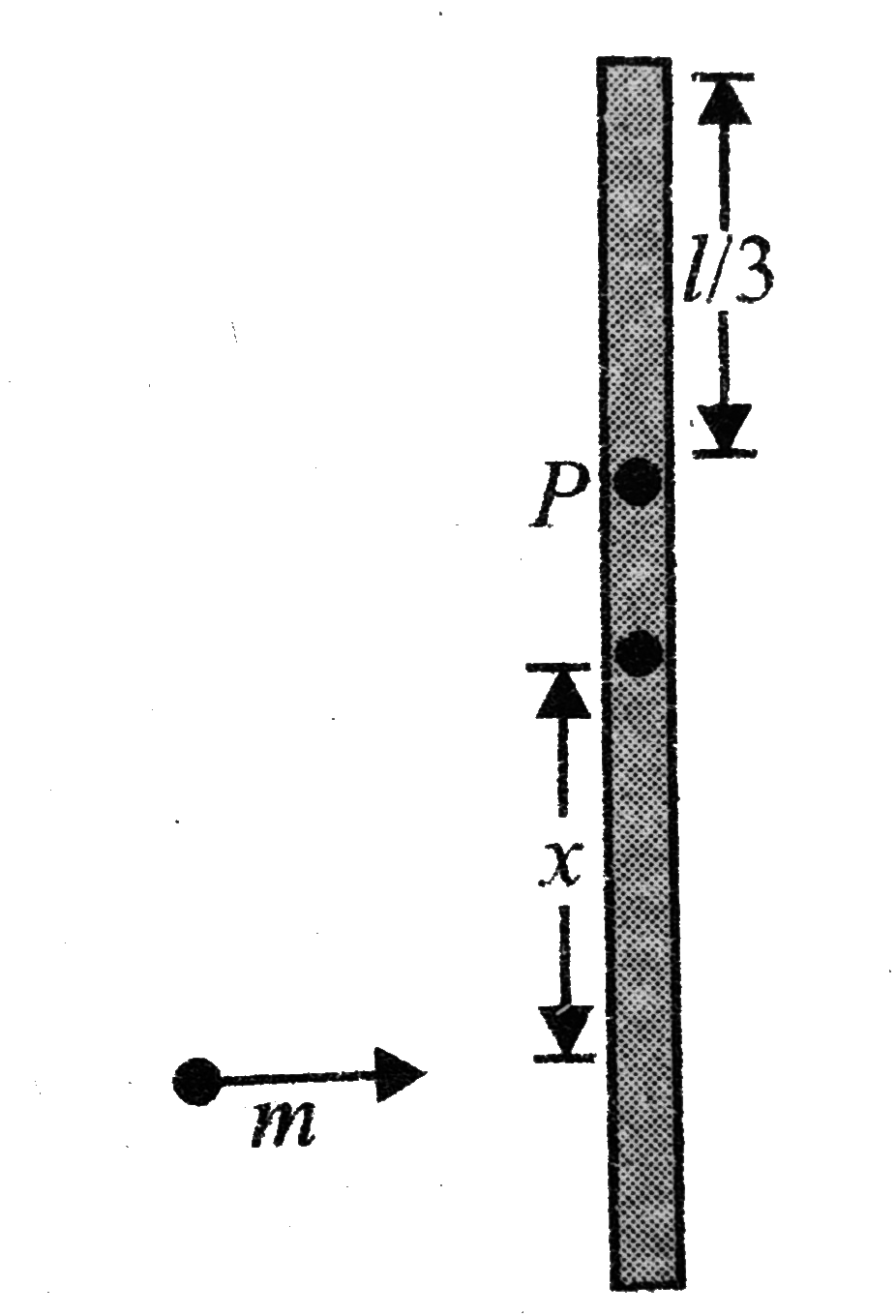
View Solution

