Calculate the force F that is applied horizontally at the axle of the wheel which is necessary to raise the wheel over the obstacle of height 0.4m. Radius of wheel is 1m and mass=10kg . F is

100N
66N
167N
133.3N
The correct Answer is:D
Taking moment of forces about point P , we get

F×0.6=100×0.8
or F=10×0.80.6=B=8006N=4003N=133.3N
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
The minimum horizontal force applied to the centre of wheel of radius R and weight w to pull it over a step of height R/2
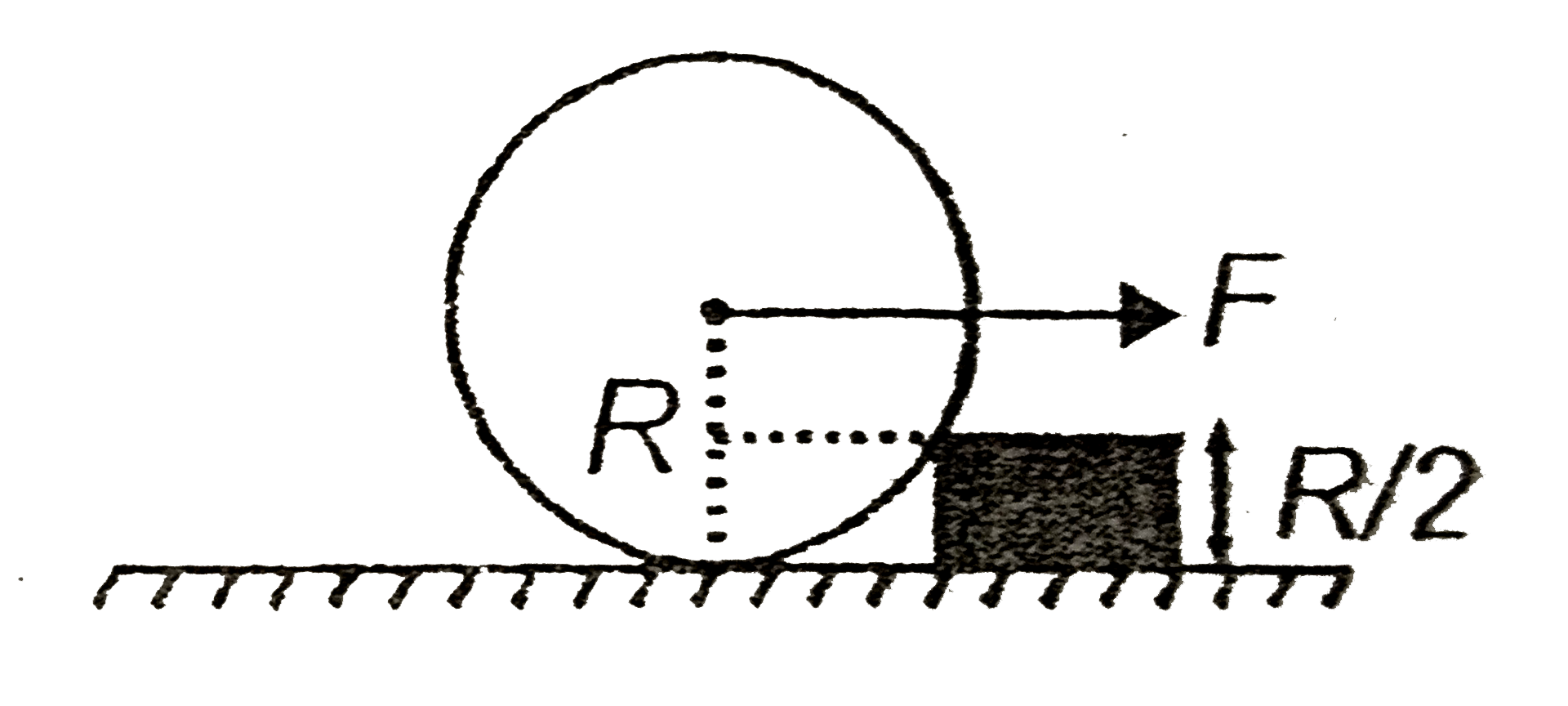 View Solution
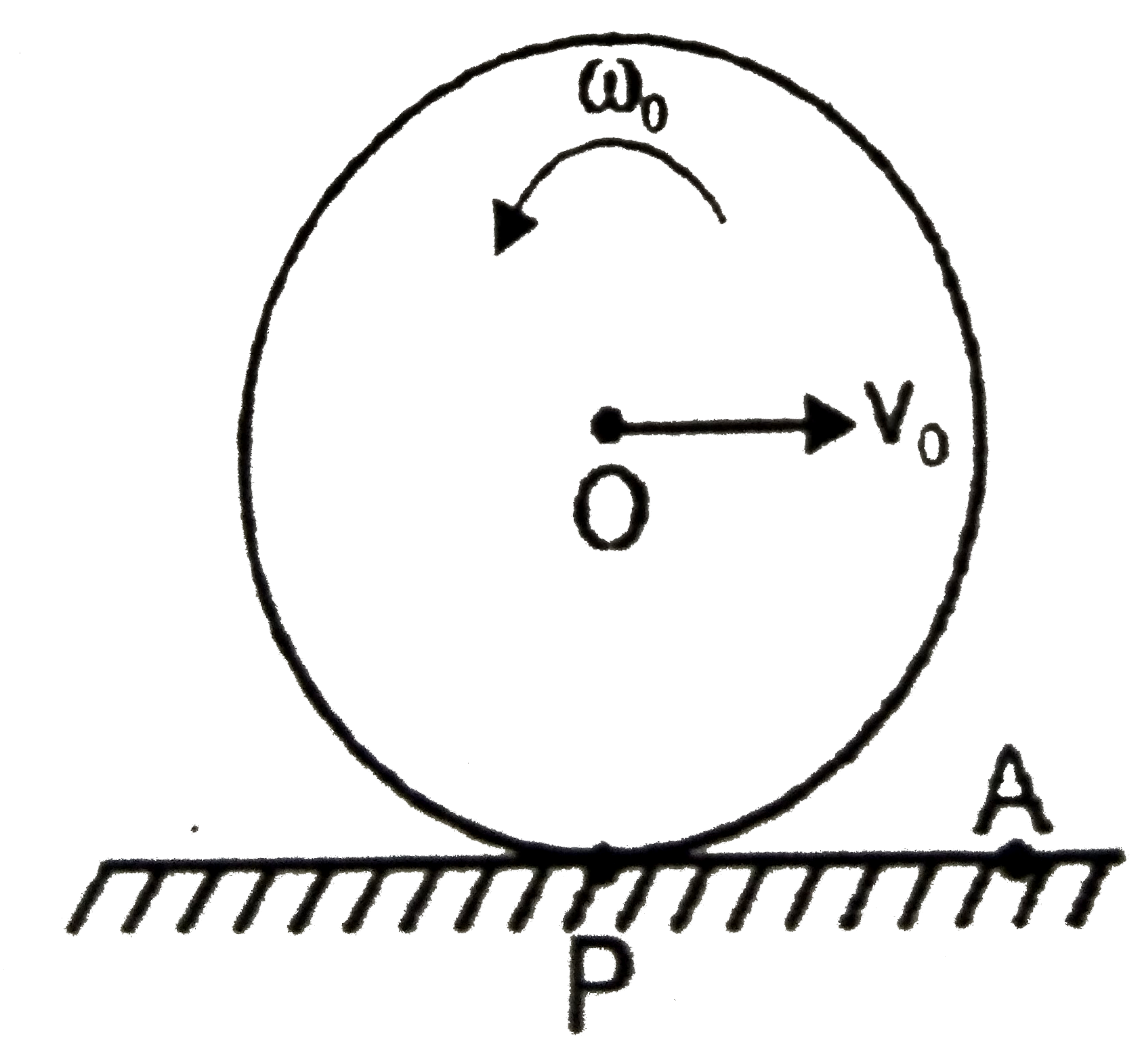
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
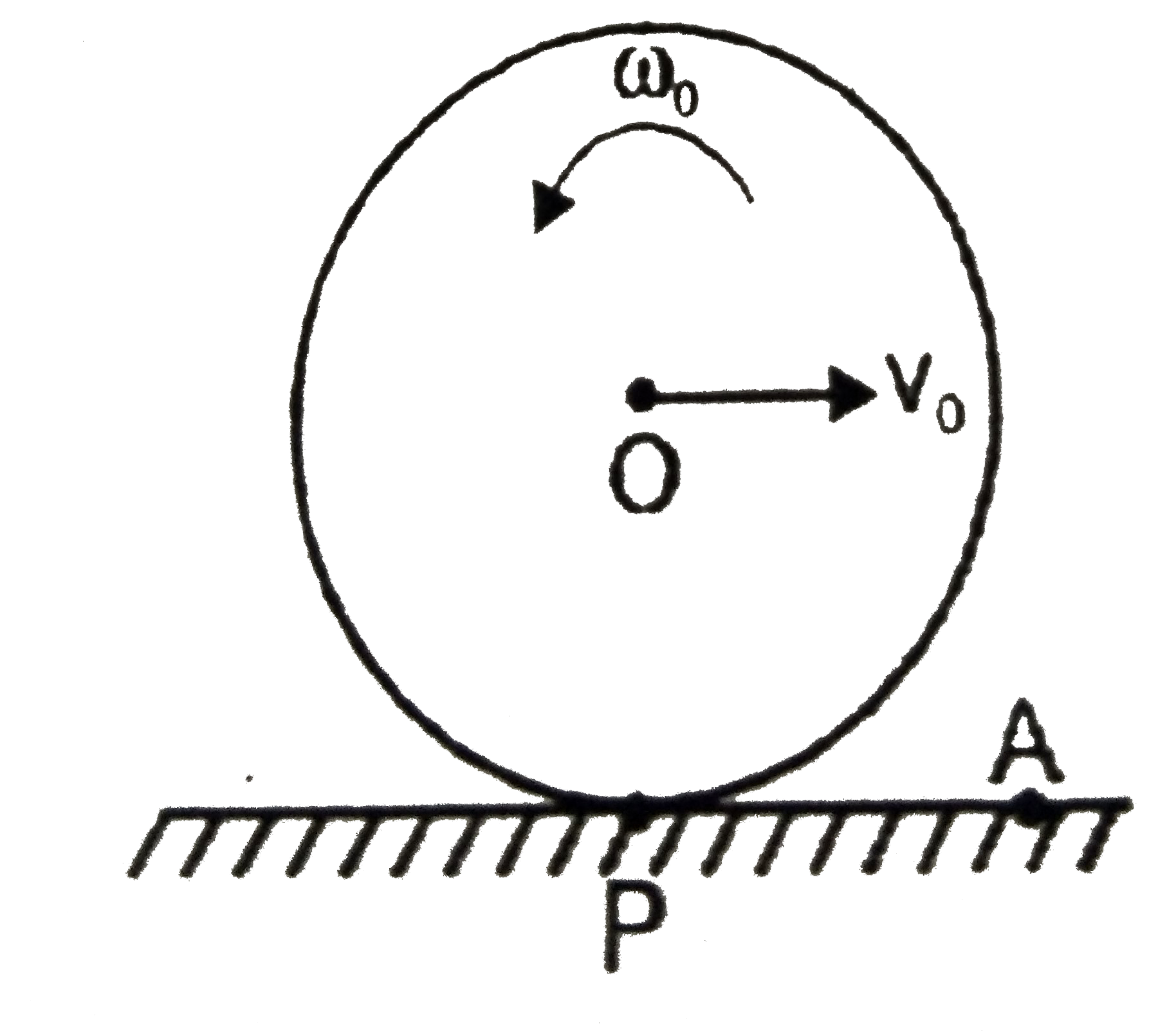
If above question , distance travelled by centre of mass of the wheel before it stops is −View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
If the wheel comes to permanent rest after sometimes, then :View SolutionA point in the rim of a wheel 4 m in diameter has linear velocity of 16ms−1 The angular velocity of wheel is
View SolutionThe drwing shows a bicycle wheel of radius r, resting against a small step whose height is h=r/5. A clockwise torque increases, there comes a time when the wheel just begins to rise up and loses contact with the ground. Let this torque be T. What is the magniitude of the horizontal component of the acceleration of the centre of the wheel when a torque of 2T is applied? Assume that the wheel doesn't slip at the edge of the step when this torque is applied (ignore the mass of the spokes).
 View Solution
View SolutionA wheel is released on a rough horizontal floor after imparting it an initial horizontal velocity v0 and angular velocityω0 as shown in the figure below. Point O is the centre of mass of the wheel and point P is its instantaneous point of contact with the groundl. The radius of wheel is r and its radius of gyration about O is k. Coefficient of friction between wheel and ground is μ. A is a fixed point on the ground.
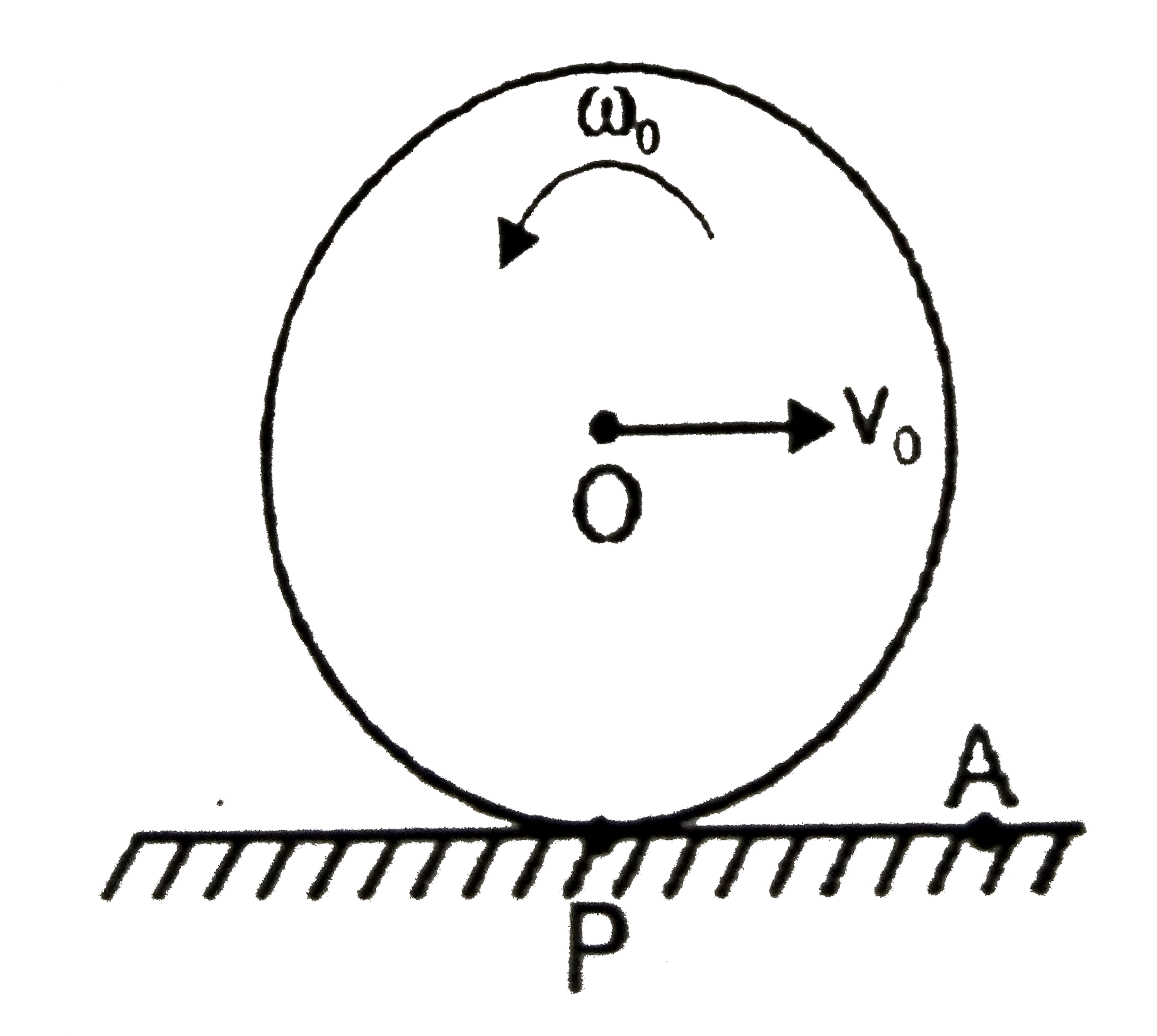
Which of the following is conserved ?View SolutionAt t=0, a force F=at2 is applied to a small body of mass m at an angle α resting on a smooth horizontal plane
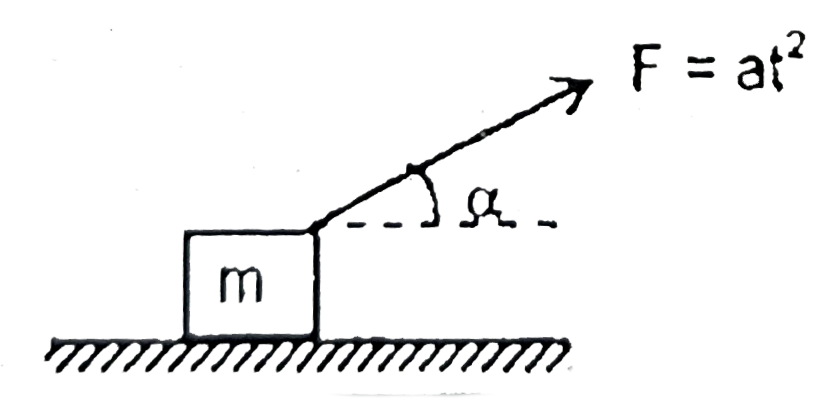 View Solution
View SolutionA constant horizontal force of 10N is applied at the centre of a wheel of mass 10kg and radius 0.30m. The wheel rolls without slipping on the horizontal surface, and the acceleration of the centre of mass is 0.60m/s2.
a. What are the magnitude and direction of the frictional force on the wheel?
b. What is the rotational inertia of the wheel about an axis through its centre of mass and perpendicular to the plane of the wheel?View SolutionA point P consider at contact point of a wheel on ground which rolls on ground without sliping then value of displacement of point P when wheel completes half of rotation (If radius of wheel is 1m) : -
View SolutionA wheel with 4 spokes is placed with its plane perpendicular to a uniform magnetic field B of magnitude 0.5 T. The field is directed into the plane of the paper and is present over the entire region of the wheel as shown in Fig. When the switch S is closed, there is initial current of 6 A between the axis and the rim and the wheel begins to rotate. Resistances of the spokes are 1, 2, 4 and 8 Ω, respectively. Resistance of rim is negligible.
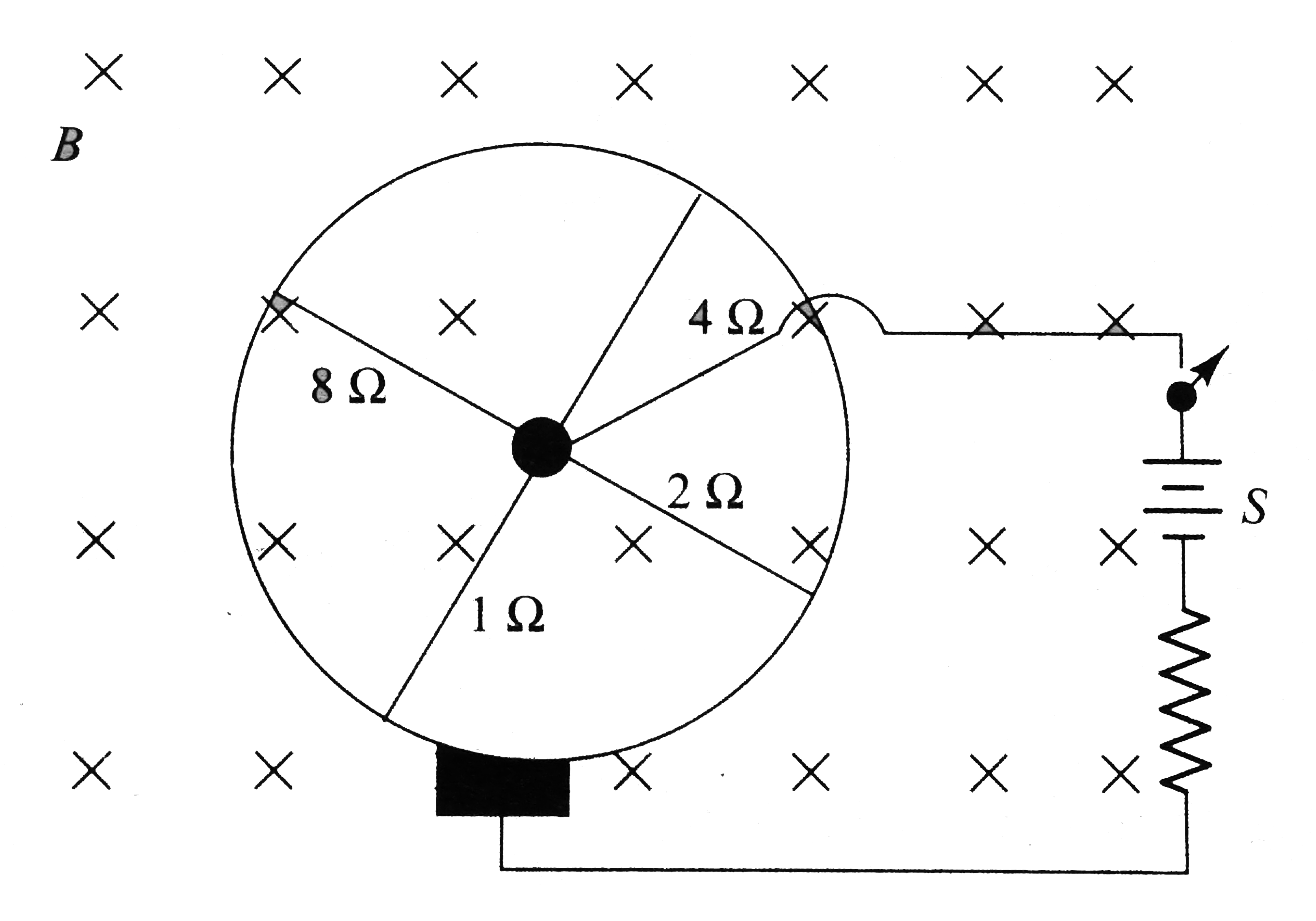
a. What is the direction of rotation of the wheel?
b. Radius of the wheel is 0.2 m. Calculate initial torque acting on the wheel.View Solution
