A point in the rim of a wheel 4 m in diameter has linear velocity of 16ms−1 The angular velocity of wheel is
4rads−1
8rads−1
12sin40∘
20rads−1
The correct Answer is:B
To find the angular velocity of the wheel, we can follow these steps:
Step 1: Identify the diameter and calculate the radius
The diameter of the wheel is given as 4 meters. The radius (R) is half of the diameter.
R=Diameter2=4m2=2m
Step 2: Use the formula for linear velocity
The relationship between linear velocity (V) and angular velocity (ω) is given by the formula:
V=ω×R
Where:
- V is the linear velocity,
- ω is the angular velocity,
- R is the radius.
Step 3: Rearrange the formula to solve for angular velocity
We can rearrange the formula to find angular velocity (ω):
ω=VR
Step 4: Substitute the known values
We know the linear velocity V=16m/s and the radius R=2m. Substituting these values into the equation gives:
ω=16m/s2m=8rad/s
Step 5: Conclusion
The angular velocity of the wheel is 8rad/s.
---
The diameter of the wheel is given as 4 meters. The radius (R) is half of the diameter.
The relationship between linear velocity (V) and angular velocity (ω) is given by the formula:
- V is the linear velocity,
- ω is the angular velocity,
- R is the radius.
We can rearrange the formula to find angular velocity (ω):
We know the linear velocity V=16m/s and the radius R=2m. Substituting these values into the equation gives:
The angular velocity of the wheel is 8rad/s.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
A point on the rim of a wheel 3 m in diameter has linear velocity of 18 ms−1 . The angular velocity of the wheel is
View SolutionA particle moves in a circle of radius 4 m with a linear velocity of 20ms−1. Find the angular velocity.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA particle is moving along a circle of radius 20cm, with a linear velocity of 2m//s. Calculate the angular velocity of the particle.
View SolutionA fly wheel is rotating about its own axis at an angular velocity 11rads−1, its angular velocity in revolution per minute is
View SolutionIn an undershot water wheel, the cross-sectional ara a=0.1m2 of the stream is striking the series of radial flat vanes of the wheel. The velocity of stream is 6m/s. The velocity of vanes is 3m/s. If the power supplied by jet (in watts) is 2700K find K.

View SolutionA string is wrapped around the rim of a wheel of moment of inertia 0.20 kg-m^2 and radius 20 cm. The wheel is free to rotate about it axis. Initially, the wheel is at rest. The string is now pulled by a force of 20 N. Find the angular velocity of the wheel after 5.0 seconds.
View SolutionA cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and MI is I. A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
View SolutionA wheel rolls purely on ground. Find a point on the periphery of a body which has a velocity equal in magnitude to the velocity of the centre of mass of the body.
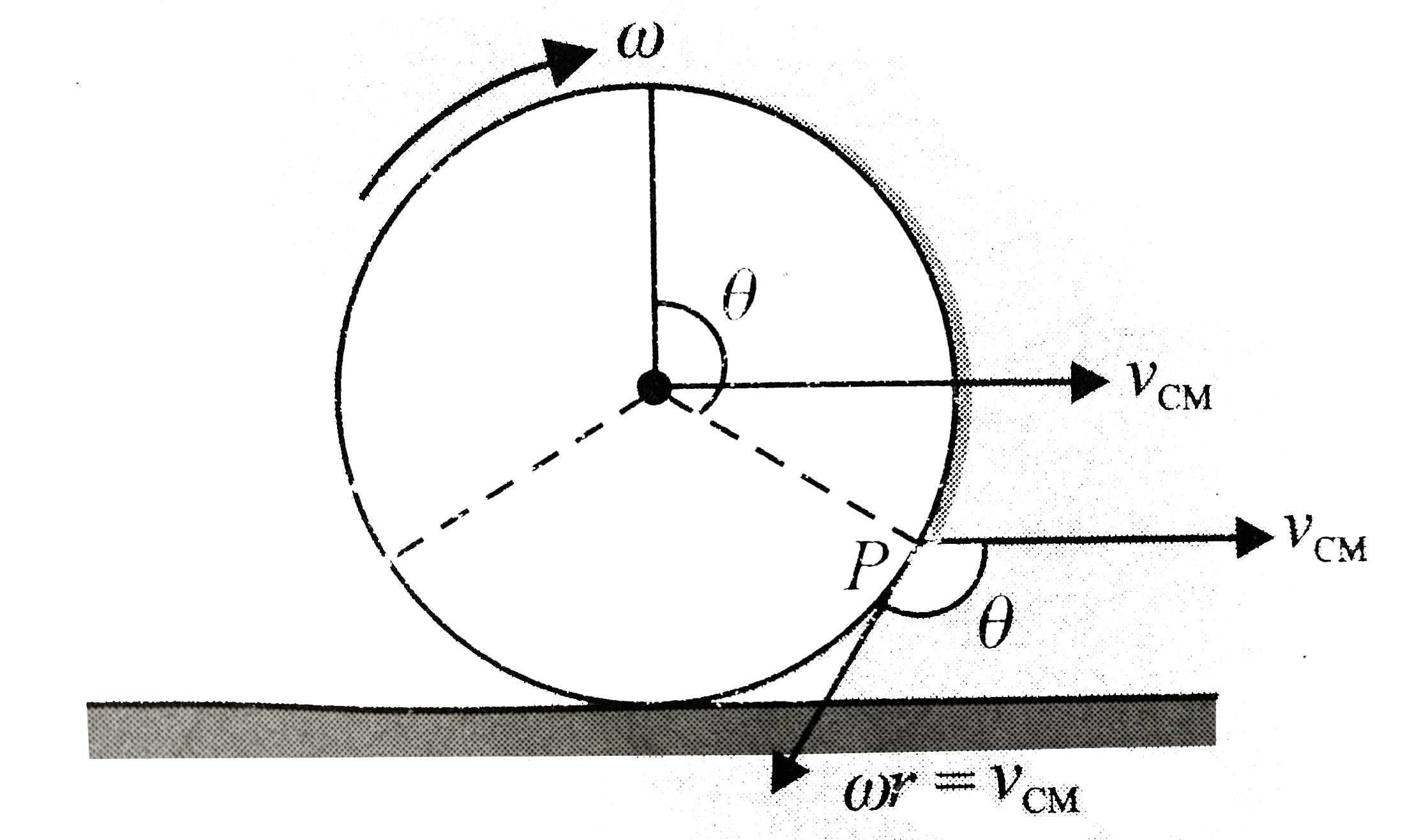
View SolutionA particle is moving along a circle and its linear velocity is 0.5ms when its angular velocity is 2.5rads−1. Its tangential acceleration is 0.2ms−2 then its angular acceleration is
View Solution

