A particle starts travelling on a circle with constant tangential acceleration. The angle between velocity vector and acceleration vector, at the moment when particle completes half the circular track. Is
zero
The correct Answer is:A
To solve the problem, we need to analyze the motion of a particle traveling along a circular path with constant tangential acceleration. We will determine the angle between the velocity vector and the acceleration vector when the particle completes half of the circular track.
1. Understanding the Motion:
- The particle is moving in a circular path with a constant tangential acceleration (denoted as aT).
- As the particle moves, it experiences two types of acceleration:
- Tangential acceleration (aT), which is responsible for changing the speed of the particle along the circular path.
- Centripetal acceleration (aC), which is directed towards the center of the circle and is responsible for changing the direction of the velocity vector.
2. Position at Halfway Point:
- When the particle completes half of the circular track, it will be at the point directly opposite its starting point on the circle.
- At this point, the velocity vector (→v) will be tangent to the circle and directed along the horizontal axis (assuming the starting point is at the top of the circle).
3. Direction of Accelerations:
- The tangential acceleration (aT) will also be directed along the tangent to the circle at the halfway point, which is in the same direction as the velocity vector.
- The centripetal acceleration (aC) will be directed towards the center of the circle.
4. Angle Between Velocity and Acceleration:
- Since the tangential acceleration (aT) is in the same direction as the velocity vector (→v), the angle between them is 0∘.
- The centripetal acceleration (aC) does not affect the angle between the velocity and tangential acceleration since it is always directed towards the center of the circle.
5. Conclusion:
- The angle between the velocity vector and the tangential acceleration vector when the particle completes half the circular track is 0∘.
Final Answer:
The angle between the velocity vector and the acceleration vector at the moment when the particle completes half the circular track is 0∘.
---
- The particle is moving in a circular path with a constant tangential acceleration (denoted as aT).
- As the particle moves, it experiences two types of acceleration:
- Tangential acceleration (aT), which is responsible for changing the speed of the particle along the circular path.
- Centripetal acceleration (aC), which is directed towards the center of the circle and is responsible for changing the direction of the velocity vector.
- When the particle completes half of the circular track, it will be at the point directly opposite its starting point on the circle.
- At this point, the velocity vector (→v) will be tangent to the circle and directed along the horizontal axis (assuming the starting point is at the top of the circle).
- The tangential acceleration (aT) will also be directed along the tangent to the circle at the halfway point, which is in the same direction as the velocity vector.
- The centripetal acceleration (aC) will be directed towards the center of the circle.
- Since the tangential acceleration (aT) is in the same direction as the velocity vector (→v), the angle between them is 0∘.
- The centripetal acceleration (aC) does not affect the angle between the velocity and tangential acceleration since it is always directed towards the center of the circle.
- The angle between the velocity vector and the tangential acceleration vector when the particle completes half the circular track is 0∘.
The angle between the velocity vector and the acceleration vector at the moment when the particle completes half the circular track is 0∘.
Topper's Solved these Questions
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Main (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:JEE Advanced (Archive)
Explore 19 Videos
- Motion in Two DimensionsBook:VMC MODULES ENGLISHChapter:Motion in Two DimensionsExercise:Long Answer Type
Explore 5 Videos
- Motion in Straight Line Book:VMC MODULES ENGLISHChapter:Motion in Straight Line Exercise:IN-CHAPTER EXERCISE-J
Explore 10 Videos
- MOVING CHARGES & MAGNETISM Book:VMC MODULES ENGLISHChapter:MOVING CHARGES & MAGNETISM Exercise:IN-CHAPTER EXERCISE-K
Explore 10 Videos
Similar Questions
Knowledge Check
Velocity vector and acceleration vector in a uniform circular motion are related as
Aboth in the same directionBperpendicular to each otherCboth in opposite directionDnot related to each other
A particle starts from rest and moves with constant acceleration. Then velocity displacement curve is:
View SolutionA particle starts from rest with constant acceleration. The ratio of space-average velocity to the time average velocity is :-
View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity ad acceleration vectors of point P is

View SolutionA disc of radius R is rolling purely on a flat horizontal surface, with a constant angular velocity. The angle between the velocity and acceleration vectors of point P is
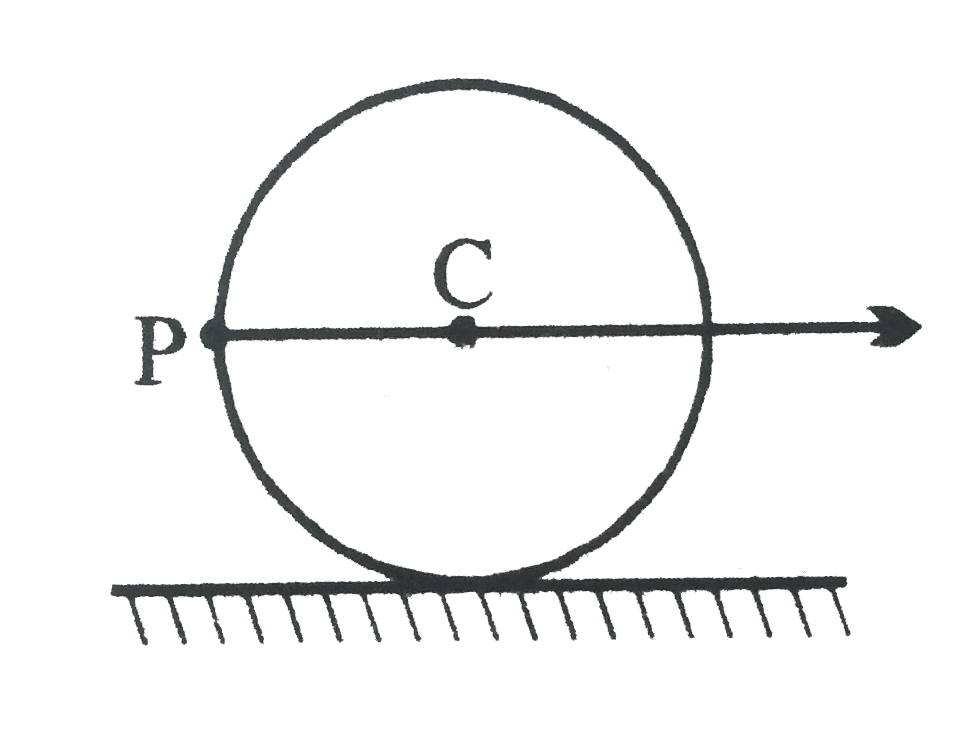 .
.
View SolutionIf a particle is moving on a circular path with constant speed, then the angle between the direction of acceleration and its position vector w.r.t. centre of circle will be
View SolutionAssertion:- A particle is moving in a circle with constant tangential acceleration such that its speed v is increasing. Angle made by resultant acceleration of the particle with tangential acceleration increases with time.
Reason:- Tangential acceleration =∣∣∣d→vdt∣∣∣ and centripetal acceleration =v2R
View SolutionA particle starts moving along a circle of radius (20/π)m with constant tangential acceleration. If the velocity of the parthcle is 50m/s at the end of the second revolution after motion has began, the tangential acceleration in m/s2 is :
View Solution

