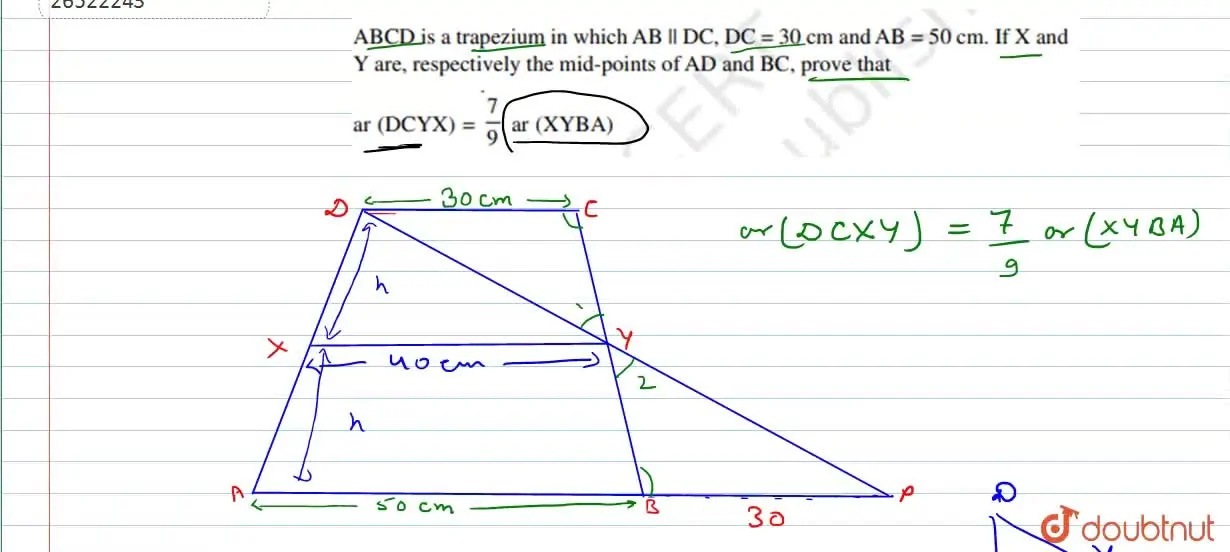
ABCD is trapezium in which AB∣∣DC, DC = 30 cm and AB = 50 cm. If X and Y are, respectively the mid-points of AD and BC, prove that
ar(DCYX)=79ar(XYBA).
Given In a trapezium ABCD, AB∣∣DC, DC = 30 cm and AB = 50 cm.
Also, X and Y are respectively the mid-points of AD and BC.
To prove ar(DCYX)=79ar(XYBA)
Construction Join DY and extend it to meet produced AB at P.
Proof In ΔDCY and ΔPBY,
CY=BY [since, Y is the mid-point of BC]
∠DCY=∠PBY [alternate interior angles]
and ∠2=∠3 [vertically opposite angles]
∴ ΔDCY≅PBY [by ASA congruence rule]
Then, DC=BP [by CPCT]
But DC=30cm [given]
∴ DC=BP=30cm
Now, AP=AB+BP
=50+30=80cm
In ΔADP, by mid-point theorem,
XY=12AP=12×80=40cm
Let distance between AB, XY and XY, DC is h cm.
Now, area of trapezium DCYX=12h(30+40)
[∵area of trapezium =12sum of parallel sides×distance between them]
=12h(70)=35hcm2
Similarly, area of trapezium=12h(40+50)=12h×90=45hcm2
∴ ar(DCYX)ar(XYBA)=35h45h=79
⇒ ar(DCYX)=79ar(XYBA) Hence proved.
Related Playlists
Similar Questions
ABCD is a trapezium in which AB || DC a and DC= 40 cm and AB = 60 cm. If X and Y a re respectively, the midpoints of AD and BC, then

XY=View SolutionABCD is a trapezium in which AB || DC, AB = 16 cm and DC = 24 cm. If E and Fare respectively the midpoints of AD and BC, prove that ar(ABFE) = 911 ar(EFCD).
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
 View Solution
View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
 View Solution
View SolutionIn the given figure ABCD is a trapezium with AB || DC. E and F are respectively midpoint of AD and BC. Prove that, EF=12(AB+CD)
 View Solution
View SolutionABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
View SolutionABCD is a square. E and F are respectively the mid-points of BC and CD. If R is the mid-point of EF, prove that ar(ΔAER)=ar(ΔAFR).
 View Solution
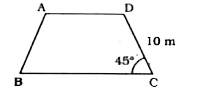
View SolutionABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
 View Solution
View SolutionABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
View SolutionABCD is a trapezium in which AB || DC, ABデ78 cm, CD = 52 cm. AD = 28 cm and BC =30cm . Find the area of the trapezium.
View Solution