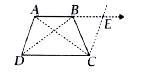
ABCD is a trapezium in which AD∣∣BC and AB=DC=10m. then the distance of AD from BC is :
10√2m
4√2m
5√2m
6√2m
The correct Answer is:C
Step by step video, text & image solution for ABCD is a trapezium in which AD||BC and AB = DC = 10 m. then the distance of AD from BC is : by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
90 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
70 Videos
- GEOMETRYBOOK - KIRAN PUBLICATIONCHAPTER - GEOMETRYEXERCISE - QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- X)
25 Videos
- DISCOUNTBOOK - KIRAN PUBLICATIONCHAPTER - DISCOUNTEXERCISE - Test Yourself
10 Videos
- LCM AND HCF BOOK - KIRAN PUBLICATIONCHAPTER - LCM AND HCF EXERCISE - Test Yourself
18 Videos
Similar Questions
Knowledge Check
ABCD is a cyclic trapezium with AD∣∣BC, If ∠A=105∘, then other three angles are
A∠B=75∘,∠C=75∘,∠D=105∘B∠B=105∘,∠C=75∘,∠D=75∘C∠B=75∘,∠C=105∘,∠D=75∘D∠B=105∘,∠C=105∘,∠D=75∘ABCD is a trapezium in which AB∣∣CD,AB=20cm,BC=10 cm, CD=10 cm and AD=10 cm . Find ∠ADC
A80∘B100∘C120∘D140∘Let ABCD be a trapezium in which AB||DC and E be the mid-point of AD. If F be a point on BC such that EF||AB. Then EF, where F is the mid-point of BC, is equal to
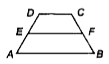 AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
AAB + DCB12(AB+DC)C13(AB+DC)DNone of these
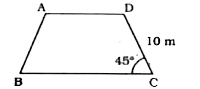
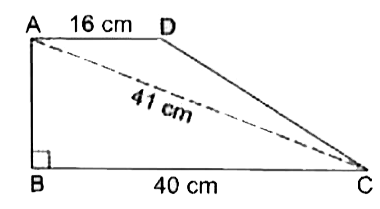
In the given figure, ABCD is a trapezium in which AD∣∣BC,∠ABC=90∘,AD=16cm,AC=41cm and BC = 40 cm. Find the area of the trapezium.
View SolutionABCD is a trapezium, in which AD||BC, E and F are the mid-points of AB and CD respectively, then EF is:
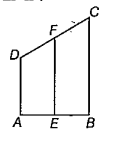
View SolutionIn the given figure. ABCD is a trapezium in which AB|| DC and E is the mid-point of AD, if EF||DC, then show that EF=12(AB+DC).
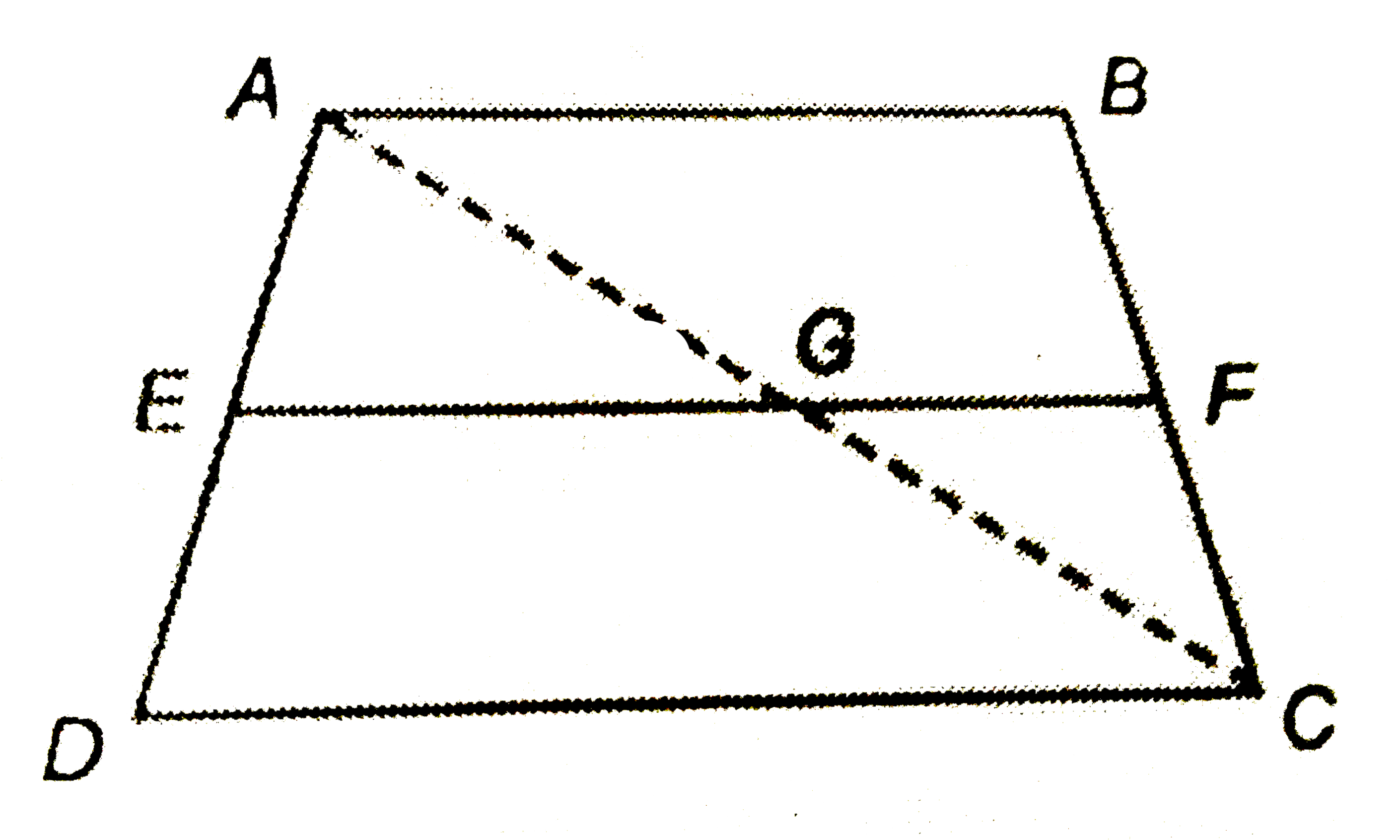
View SolutionABCD is a trapezium . AB ||CD and AB:CD=5:4, E and F are mid points of AD and BC, if CD= 20 cm , Find EF
View SolutionABCD is a trapezium , in which AD∣∣BC, E and F are the mid-point of AB and CD respectively , then EF is :
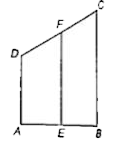
View Solution