AB is a diameter of circle with centre O. PQ is a chord which do not cut AB. If AP and BQ are joined. If ∠BAP=∠ABQ then ABQP is-
cyclic square
cyclic trapezium
cyclic rhombus
cyclic rectangle
The correct Answer is:B
Step by step video, text & image solution for AB is a diameter of circle with centre O. PQ is a chord which do not cut AB. If AP and BQ are joined. If angleBAP=angleABQ then ABQP is- by Maths experts to help you in doubts & scoring excellent marks in Class 14 exams.
Updated on:21/07/2023Topper's Solved these Questions
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XII)
Explore 90 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- XIII)
Explore 70 Videos
- GEOMETRYBook:KIRAN PUBLICATIONChapter:GEOMETRYExercise:QUESTIONS ASKED IN PREVIOUS SSC EXAMS (TYPE- X)
Explore 25 Videos
- DISCOUNTBook:KIRAN PUBLICATIONChapter:DISCOUNTExercise:Test Yourself
Explore 10 Videos
- LCM AND HCF Book:KIRAN PUBLICATIONChapter:LCM AND HCF Exercise:Test Yourself
Explore 18 Videos
Similar Questions
AB is the diameter of a circle whose centre is O. DC is a chord of that circle. If DC||AB and ∠BAC=20∘ then ∠ADC=?
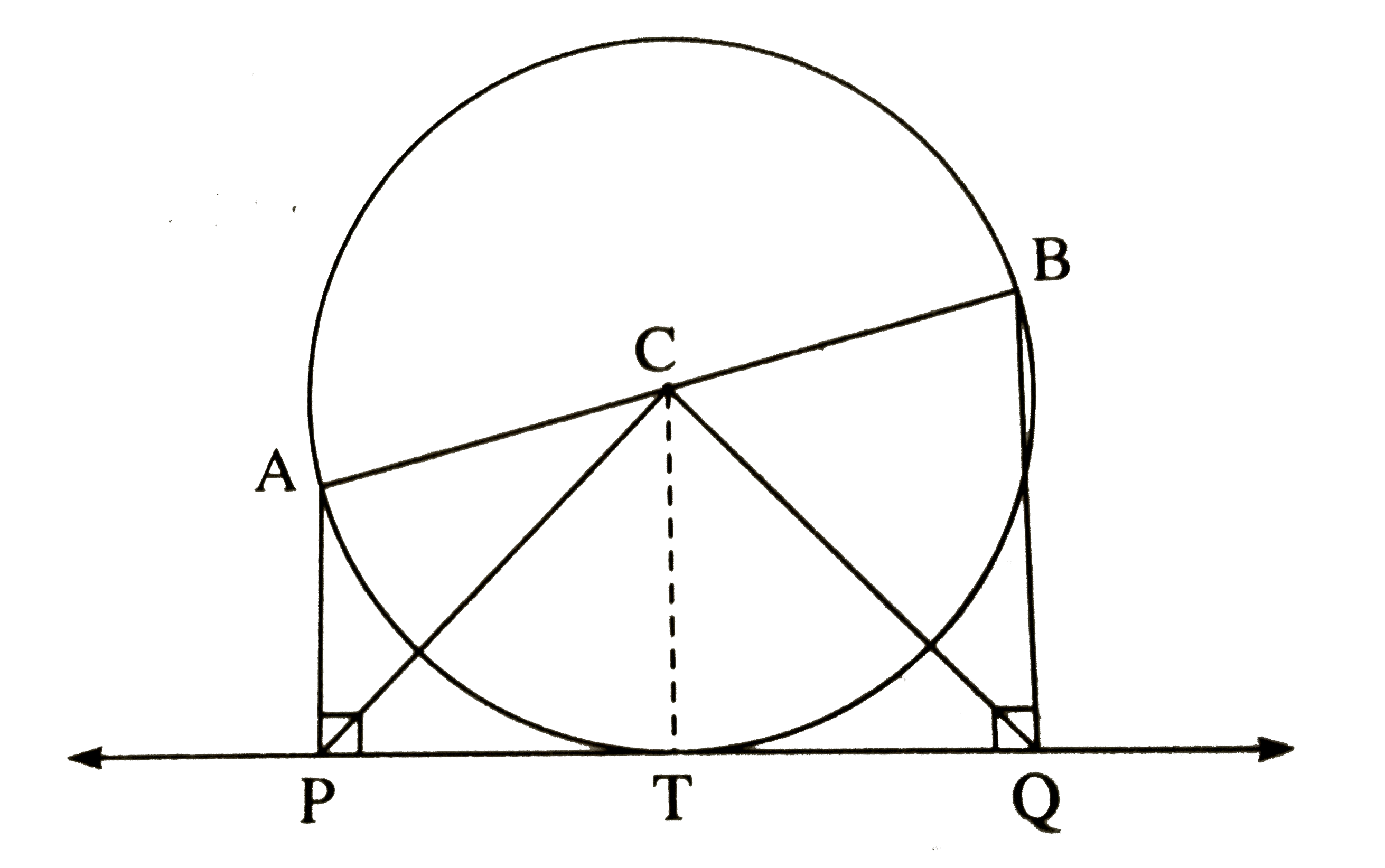
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
View Solution
Knowledge Check
AB is a diameter of circle with centre O. PQ is a chord which do not cut AB. If AP and BQ are joined. If ∠BAP=∠ABQ then ABQP is-
Acyclic squareBcyclic trapeziumCcyclic rhombusDcyclic rectangleAB is a diameter of a circle with centre O. CD is a chord equal to the radius of the circle. AC and BD are produced to meet at P. Then the measure of ∠APB is:
A120∘B30∘C60∘D90∘AB is a diameter of a circle with centre O, and P is a point on the circle. If ∠POA=130∘, the ∠PBO is equal to:
AB केंद्र O के साथ एक वृत्त पर एक व्यास है, और P वृत्त का एक बिंदु है। यदि ∠POA=130∘, तो ∠PBO का मान ज्ञात करे|A60∘B120∘C45∘D50∘
In the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.

View SolutionAB is the diameter of a circle which centre is O. DC is a chord where DC||AB. Accordingly if ∠BAC=20∘, then find the ∠COD.
View SolutionAB is a diameter of the circle with centre O, CD is chord of the circle. If ∠BOC=120∘, then the value of ∠ADC is
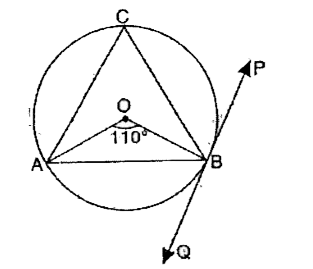
View SolutionIn the given figure, AB is a chord of the circle with centre O and PQ is a tangent at point B of the circle. If ∠AOB=110∘, then ∠ ABQ is
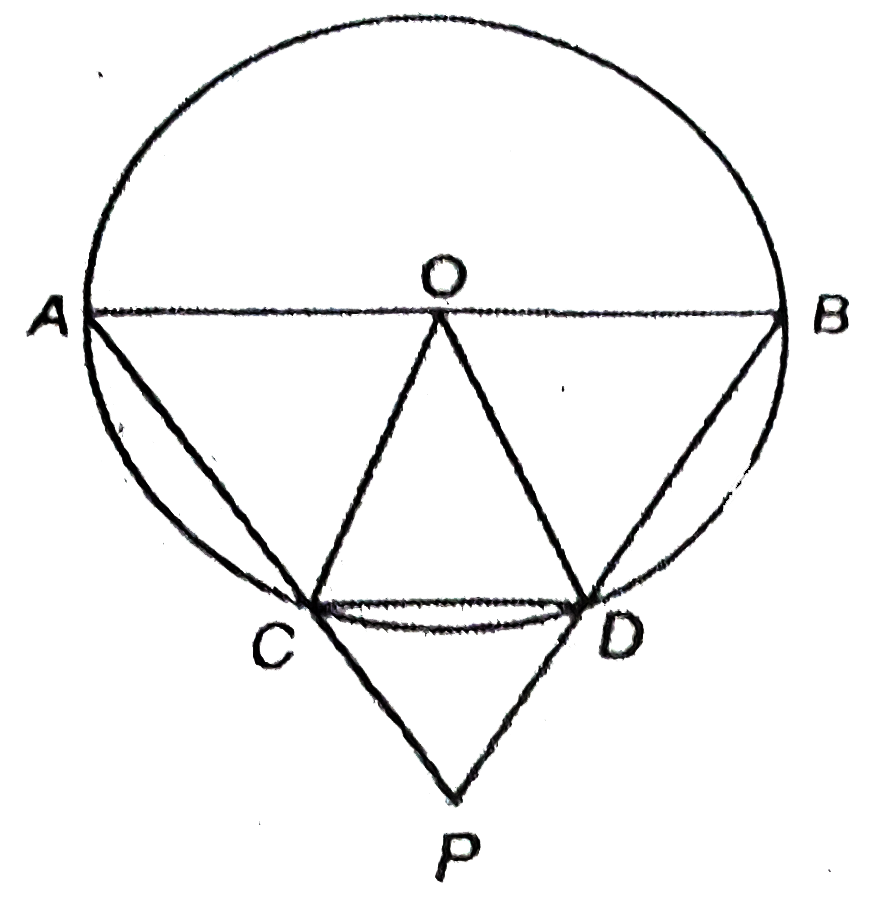
View SolutionAB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
View Solution
