A rigid bent light rod of total length 2l can slide on fixed wire frame with the help of frictionless sliders. There is thin liquid film (surface tension T) between bent rod and wire frame. In equilibrium the elongation in spring is given by (4Tlα5K). then find the value of α.
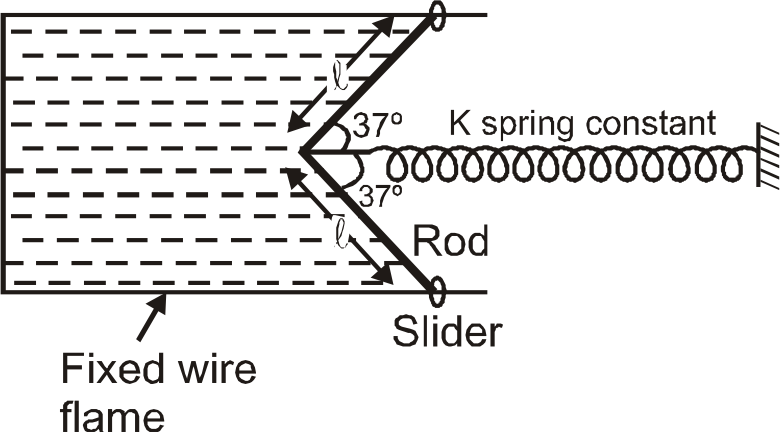
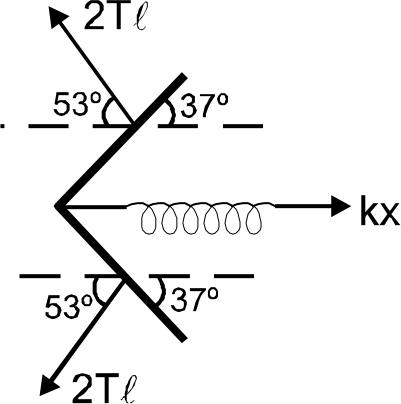
2(2Tl)cos53∘=Kx
4Tl35K=x
Topper's Solved these Questions
Similar Questions
AB is a massless frictionless glass rod which can slide on the U-frame XX', with the help of two frictionless rings. A water film is formed between the rod and the U-shaped frame. The rod is held in equilibrium by a hair- spring of stiffness k. Surface tension of water is T and length of rod AB is L. Find the extension in the spring.
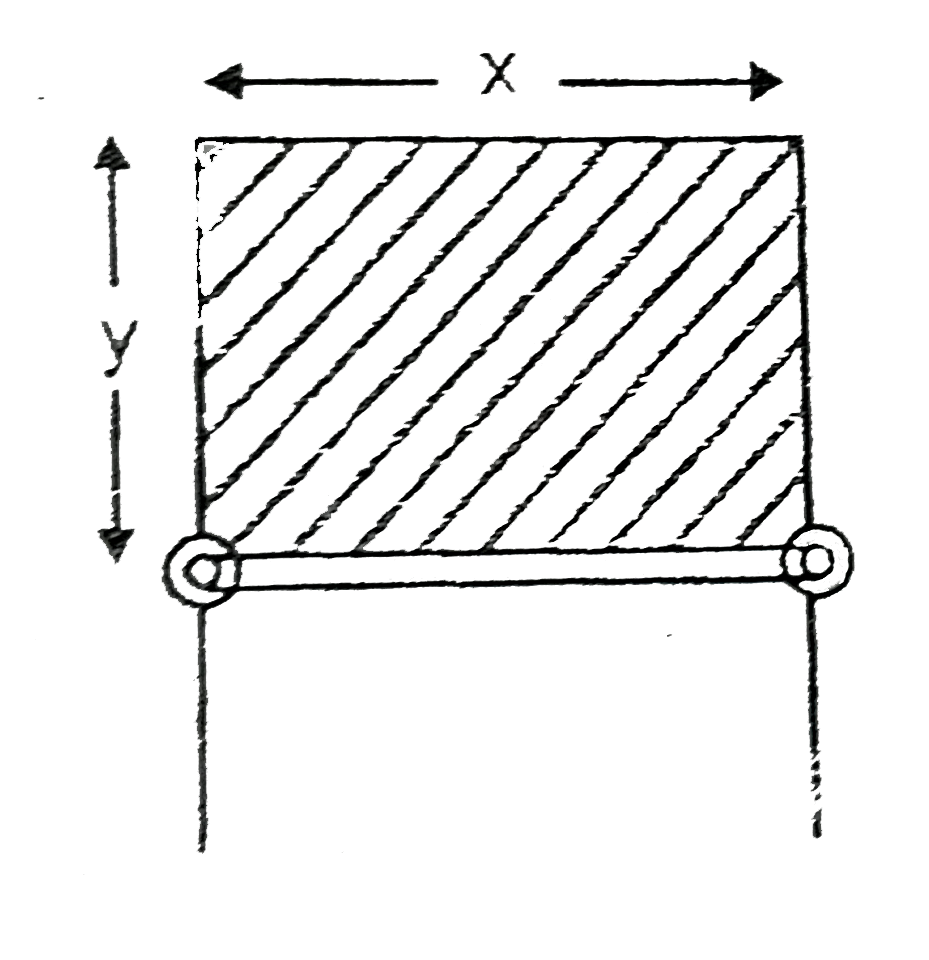
View SolutionBetween a frame and a light slider, a thin film of soap solution is made. Whose length is x and width is y. Find surface tension force on the slider. To keep the slider in equilibrium, how much weight should be suspended ?
View Solution
Knowledge Check
The surface tension of a thin liquid film formed between a U shaped wire and a light slider of length 30 cm supporing a weight of 1.5×10−2N is
 A0.0125Nn−1B0.1Nm−1C0.05Nm−1D0.025Nm−1
A0.0125Nn−1B0.1Nm−1C0.05Nm−1D0.025Nm−1A wire frame ABCD has a soap film. The wire BC can slide on the frame without friction and it is in equilibrium in the position shown in the figure. Find m, if T is the surface tension of the liquid.
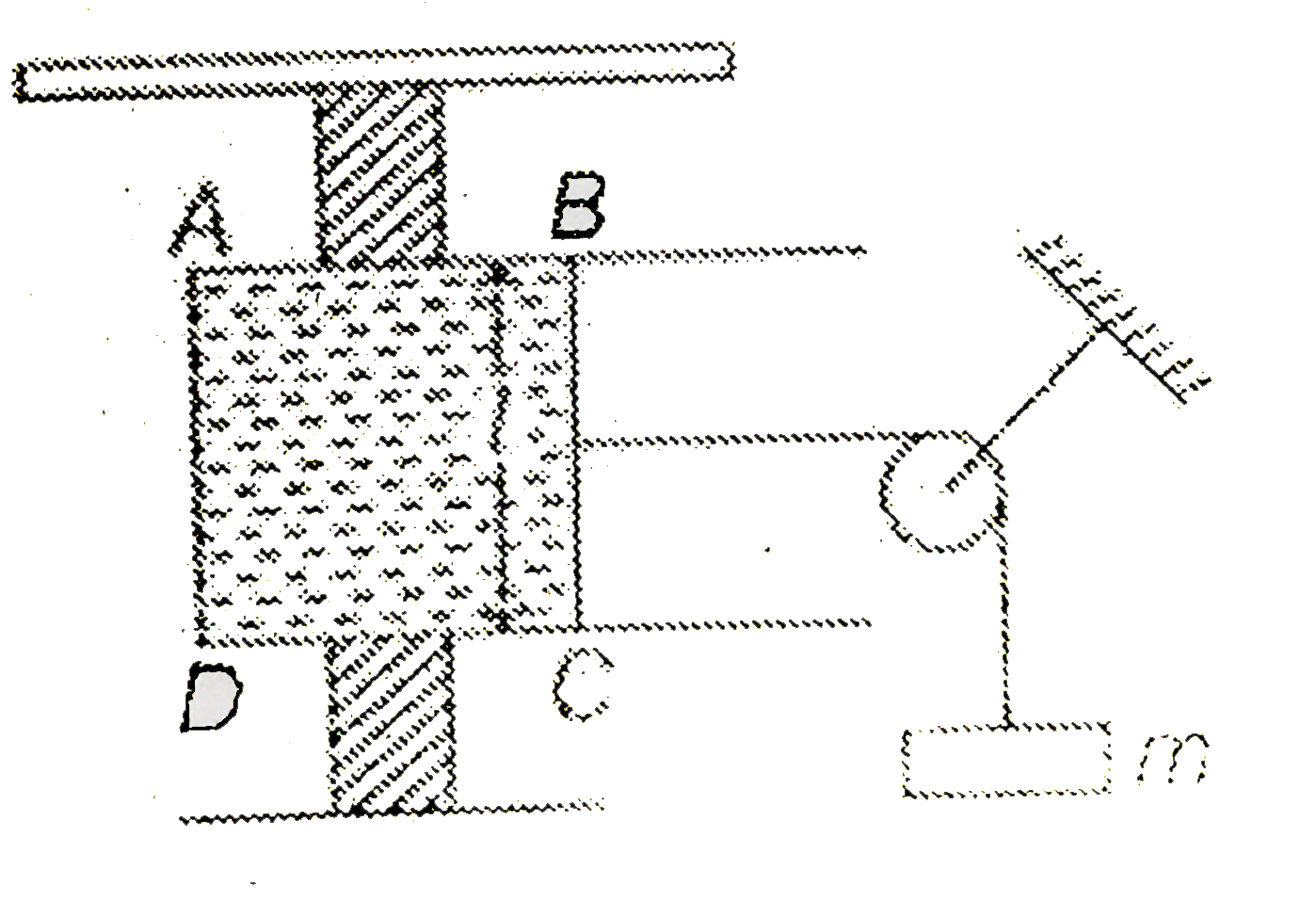 A2TlgBTlgCTl22gDTl2g
A2TlgBTlgCTl22gDTl2gThe surface tension of a thin liquid film formed between a U shaped wire and a light slider of length 30 cm supporing a weight of 1.5×10−2N is
 A0.0125Nm−1B0.1Nm−1C0.05Nm−1D0.025Nm−1
A0.0125Nm−1B0.1Nm−1C0.05Nm−1D0.025Nm−1
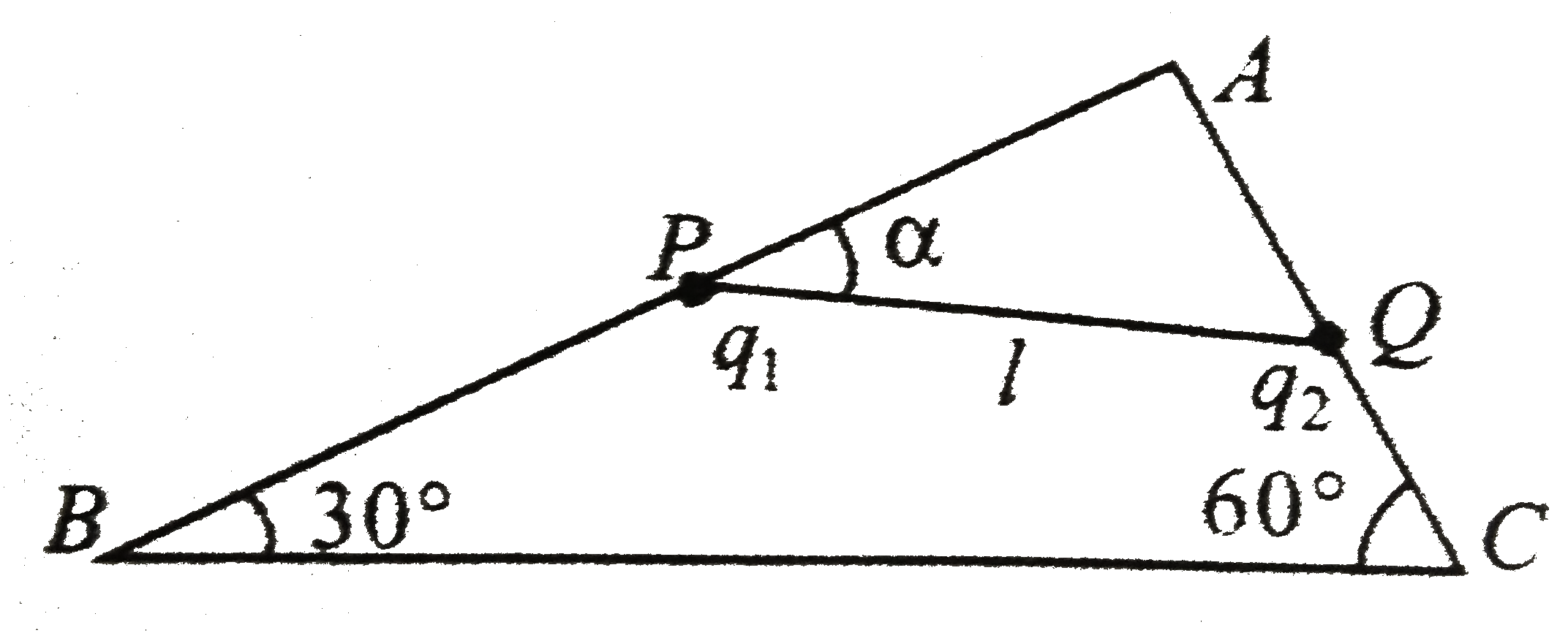
A rigeid insulated wire frame in the form of a right-angled traingle ABC is set in a vertical plane as shown in fig. two beads of equal masses m each and carrying charges q1 and q2 are connected by a cord of length l and can slide without friction on the wires.
Cinsidering the case when the beads are stationary, determine
(i) the angel α
(ii) the tension in the cord, and
(iii) The normal recation on teh beads.
If the cord is now cut, what are the value of the charges for which the beads continue to remain stationary?
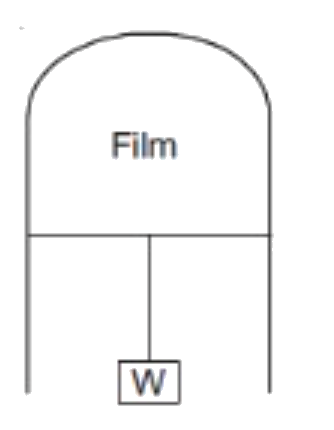
View SolutionA light wire AB of length 10 cm can slide on a vertical frame as shown in figure. There is a film of soap solution trapped between the frame and the wire. Find the load W that should be suspended from the wire to keep it in equilibrium. Neglect friction. Surface tension of soat solution =25dy≠cm−1.Takeg=10ms−2

View Solution
A wire is bent an an angle θ. A rod of mass m can slide along the bended wire without friction as shown in Fig. A soap film is maintained in the frame kept in a vertical position and the rod is in equilibrium as shown in the figure. If rod is displaced slightly in vertical direction, then the time period of small oscillation of the rod is
View SolutionA thin and light thread of sufficient length L is attached to a wire frame. The frame (along with the thread) is dipped into soap solution. When the frame is taken out of the solution, the thread takes the form of a semicircle with a soap film extending between the frame and the thread as shown in the figure (a). Now the thread is deformed into two semicircles by applying a force of F at the middle of the thread, as a result the film gets strectched as shown in the figure. (b). Calculate the surface tension of the soap solution.

View SolutionA uniform cylinder of mass m, length l and cross sectional area A is suspended with its vertical from a fixed point, with the help of a massless spirng of force constant (K), The cylinder is then submerged in a liquid of density p. At equilibrium the cylinder remains submerged in the liquid with 1/4th of its volume outside the liquid, as shown in the figure. The elongation of hte spring at this point is x0. WHen the cylinder is given a slight downward push into the liquid and then released, its starts oscillating with vertical S.H.M. of small amplitude.

The elongation X0 produced in the springs when the syste is in equilibrium is
View Solution

