The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
![The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation u=(3V)/2[1-(y/h)^(2)] where V is the mean velocity. The fluid has coefficient of viscosity eta Answer the following 3 questions for this situation. Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is](https://d10lpgp6xz60nq.cloudfront.net/physics_images/RES_DPP_PHY_07_E01_041_Q01.png)
where V is the mean velocity. The fluid has coefficient of viscosity Answer the following 3 questions for this situation.
Consider a rectangular cross section of dimensions l x 2h as shown. The side AB is parallel to the plates. Volume flow rate through this cross section is
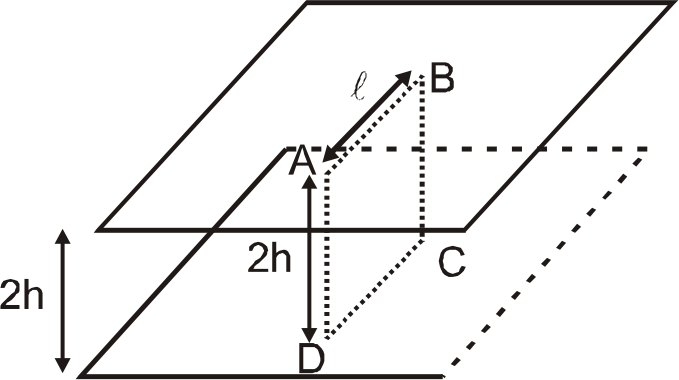
lhV/2
lhV
2lhV
3lhV
For this type of parallel flow the shearing stress is given as
For the given distribution
(a) Along the bottom wall so that (from eq. (ii))
and therefore the shearing stress is
(b) Along the plane where it follows from equation (ii) that
and thus the shearing stress is .
(C) 
Rate of volume flow
Topper's Solved these Questions
Similar Questions
The terminal velocity is________proportional to the coefficient of viscosity of the fluid.
View SolutionFind the dimensions of the quantity v in the equation,
v=πp(a2−x2)2ηl
where a is the radius and l is he length of the tube in which the fluid of coefficient of viscosity η is flowing , x is the distacne from the axis of the tube and p is the pressure differnece.
View Solution
Knowledge Check
The velocity distribution for the flow of a Newtonian fluid between two wide, parallel plates is given by the equation
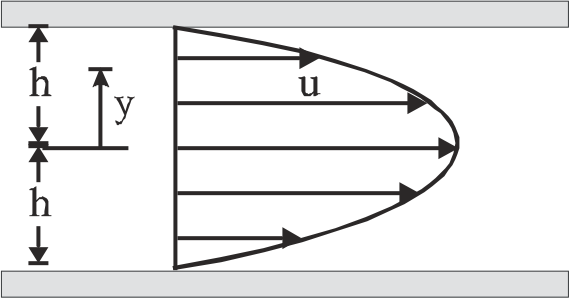
u=3V2[1−(yh)2]
where V is the mean velocity. The fluid has coefficient of viscosity η Answer the following 3 questions for this situation.
Shear stress acting on the bottom wall isAτbottom wall=η(3Vh)Bτbottom wall=η(3V2h)Cτbottom wall=η(6Vh)Dτbottom wall=η(Vh)For streamline flow of an incompressible fluid, If A is area and v is speed then equation of continuity is
AAv = constantBA+v= constantCAv= constantDvA= constantIf metal section of shape H is inserted in between two parallel plates as shown in figure and A is the area of each plate then the equivalent capacitance is.
 .AA∈0a−A∈0bBA∈0a+bCA∈0a+A∈0bDA∈0a−b
.AA∈0a−A∈0bBA∈0a+bCA∈0a+A∈0bDA∈0a−b
The critical velocity of the flow of a liquid through a pipe of radius 3 is given by vc=(Kηrp), where p is the density and η, is the coefficient of viscosity of liquid. Check if this relation is dimentionally correct.
View SolutionAn ideal fluid flows through a pipe of circular cross section with diameters 5 cm and 10 cm as shown. The ratio of velocities of fluid at A and B is

View SolutionFind the temperature distribution in a substance placed between two parallel plates kept at temperatures T1 and T2. The plate separation is l. The heat conductivity coefficient λ varies with temperature as 1/√T.
View SolutionAn ideal fluid flows through a pipe of circular cross - section with diameters 5 cm and 10 cm as shown in the figure. The ratio of velocities of fluid at A and B is

View SolutionThe coefficient of viscosity n of a fluid moving steadily between two surfaces is given by the formula, f=nAdVdx
where f is the frictional force on the fluid, A is an area in the fluid and dV/dx is the velocity gradient inside the fluid at that area. The SI unit of viscosity coefficient n is given as.
View Solution

