Radius of a nucleus is given by the relation R=R0A1/3 where R0=1.3×10−15m and A is mass number. For a nucleon inside a nucleus, de-Broglie wavelength is given by diameter of the nucleus. Average kinetic energy of a nucleon in the Te128 nucleus based on above information will be :
4.7 MeV
10 MeV
2 MeV
12 MeV
λ=2R=2R0A1/3
P=hλ⇒E=P22m=h22m(4R20A2/3)
E=(6.62×10−34)22×1.67×10−27×4(1.3×10−15)2(128)2/3 joule
=4.72 MeV.
Topper's Solved these Questions
Similar Questions
from the relation R=R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A ).
View SolutionFrom the relation R=R0A13, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A).
View Solution
Knowledge Check
The radius of a nucleus is given by r0A1/3 where r0=1.3×10−15 m and A is the mass number of the nucleus, the Lead nucleus has A = 206. the electrostatic force between two protons in this nucleus is approximately
A102 NB107 NC1012 ND1017 NIf there are N nucleons in a nucleus of radius R, then the number of nucleons in a nucleus of radius 2R will be :
ANB2NC8ND21/3NRead the following passage carefully and answer the questions
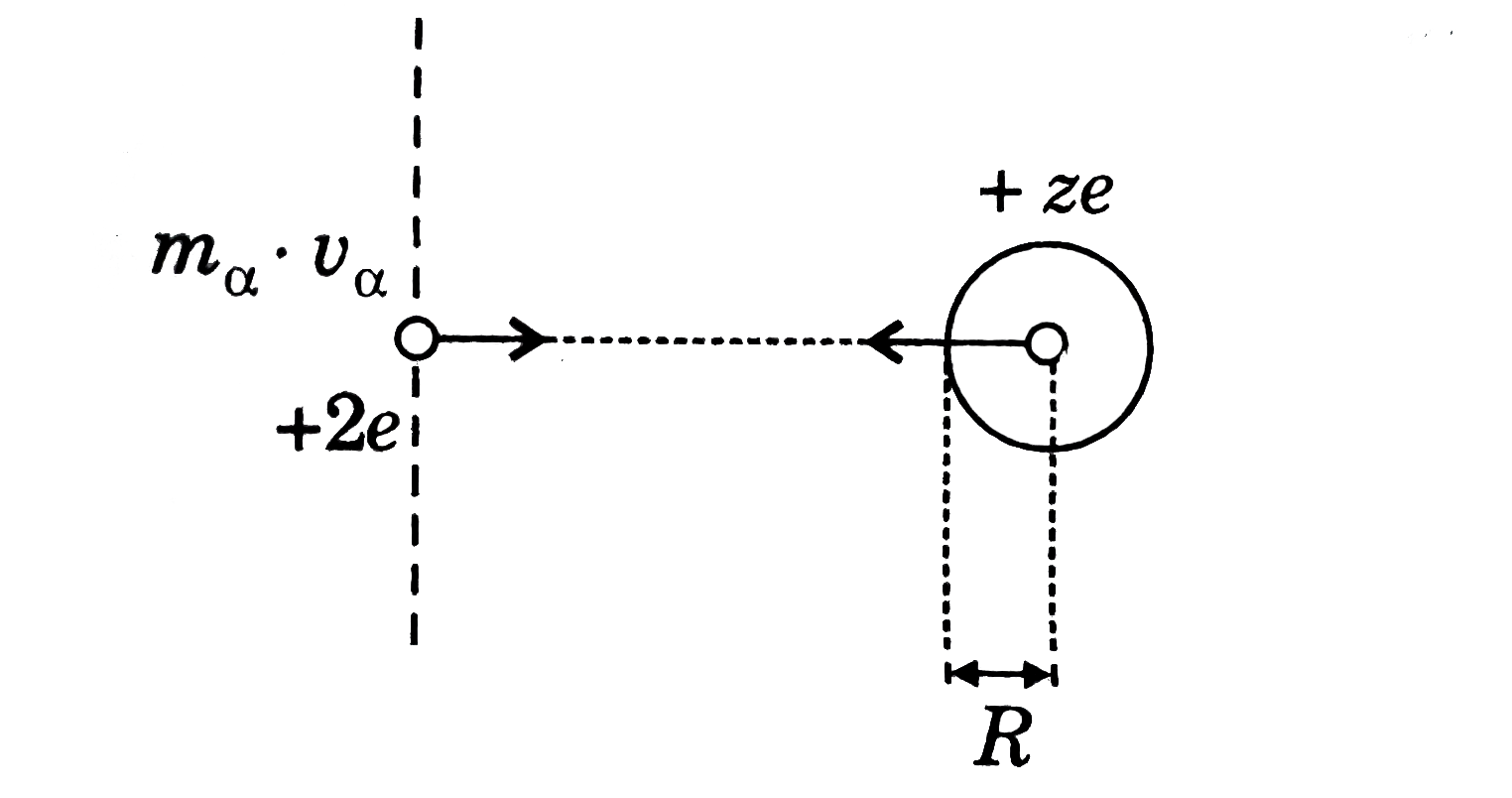
The approximate size of the nucleus can be calculated by using energy conservation theorem in Rutherford's α−scattering experiment. If an α−perticle is projected from infinity with speed v, towards the nucleus having z protons then the apha−perticle which is reflected back or which is deflected by 180∘ must have approach closest to the nucleus. It can be approximated that α−particles collides with the nucleus and gets back. Now if we apply the energy conservation at initial and collision point then:
(Total Energy)initial=(Total Enregy)final
(KE)i+(PE)i=(KE)f+(PE)f
(PE)i=0,sincePE of two charge system separated by infinite distance is zero, finally the particle stops and then starts coming back.
12mαv2α+0=0+kq1q2R
⇒12mαv2α=k2e×zeR⇒R=4kze2mαv2α
Thus the radius of nucleus can be calculated using above equation. The nucleus is so small a particle that we can't define a sharp boundary for it . Experiments show that the average radius R fo a nucleus may be written as
R=R0(A)1/3
where R0=1.2×10−15m
A= atomic mass number
R=radius of nucleus
If α−particle with speed v0 is projected from infinity and it approaches upto r0 distance from the nuclei. Then the speed of α−particle which approaches 2r0 distance from the nucleus isA√2v0Bv0√2C2v0Dv02
form the relation R=R0A1/3, where R0 is a constant and A is the mass number of a nucleus, show that the nuclear matter density is nearly constant (i.e., independent of A ).
View SolutionAssuming the radius of a nucleus to be equal to R=1.3A1/3×10−15m. Where A is its mass number, evaluate the density of nuclei and the number of nucleons per unit volume of the nucleus. Take mass of one nucleon =1.67×10−27kg
View SolutionThe radius of nucleus is r=r0A1/3, where A is mass number. The dimensions of r0 is
View SolutionThe radius of a nucleus ofa mass number A is given by R=R0A1/3, where R0=1.3×10−15m. Calculate the electrostatic potential energy between two equal nuclei produced in the fission of .23892U at the moment of their fission
View SolutionCalculate the radius of oxygen nucleus. Take R0=1.1×10−15mandA=16
View Solution

