A cubical block of mass m and surface area 6A is placed on a thick layer of viscous liquid, of thickness d as shown

Initially the block is at rest. A constant horizontal force F0 starts acting on the block at t = 0. In column - 1 a physical quantity regarding the motion of the block is given and in column-2 corresponding variation with time is given. Match the proper entries from column-2 to column-1 using the codes given below the columns.
Column-IColumn-II(P) X (distance travel by the block as function of time.) (1)αe−βt(α,β≠0)(Q) V (velocity of block as as function of time.)(2)α+βt+γe−δt(α,β,γ,δ≠0)(R) A (acceleration of block as as function of time.)(3)αe−βt−γe−δt(α,β,γ,δ≠0)(S) dK/ dt (rate of change in kinetic energy of block as as function of time.)(4)α+βeγt(α,β,γ≠0)
(here α,β,γ,δ may have different values in each of options)
PQRS(A)2134
PQRS(B)2413
PQRS(C)2431
PQRS(D)1243
F=mA=F0−Fv=F0−ηAvd
A=F0m−ηAmdv=a−bv
dvdt=a−bv⇒∫v0dva−bv=∫t0dt
⇒(−1b)ln(a−bva)=t⇒V=ab(1−e−bt)
dxdt=ab(1−e−bt)⇒∫x0dx=ab∫t0(1−e−bt)dt
x=abt−ab2+ab2e−bt
A=ae−bt
k=12mv2
dkdt=mvdvdt=mab(1−e−bt)(ae−bt)=ma2b(e−bt−e−2bt)
Topper's Solved these Questions
Similar Questions
A block is placed on a rough horizontal surface. A constant force F is acting on the block as shown in the figure.
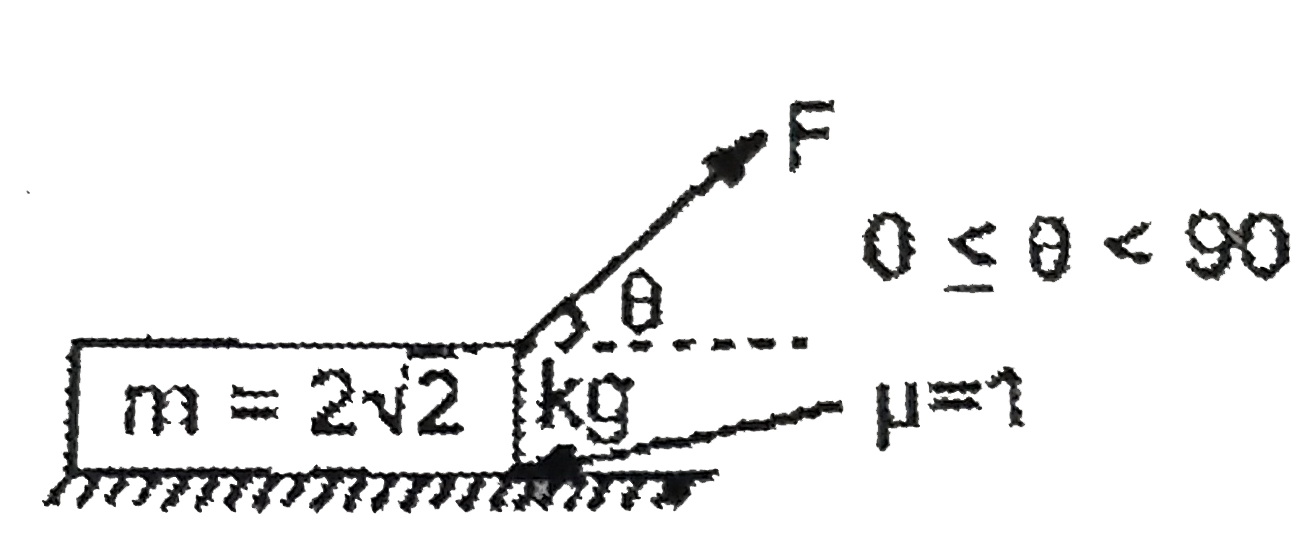
Column-1 gives the magnitude of force F and column-2 gives information about friction acting on the block. Match the entries in column-1 to all possible entries in column-2.
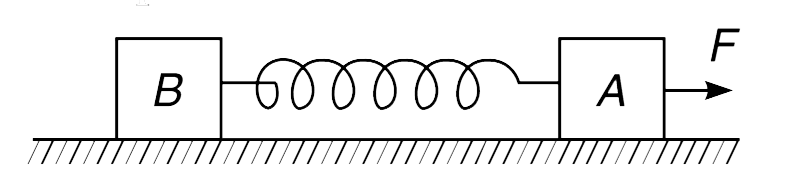
View SolutionTwo blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
View Solution
Knowledge Check
A force of 50N acts in the direction as shown in figure. The block of mass 5kg, resting on a smooth horizontal surface. Find out the acceleration of the block.
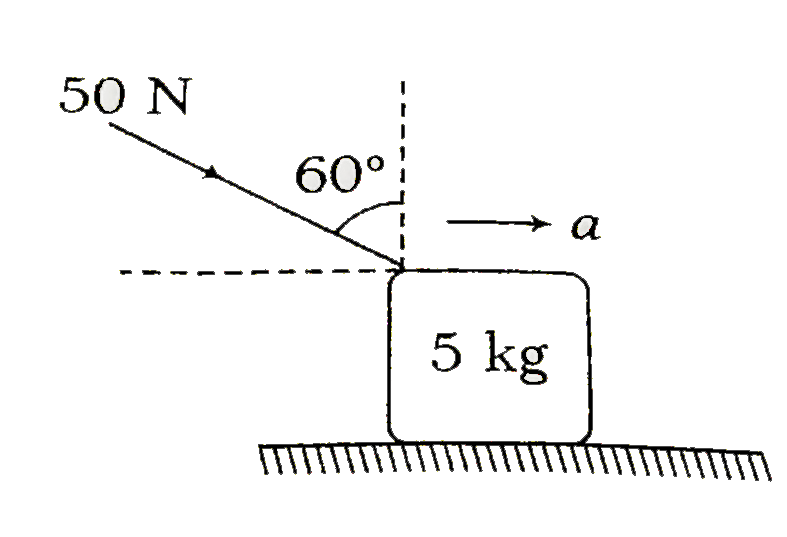 A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2
A5√3ms−2B2√3ms−2C15√3ms−2D3√3ms−2In the figure shown, all surfaces are smooth and the pulley is massless. A constant force of magnitude F=mg2 is acting on the block of mass M. The acceleration of the block M is :
 Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward left
Amg2(m+M) towards rightBmg2(m−M) towards rightsCmg2(m−M) towards leftDmg2(m+m) toward leftA block is kept on a rough horizontal surface as shown. Its mass is 2 kg and coefficient of friction between block and surface (μ)=0.5. A horizontal force F is acting on the block. When
 AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
AF = 4 N, acceleration is zero.BF = 4 N, friction is 10 N and acceleration is 3m/s2.CF = 14 N, acceleration is 2m/s2.DF = 14 N, friction is 14 N.
A block is placed on a smooth inclined plane as shown . For what value of horizontal force F, the block will remain at rest ?

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied on a 1-kg block. Find the force of interaction of the blocks.

View SolutionA block is placed on a rough horizontal plane. A time-dependent horizontal force F=kt2 acts on the block. Here k is a positive constant. Acceleration -time graph of the block is
View SolutionA horizontal force F acts on the block of mass m and the block remains stationary, thr value of friction force is.

View SolutionA block of mass m is connected to another block of mass M by a spring (massless) of spring constant k. The block are kept on a smooth horizontal plane. Initially the blocks are at rest and the spring is unstretched. Then a constant force F starts acting on the block of mass M to pull it. Find the force of the block of mass M.
View Solution

