Two blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ?
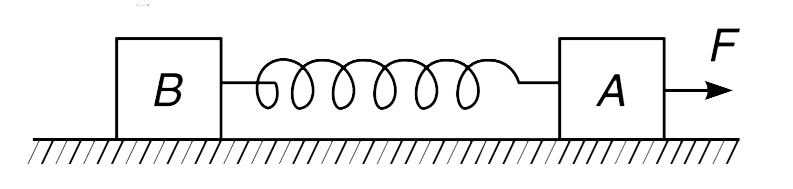
The correct Answer is:Ft24m+l2
Step by step video, text & image solution for Two blocks A and B, each of mass m, are connected by a spring of force constant K. Initially, the spring is in its natural length. A horizontal constant force F starts acting on block A at time t=0 and at time t , the extension in the spring is seen to be l. What is the displacement of the block A in time t ? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Initially block shown is at rest and the spring is unstretched, when a constant force F begins to act on it neglect friction. Find
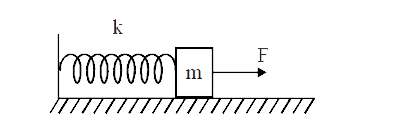
maximum extension in the spring
View SolutionTwo blocks rest on a smooth horizontal surface. They are connected by a spring of force constant k. If the system is set into oscillation find its time period.

View Solution
Knowledge Check
Two blocks of mass m and 2m are kept on a smooth horizontal surface. Theya are connected by an ideal spring of force constant k. Initially the spring is unstretched. A constant force is applied to the heavier block in the direction shown in figure. Suppose at time t displacement of smaller block is x1 then displacement of the heavier block at this moment would be
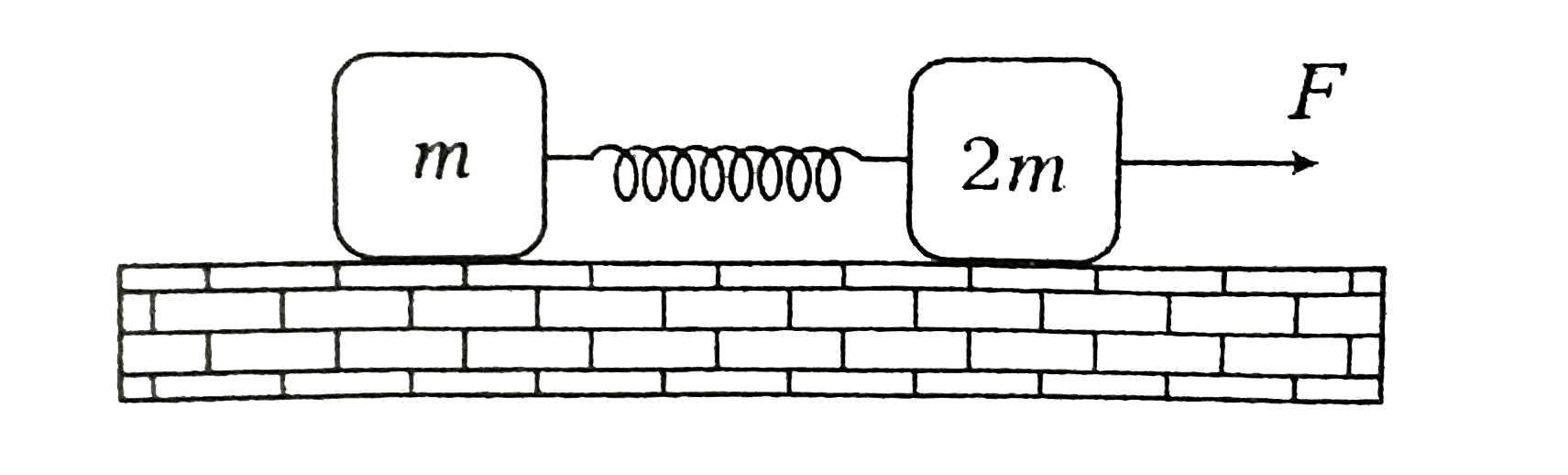 Ax2BFt26m+x3Cx3DFt24m−x2
Ax2BFt26m+x3Cx3DFt24m−x2Two blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
AF=μ(m1+m22)gBF=μ(m12+m2)gCF=μ(m21+m222)gDF=μ2(m21+m22)gTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the first block at this instant isA12(Ft22m+x0)B−12(Ft22m+x0)C12(Ft22m−x0)DFt22m+x0
Two blocks of masses m and M connected by a spring are placed on frictionless horizontal ground. When the spring is relaxed, a constant force F is applied as shown. Find maximum extension of the spring during subsequent motion.
View SolutionTwo blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionA block of mass m is connected to another .block of mass M by a massless spring of spring constant k. A constant force f starts action as shown in figure, then:

View SolutionTwo blocks of equal mass m are connected by an unstretched spring and the system is kept at rest on a frictionless horizontal surface. A constant force F is applied on the first block pulling away from the other as shown in Fig.

If the extension of the spring is x0 at time t, then the displacement of the second block at this instant is
View SolutionA block of mass m is connected to a spring (spring constant k). Initially the block is at rest and the spring is in its natural length. Now the system is released in gravitational field and a variable force F is applied on the upper end of the spring such that the downward acceleration of the block is given as a=g−αt, where t is time elapses and α=1m/s2, the velocity of the point of application of the force is:
View Solution
